基于图像的非真实感艺术绘制技术综述

钱小燕

（南京航空航天大学民航学院，江苏 南京 210016）

非真实感绘制（Non-photorealistic Rendering,NPR）是计算机图形学和图像处理中一个崭新的课题，属于计算机艺术的范畴。NPR是计算机科学与艺术的有效融合，以计算机为工具，搭建各种数学模型并设计各种算法，来模拟艺术式的绘制风格。主要目的是将某个对象以简洁、含蓄、带有美学特征的方式借助计算机表现出来，也即能在形式上指定一种可展现绘画作品的方式并随之编写生成非真实感绘画作品的计算机程序[1-3]。

目前，非真实感绘制技术已经能够实现多种艺术作品的模拟创作，如：水彩画、各种风格的油画、中国画、点画等；在计算机动画制作中也有了广泛的应用，它不仅能够实现动画数据作为运动图像的可视化，也可实现其作为静态图像的可视化；非真实感绘制与计算机辅助建筑设计结合，在建筑业也获得了重要的应用，它们的结合不但可以向用户展示未来环境中的建筑物，而且可以利用虚拟现实技术进行场景设置，使人们能够在建筑物建好之前就可以“访问”它；另外，在医学领域，非真实感绘制技术可实现医学数据的可视化；还可实现针对盲人的触觉绘制等。

基于图像空间的非真实感艺术绘制工作可分为两类：一类是计算机自动绘制生成所需的艺术风格图像，典型算法包括颜色传输和基于纹理合成的艺术风格传输。另一类是基于过程的物理模拟，即基于画笔的非真实感艺术绘制。它通过抽象出特定的笔刷模型，使之产生与现实绘画工具相似的艺术效果。下面进行分类描述。

1 颜色传输算法

在NPR中，为了获得特定的艺术效果，绘制效果的颜色往往是需要考虑的一个重要方面。比如，把一幅普通照片渲染成油画风格，由于照片颜色可能比较单一，导致整个绘制画面颜色比较呆板、缺乏生气，而不能达到油画般丰富的颜色效果，需要对其进行颜色渲染，增强其颜色效果。有多种方式可以改变图像的颜色，其基本形式可以用变换T表示：，其中，分别表示变换后的图像和源图像；T可以是滤波器，也可以是一个映射或函数关系。近几年来，统计学已经广泛应用于视觉信息处理，将T理解为把源图像的统计信息传输至目标图像是一个全新的思路，也就是颜色传输技术。它有效利用了图像的基本统计信息，变换目标图像的统计信息，使之与样本图像具有相似的统计分布，从而使得两幅图像具有类似的颜色特征，达到颜色传输的目的。

1.1 全局颜色传输算法

为了体现颜色空间中的不同特性，人们总结了很多颜色空间模型，但许多颜色空间关联性都比较强，当编辑图像的时候，常常需要对像素的3个分量同时修改才不会影响图像本身具有的自然效果。Ruderman等[4]提出了一种更适合于人类视觉感知系统的空间-ιαβ颜色空间的概念，并给出一个简单的3×3的矩阵把RGB空间的向量转换到ιαβ空间，其中，ι表示非彩色通道；α表示黄-蓝通道；β表示红-绿通道。这一空间的3个通道相互正交，对于自然场景，通道间的相关性降到了最小。Reinhard等[5]把这个空间应用到颜色传输中，提出了全局颜色传输的概念。利用图像的全局统计特征，对目标图像的3个通道分别进行修改，使其具有类似于源图像的统计特征。这一算法对具有单颜色基调图像的处理比较成功，但对多颜色基调的图像却不能获得自然、真实的传输效果。

1.2 基于高阶矩的颜色传输算法

全局颜色传输算法仅将图像视为二阶过程，但人们通过从单个属性的边际分布和多个属性的联合分布的形状中得出的结论是：图像具有较高的峰值，仅仅假定其为二阶过程是不够的。这一发现改变了人们一味地走传统高斯分析的路子，转而更多地从图像中捕获高阶信息。赵国英等[6]利用幂变换和模变换对源数据的斜度和峰度等高阶矩进行调整，使之类似于样本图像的分布，再结合全局颜色传输使得绘制效果的整体光照或部分光照更加类似于样本图像的特征，从而使得传输效果得到了进一步的改善。

1.3 分而治之的颜色传输

将图像的峰度和斜度等高阶信息引入颜色传输中，虽然对全局颜色传输算法有所改进，但对相似性较差或包含多个不同颜色区域的图像仍不能获得自然的传输效果。主要原因在于没有能够提供传输过程中所需的足够的空间信息，当源图像或目标图像包含多个不同颜色区域时，不能有效分辨出这些区域包含的不同统计信息，从而导致混合传输，形成不自然的传输效果。就这一问题，Reinhard等[5]提出了一种分而治之的解决方法：从两幅图像中取出代表不同对象的若干块，选择对应的颜色传输块，对应块间采用全局颜色传输的思想进行颜色传输。但该方法仍没能提供足够的分区信息，也没能给出对应块的选择标准。

针对以上问题，文献[7]在以往颜色传输算法基础上，把模糊C-均值聚类算法应用到颜色传输中，提出了一种基于模糊C-均值颜色聚类的颜色传输算法：利用模糊颜色聚类思想把源图像和目标图像分成若干包含不同颜色特征的聚类域；为了获得匹配域，为每个聚类域设置一个匹配权值参数，根据目标图像的特征采用不同的权值计算方法；然后根据目标图像中的匹配权值在源图像中选取一个与之最接近的域作为匹配域；最后在颜色传输过程中，引入隶属度因子对各聚类域的处理结果进行平滑，解决图像中存在不确定性信息的情况。与以往颜色传输算法相比，基于模糊C-均值颜色聚类思想的颜色传输算法能够获得更加和谐、自然的传输效果。对于相似性较差的图像，利用模糊聚类的思想，能够获得更加有效的分区；通过匹配权值获得有效的对应模块，能够使得传输效果更加自然，真实。

图1给出了各种颜色传输算法的实验效果，目的是将源图像图1(a)的颜色特征传输至目标图像图1(b)。图1(c)直接应用全局颜色传输算法，整个画面被一层淡淡的黄色笼罩，但树叶、树干等都呈现出不真实的黄色。图1(d)经高阶矩调整后，获得了更加明亮、清晰的传输效果，但也不能很好地避免失真情况。但图1(c)、(d)能呈现出一种陈年老照片的艺术感。图1(e)为应用模糊C-均值颜色聚类的颜色传输算法的传输效果。可以看出，图1(e)较好地继承了源图像中各域的颜色特征，树木、天空等仍保持了比较真实、自然的颜色效果，整个画面更加清晰，更加接近目标图像的颜色分布。

图1 各种颜色传输算法的传输效果

2 基于纹理合成的艺术风格传输

应用纹理合成技术生成具有特定艺术风格的图像是基于图像的非真实感艺术绘制的一个重要方面。这种技术不像基于物理过程的绘制，需要对各种手绘风格图像的特征进行比较深入的研究和分析，并需要较多的交互工作，对不熟悉绘画的用户，要调试出具有较好视觉效果的风格画很不容易。基于纹理合成的非真实感艺术绘制仅需设定与纹理合成相关的参数便可自动把手绘图像的风格传输至目标图像，使得目标图像具有与源图像类似的艺术风格。

应用纹理合成技术实现两幅图像间的艺术风格传输的工作仍不是很多。Hertzmann等[8]提出了一种基于类推思想的绘制算法，可以将绘画风格传输到新的实例中。为了获得具有画家本人风格特点的绘制效果，该算法需要一对源图像A，A′和一幅目标图像B′，其中A是A′的原始参考图像。算法通过学习源图像间纹理合成的方法，再将这一方法类推到目标图像中，从而生成类似于源图像艺术风格的图像。当原始参考图像无法获得时，文献[8]采用了对A′滤波的方法得到A，虽然这种方法具有较大的随机性，不易控制A的调整程度，但仍可获得比较好的类比效果。徐文华等[9]将纹理合成算法应用在敦煌壁画虚拟的复原临摹工作中，取得了较好的效果。文献[8]和文献[9]都采用两种搜索方法来寻找待选点：逼近搜索获得全局最优的匹配点，经典Ashikhmin算法[10]获得邻域相关的待选点。综合运用这两种方法虽然能够获得不错的风格传输效果，但为了获得一个匹配点，逼近搜索需要上万次的迭代，并且源图像分辨率愈高，迭代次数越多；而Ashikhmin算法也需要几十次的计算才能获得一个待选点。因此，为了获得最终传输效果，需要花费几十分钟甚至一小时的时间。

逼近搜索和Ashikhmin算法都以L2距离作为相似性度量，而此方法是个不完美的概念性相似度量方法，潜在的平滑高斯模型往往使得合成效果比较模糊，因此需要寻求更好的度量方法来获得最佳匹配点。文献[11]以经典Ashikhmin算法为基础并对其进行改进，提出了一种新的邻域一致性度量方法，把源图像和目标图像及其低频图像的统计特性引入相似性度量中，提高了匹配点搜索的效率。此文献还以随机产生待选点的方法扩大搜索范围，同时采用双向扫描方法进行风格传输，解决了Ashikhmin 算法易产生纹元不完整的情况，以及绘制效果中存在可察觉水平边缘的现象，从而获得了理想的风格传输效果，且收敛速度也大大提高（图2所示将一幅水杉图片渲染成斑驳效果）。

图2 斑驳艺术风格传输效果[11]

3 基于画笔的非真实感绘制

基于画笔的绘制（stroke-based rendering,SBR）一直是基于图像的非真实感艺术绘制的重点。不像基于纹理合成的艺术风格传输，仅能较好地实现自然纹理间的风格传输，基于画笔的非真实感艺术绘制可以通过控制画笔的颜色、形状、方向等元素产生各种艺术风格，如：素描、水彩画、油画、pen-and-ink等风格。这种方法通常模拟画家的真实创作过程，形成手绘风格图像。设计SBR算法有两类方法：贪婪算法和最优化算法：贪婪算法为了与目标目的匹配，贪婪地放置画笔；最优化算法[12]通过交互地放置画笔，然后调整画笔以使得目标函数最小。

3.1 基于最优化算法的SBR

到目前为止，已经有两类最优化算法应用到SBR中：一类是Voronoi算法，另一类是trial-anderror算法。Voronoi算法的中心思想是：应用有效的计算几何技术控制画笔的密度分布，使得一组不相重叠的画笔最终能够均匀分布到图像中。应用最优化算法设计SBR程序需要定义能量函数：记p(x,y)代表图像中像素点位置，ci是质点，也就是画笔最终所在位置；为标记位，表示点p是否属于质点ci，最优化程序归结为能量函数E(I)的最小化问题

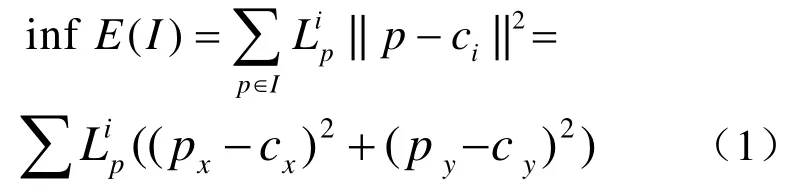
Voroni图[13]可以使得各质点拥有一组与它最近的像素点，但无法使得质点分布达到最优。Lloyd方法[15]对Voroni图作了改善，通过迭代均值化计算获得一组质点集，使质点能够均匀分布在图像中，从而使得能量函数最小。

以Lloyd方法为基础，Deussen等[14]首先提出了近似目标图像灰度分布的点画算法。先把图像分成几个相区别的区域，用半色调算法初始化质点；然后应用Lloyd方法确定质点位置，获得一组均匀分布的质点；最后用点画（Stipples）代替这些质点。为了体现图像灰度变化，点画大小与目标图像中对应位置处灰度值成比例。后来，Secord[13]又提出了Stipples风格可以选择的算法，定义一个密度函数来决定图像不同区域Stipples的分布情况，用Stipples之间的空间变化代替了大小变化。

Lloyd方法[15]也可用来形成瓦片拼接（tile mosaics）效果。只需根据源图像对应位置颜色对Voroni图各区域进行着色，便可产生瓦片拼接效果。但无法产生大小和形状都很规则的瓦片（tile）。后来，Hausner[16]对此方法做了两点改进：一是用L1距离代替L2距离产生规则的方形瓦片；二是给图像建立一个方向域，使得瓦片能够按照特定的方向放置，这个算法中能量函数修正为

Voroni算法很难考虑颜色信息，也无法处理画笔重叠问题。trial-and-error算法能较好地解决这些问题。这一算法建议对图像结构进行修改，如果修改后能够降低能量函数，那么就采纳这一修改建议，否则忽略。Haeberli[17]首次把trial-and-error算法应用到非真实感艺术绘制中，他建议每次绘制时随机扰动一定数量的画笔，只有能够减小绘制结果与源图像之间差别的扰动才能被接受。后来，Turk和 Banks[18]把trial-and-error算法应用到向量场流水线型可视化中，建议模糊化向量场的流水线型绘制效果，然后把这一结果与一预先定义的常量比较，从而来评估流水线型可视化的质量。

Trial-and-error算法能够适用于SBR的所有情况，但是需要花费大量的计算时间，而且有时很难找到一个合理的建议机制。实际上，在SBR中用的最普遍的还是贪婪算法。

3.2 基于贪婪算法的SBR

贪婪算法通过精心设计算法步骤，启发式地确定画笔位置，贪婪地放置画笔直到产生用户满意的绘制效果。它不仅要考虑画笔的颜色、大小、形状信息，而且要考虑画笔的走势等。通过画笔形状、大小的不同设计，以及画笔颜色的不同选择可以实现多种绘画风格的模拟绘制。

Haeberli提出了一种简单的半自动绘画算法[16]。用户只需选择具有一定形状的画笔，然后在绘画区域拖动鼠标，系统就会自动在鼠标点击区域进行自动绘制。画笔颜色会从源图像中相应位置吸取，画笔方向与图像梯度方向一致。这个系统中，需要用户交互地选择画笔、确定画笔位置，算法决定画笔颜色、走向等。

Litwinowicz[19]对Haeberli算法进行了加强，实现了自动绘制。Litwinowicz算法对源图像进行预处理获得方向域，把方向域和源图像作为输入数据。算法在一块空白画布上随机产生画笔位置；然后在确定位置处放置画笔，画笔颜色由源图像确定，方向取自方向域。但Litwinowicz算法只能产生固定大小的画笔，使得整个绘制效果比较机械，缺乏灵活性；对不同细节也无法进行不同程度的表达，从而不能很好地满足视觉需求。因此，Hertzmann[20]对Litwinowicz算法进行了拓展，提出了多层绘制的思想。Hertzmann算法把绘制分为多层进行，使用一组具有不同大小的画笔进行分层绘制，各层以Litwinowicz算法为基础用一组固定大小的画笔绘制。对应每一层有一幅参考图，每层只绘制与参考图像不一致的区域。随着绘制层数的提高，画笔大小不断减小，从而不断丰富细节信息。算法通过控制画笔长度、大小等参数可获得不同的绘制风格。

后来基于贪婪算法的画笔绘制基本以Hertzmann的多层绘制思想为基础，或从画笔颜色的产生角度，或从计算画笔大小的角度对其进行改进，以提高算法效率。D Nehab等[21]提出了一种基于多尺度力矩的美术绘制，运用多尺度方案计算画笔大小，采用参数化机制控制画笔位置，以及画笔的分布密度等，从而实现多层绘制。Y Park和K Yoon的算法[22]中，画笔不直接从源图像中获取颜色，而是模拟真实绘画时所用的调色板，选择调色板中与源图像当前位置颜色最接近的作为画笔颜色。通过调制不同的调色板，此算法也能获得各种令人欣喜的绘制效果。

最近Y Semet等[23]提出了一种交互的人造蚂蚁绘制算法。通过设置多群蚂蚁来完成多层绘制任务。蚂蚁感觉局部环境的能力以及记忆能力使得它们能够在环境中适当位置留下印迹（画笔），即在画布上进行绘制。当蚂蚁的行走步数超过预先设定的最大行走步数，或者跳跃次数超过用户设定的最大跳跃次数，绘制任务就算完成。所有蚂蚁在画布上留下的印迹即为绘制结果。通过设定不同的印迹形状、大小、颜色，可以产生不同的艺术效果。这一人造蚂蚁绘制算法初步体现了“多智能体绘制”的思想，但没能给出绘制环境对多智能体的局部激励机制，以及它们在不同的局部激励下如何展现不同的行为模式，所以绘制蚂蚁仍无法很有效地决定绘制区域需要多大程度上的局部化。文献[23]在以往基于画笔绘制算法的基础上，把多智能体技术引入非真实感艺术绘制中，对基于画笔的非真实感智能绘制方法进行了研究，以此拓展了基于画笔绘制的内容。该算法应用多智能体技术的基本原理把绘制过程分解为一个多任务的创作机制，每层绘制看成一个独立的绘制任务，每个绘制任务由一类绘制智能体完成；各类绘制智能体作为独立的行为者，能通过自身的感知能力获取环境局部激励信息，不断与绘制环境进行交互，在不同的局部激励条件下自适应地规划行为，完成各自的绘制任务。这些智能体并行地在绘制环境中搜索各自的特征像素，并在绘制环境中留下特征绘制信息，从而与其它智能体进行交互，互相协作，形成最终的绘制效果。文献[24]又尝试把一种通用的智能技术—蚁群算法（Ant Colony Algorithm, ACA，也称为蚁群系统(Ant Colony System，ACS)）应用到基于画笔的绘制中。通过设置多个蚁群完成多层绘制（图3显示了把一幅芭蕾女孩的照片渲染成类似油画效果的过程），各个蚁群根据环境中信息素信息自适应地调整自己的行为，并在适当位置留下印迹，从而完成各自的绘制任务。利用蚁群算法的正反馈原理，可以加快可绘制区域的搜索过程；同时绘制蚂蚁之间通过不断的信息交流和传递，有利于找到较好的解，不容易陷入局部最优，从而达到全局优化，使得绘制效果比较均匀、自然。

图3 基于蚁群算法的非真实感绘制[24]

4 未来展望

本文回顾了基于图像的非真实感艺术绘制技术，阐述了其中的理论和方法，用模糊数学、统计学和仿生学的相关理论，分别对非真实感艺术绘制中的颜色传输、基于纹理合成的艺术风格传输、基于画笔的绘制等若干问题进行了系统的分析和评论。

非真实感艺术绘制技术开辟了计算机图形学领域有别于真实感绘制方法的新道路。但并不一定是完美的，NPR仍处于一种不断发展，需要不断改进的状态，今后还需在以下方面做更多的工作：

（1）实时的艺术风格传输算法 在基于二维纹理合成的艺术风格传输方面，从最开始的需要消耗几个小时到实时的风格传输，已经取得了较大的进展，而应用到视频处理还需要较长的时间。基于块拼贴的风格传输将有助于在速度上获得较大的提升。

（2）国画的模拟创作 非真实感绘制艺术技术已经能够比较成功地模拟出油画、水彩画、素描等多种绘画风格，开发能够模拟国画的创作软件是一个新的挑战。可以从国画的颜料特性、扩散规律、光照模型出发进行研究。

（3）交互软件的开发 提高非真实感艺术绘制的框架性能，提高交互操作能力，发展具有一定应用价值的专业软件。

（4）客观的评价标准 非真实感绘制技术着重人们的主观感受，不像真实感绘制已经具有成熟的评判标准，非真实感绘制作为一门新兴的技术仍没有一个科学的评判标准。目前仅能从绘制效率角度进行评价，如何开发出客观的数学模型进行评价有待研究。

[1][加]Thomas Strothotte, Stefan Schlechtweg著. 非真实感图形学-造型、绘制与动画技术[M]. 叶修梓,万华根, 张 引译. 北京: 电子工业出版社, 2004.10-17.

[2]钱小燕, 肖 亮, 吴慧中. 自适应画笔分布的非真实感绘制[J]. 工程图学学报, 2006, 27(2): 58-63.

[3]钱小燕, 肖 亮, 吴慧中. 一种流体艺术风格的自适应 LIC 绘制方法[J]. 计算机研究与发展,44(9): 1588-1594.

[4]Ruderman D L, Cronin T W, Chiao C C. Statistics of cone responses natural images: Implications for visual coding [J]. Journal of Optical Society of America,1998, 15 (8): 2036-2045.

[5]Reinhard Erik, Ashikhmin Michael, Gooch Bruce, et al.Color transfer between images [J]. IEEE Computer Graphics and Applications, 2001, 21(5): 34-41.

[6]赵国英, 向世明, 李 华. 高阶矩在颜色传输中的应用[J]. 计算机辅助设计和图形学学报, 2004, 16(1):62-66.

[7]钱小燕, 肖 亮, 吴慧中. 模糊颜色聚类在颜色传输中的应用[J]. 计算机辅助设计与图形学学报,2006, 18(9): 1332-1336.

[8]Hertzmann A, Jacobs, E C, Oliver N, et al. Image analogies [C]//Proceedings of SIGGRAPH2001, 2001:327-340.

[9]徐文华, 魏宝钢, 潘云鹤. 基于纹理合成的图像艺术风格学习[J]. 武汉大学学报, 2003, 26(3):115-119.

[10]Ashikhmin M. Synthesizing natural textures [C]//Proceedings of 2001 ACM Symposium on Inter-Active 3D Graphics, 2001: 217-226.

[11]钱小燕, 肖 亮, 吴慧中. 快速风格迁移[J]. 计算机工程, 2006, 32(21): 15-17, 46.

[12]Hertzmann A. Survey of stroke-based rendering [J].IEEE Computer Graphics and Applications, 2003,3(4): 70-81.

[13]Secord A. Weighted voronoi stippling [C]//Proc.2ndAnn.Symp. Non-photorealistic Animation and Rendering (NPAR2002), ACM Press, 2002: 27-43.

[14]Deussen O, et al. Floating points: a method for computering stipple drawing [J]. Computer Graphics Forum, 2000, 19(3): 27-43.

[15]Hoff III K, Culver T, Keyser J, et al. Fast computation of generalized voronoi diagrams using graphics hardware [C]//Proceedings of SIGGRAPH99,Computer Graphics Proceedings, Annual Conference Series, 1999: 277-286.

[16]Hausner A. Simulating decorative mosaic [C]//Proc.Siggraph 2001, 2001: 573-578.

[17]Haeberli P E. Paint by numbers: abstract image representations [J]. Computer Graphics, 1990, 24(4):207-214.

[18]Turk G, Banks D. Image-guided streamline placement [C]//SIGGRAPH 96 Conference Proceedings, 1996: 453-460.

[19]Litwinowicz P. Processing images and video for an impressionist effect [C]//Proc. Siggraph 97, ACM Press, 1997: 407-414.

[20]Hertzmann A. Painterly rendering with curved brush strokes of multiple sizes [C]//Proc. SIGGRAPH’98,1998: 453-460.

[21]Nehab D, Velho L. Multiscale moment-based painterly rendering [C]//Proceedings of the Brazilian Symposium on Computer Graphics and Image Processing, 2002: 244-251.

[22]Park Y, Yoon K. Adaptive brush stroke generation for painterly rendering [C]//Proceedings of Eurographics 2004, Short Presentations, 2004: 65-68.

[23]Semet Y, O’Reilly U M, et al.An interactive artificial ant approach to non-photorealistic rendering [C]//The Genetic and Evolutionary Computation Conference(GECCO’04), 2004: 26-30.

[24]钱小燕, 肖 亮, 吴慧中. 一种非真实感绘制的多智能体仿真方法[J]. 系统仿真学报, 2006, 18(10):2836-2839.

[25]钱小燕, 肖 亮, 吴慧中. 一种基于分布均匀度的非真实感蚁群绘制方法[J]. 中国图像图形学报,2006, 11(12): 1792-1798.