南丰蜜桔造型

林江鹏+陆玲

摘要：根据南丰蜜桔近似球形的特征，通过对球面进行变形模拟蜜桔形状。首先设计变形函数将球面变形得到南丰蜜桔叶整体形状；再设计纹理的变形函数将光滑表面变凹凸的效果；最后进行真实感绘制完成南丰蜜桔的造型。通过与真实图片的结果对比，表明其真实感造型效果较好。

关键词： 南丰蜜桔；变形；真实感

中图分类号：TP391.9 文献标志码：A 文章编号：1009-3044（2015）30-0142-02

Realistic Modeling for Nanfeng Orange

LIN Jiang-peng， LU Ling

（School of Information Engineering， East China Institute of Technology， Nanchang 330013，China）

Abstract： According to the characteristics of the Nanfeng orange that look like sphere shape ， we deform the sphere to form the shape of the Nanfeng orange. First， we design deformation function to deform the sphere and form whole shape of the Nanfeng orange. Second，the grain deformation function is designed and concave-convex grain is formed . Finally， the deformation sphere is rendered and the Nanfeng orange is modeled . By comparison with the results of real images， it shows that the effect of real sense is better.

Key words： nanfeng orange； deformation； realistic

1 绪论

南丰蜜桔主要产于江西省南丰县，是我国名优果树品种之一，历史上曾被列为朝贡珍品，被誉为“桔中之王”。南丰蜜桔的真实感造型，对于虚拟植物的研究有一定现实 意义。

一些研究者采用各种方法对植物果实进行了真实感模拟，雷蕾等[1]采用Bezier曲线拟合黄瓜果实轴线方程， 并设计其截面半径的各分段函数， 用随机函数控制果实表面的凸凹。王景波等[2] 以一种典型的几何纹理算法对不同果实进行3D 造型，针对果实生长不同阶段的特性建立数学模型，实现了静态造型和动态仿真。刘骥等[3]通过果实主轴线和截面曲线参数方程计算果实表面的网格面，在曲线方程上叠加扰动函数解决了果实生长过程中的形变问题。刘格林等[4] 建立了良种南瓜的生长时期三个阶段的可视化数学模型， 并模拟这三个阶段的生长过程。金席卷等[5]以柑橘为例，采用Bezier 曲线拟合柑橘果实的外轮廓，利用MapL 系统来对柑橘表面凹凸的局部特征性进行模拟。王立臣等[6]根据主轴控制点和横截面半径控制函数模拟杨桃果实的几何造型， 并用横截面半径上的随机函数来控制果实表面的凸凹纹理。陆玲等[7] 使用凹凸纹理处理方式对椭球面参数方程进行变形，模拟芒果、水蜜桃、香蕉等不同形状植物果实。

综上所述，较小有对蜜桔进行真实感模拟，本文采用文献[7]的方法，对南丰蜜桔进行可视化造型。

2 南丰蜜桔的几何形状造型

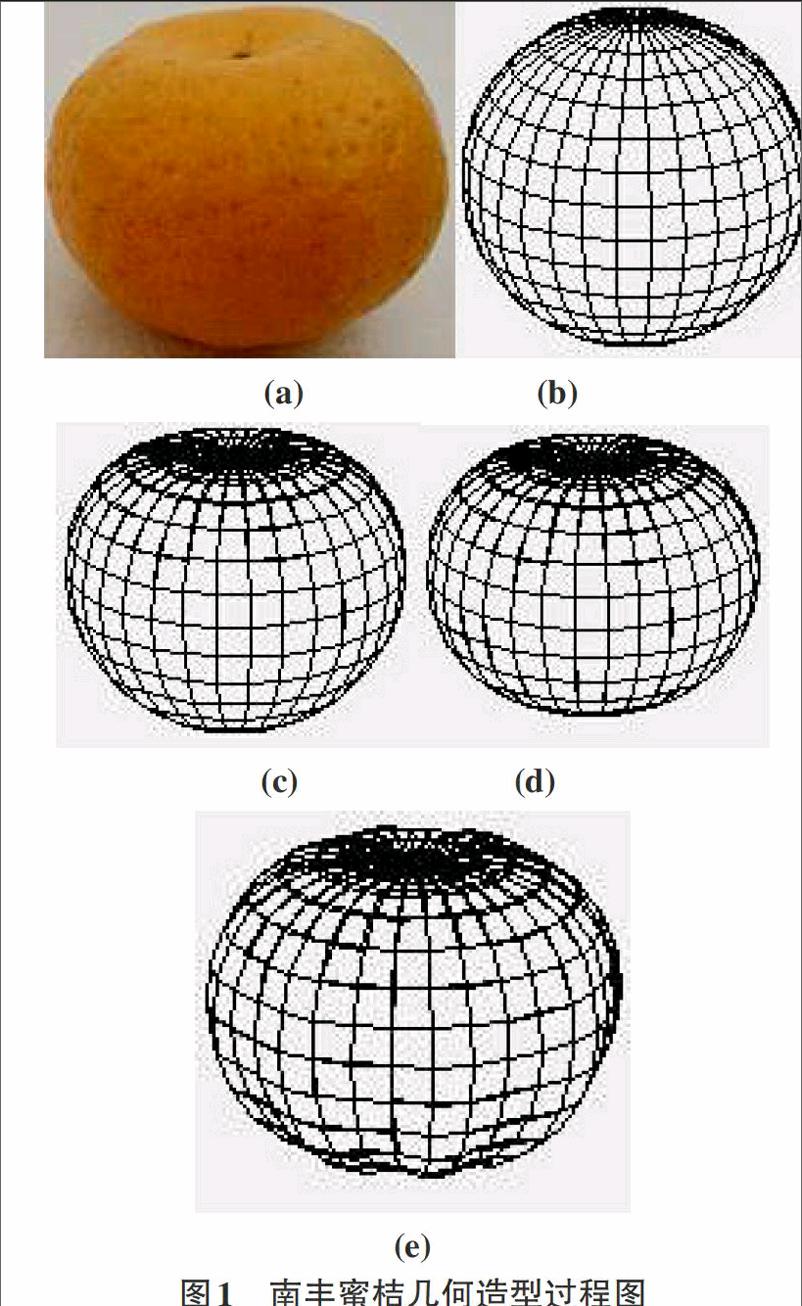
用球面参数方程定义蜜桔的初始形状，根据图1a的南丰蜜桔的大体形状，设计球面参数方程如下（如图1b）：

x（u，v） =rcos（u）cos（v）

y（u，v）=rcos（u）sin（v） （1）

z（u，v） =rsin（u）

（-/2u/2，0v2）

式中：r为球半径，这里r=60，单位为像素（下同）。

对球面沿法向量变形后的参数方程为：

x（u，v） =rcos（u）cos（v）+ag（u，v）

y（u，v） =rcos（u）sin（v）+bg（u，v） （2）

z（u，v） =rsin（u）+cg（u，v）

（-/2u/2，0v2）

式中（a，b，c）为点（x，y，z）处的单位外法向量，g（u，v）就是本文重点设计的变形函数，它是由多个函数组成：

g（u，v）= g1（u）+ g2（u）+ g3（u，v）+ g4（u，v）

1）上下两端模拟

根据南丰蜜桔的形状特点，上下两端向内凹进，采用高斯函数模拟凹进效果。

上端凹进（如图1c）：

g1（u）=-A1exp（-（u+/2）2/s2）

式中：A=r/3， s= r/100。

下端凹进（如图1d）：

g2（u）=-Aexp（-（u-/2）2/s2）

式中：A2=r/3， s= r/100。

2）周期凹凸模拟

由于桔瓣的影响，蜜桔外型具有小幅度的周期凹凸，采用正弦函数进行变形：

g3（u，v）=A3sin（8v）

但根据图1a中上端平坦下端凹凸明显特征，将u参数与A3相关：

g3（u，v）=A3 （u+/2）/ sin（8v）

式中A3=1，如图图1e所示。

（a） （b）

（c） （d）

（e）

3 南丰蜜桔的颜色及纹理造型

根据南丰蜜桔的颜色，在HIS颜色模型中，设定色度为30度，饱和度为0.8，亮度计算采用简单光照模型中的漫反射与环境光[8]， 如图2a所示，从图中看出模拟效果表面太光滑，应加入表面凹凸纹理，凹凸纹理函数设计为：

g4（u，v）= ∑Bi （u+/2） （u-/2）|sin（fiu +Ci sin（kiv+cos（diu））| 上 式中的 （u+/2） （u-/2）主要用于控制上下两端无明显凹凸纹理。

图2b中的各项参数值如下：

B0=0.1， f0=28， C0=0.5， k0=32， d0=25

B1=0.1， f0=10， C0=0.3， k0=25， d0=20

B2=0.1， f0=10， C0=0.3， k0=27， d0=30

以上参数可以适当修改。

从图1a中可以看到蜜桔顶部有一个小暗圈，因此当u在-89度和-86度范围时，将颜色的饱和度S变为0.3，如图2c所示。

对于蜜桔的低部形状如图2d所示的图像，旋转图2c的蜜桔得图2e效果图，当u在80度和85度范围时，将颜色的色度改为100度、饱和度S变为0.3模拟与茎接处的绿色环形部分，如图2f所示。由于变形函数g3（u，v）的影响，使绿色环形也变形，为了避免这种情况，当u> 80度时，变形函数中去除g3（u，v）的影响，如图2g所示，加上绿色环形如图2h所示。

（a） （b）

（c） （d）

（e） （f）

（g） （h）

4 南丰蜜桔真实感绘制

南丰蜜桔造型伪程序如下：

for（u =-90；u<=90；u=u+du）

for（v = 0；v<=360 ；v=v+dv）

{ 利用式（1）计算小面块的顶点坐标

计算小平面单位外法向量（a，b，c）

if（u<80）

利用式（2）沿外法向量方向对球体进行变形

小面块绕x轴旋转

再次计算小平面外单位法向量（a，b，c）

用简单光照模型计算小面块的亮度I

if（u>=-89&&u<=-86）

将H=30、S=0.3、I转换为R、G、B

else if（u>=80&&u<=85）

将H=100、S=0.3、I转换为R、G、B

else

将H=30、S=0.8、I转换为R、G、B

利用深度缓存算法对小面块进行消隐处理

对于面块中可见的像素用RGB显示出来

}

5 结束语

本文对南丰蜜桔的造型有完整的数学模型，计算方法简单，造型速度快，参数易于调控，灵活性比较好，该方法对于后续南丰蜜桔生长建模有一定的实用价值。

参考文献：

[1] 雷蕾，郭新宇，周淑秋，等.黄瓜果实的几何造型及可视化研究[J].计算机应用与软件，2006，23（5）：24-25.

[2] 王景波，陆玲.基于Opengl 的3D 果实造型研究[J].计算机工程，2010，36（4）：279-280.

[3] 刘骥，曾令秋，朱庆生.基于曲线参数方程的植物果实造型[J].计算机应用研究，2009，25（11）：3474-3476.

[4] 刘格林，陆玲，阎旭红.南瓜果实生长的几何造型[J].计算机应用与软件，2008，25（3）：171-172.

[5] 金席卷，敬松，方逵.虚拟植物果实的可视化建模技术研究[J].农机化研究，2012（10）：176-179.

[6] 王立臣，淮永建，杨刚，等.杨桃果实几何造型及可视化研究[J]. 农机化研究，2009（7）：86-89.

[7] 陆玲，周书民.植物果实的几何造型及可视化研究[J].系统仿真学报，2007（19）.

[8] 陆玲，桂颖，李丽华.计算机图形学[M].北京： 电子工业出版社，2012.