一个带间隙连接结构对梁基频漂移影响研究
卫洪涛,孔宪仁
(哈尔滨工业大学 卫星技术研究所,哈尔滨 150001)
0 引言
随着航天技术的进步,航天器构造趋向于复杂化,其结构的非线性振动是航天工程领域一直都非常感兴趣的课题,尤其是航天器地面振动试验中的频率漂移现象得到了研究人员的重点关注。航天器的基频在星箭力学环境中是最重要的参数之一,因此研究航天器频率漂移的机理对于航天工程具有重要意义,不但能够为航天器的设计和制造提供重要参考价值,而且可以为抑制已经做好的航天器的频率漂移提供解决思路。一般认为,航天器的组成材料,如蜂窝夹层板以及某些组合的连接结构存在非线性因素,是整个航天器频率漂移的主要原因。
本文研究了一个一端夹支、另一端带非线性连接结构的梁的非线性振动,主要目的是研究连接结构的非线性对整梁振动的幅频响应的影响。非线性边界条件下梁振动研究,前人的文献中已经有很多涉及了,如A. Ferri等在一系列的文章中[1-5]研究了梁的两端在不同边界支撑条件下的振动情况:文献[1]提出了一个航天器上的套筒连接结构的力学模型,该模型考虑了连接结构的间隙、阻尼及干摩擦力;文献[2]利用简化的套筒连接结构研究了柔性梁系统的振动,利用单振型近似及数值方法得到了系统的幅频响应;文献[3]研究了阻尼和摩擦边界条件对梁的振动的影响,分别对3种不同的摩擦力情况进行了讨论;文献[4]研究的连接结构模型考虑了面内的弹簧力、梁与套筒内壁摩擦导致的面内摩擦力、套筒连接引入系统的横向剪切弹力及端点弯矩,利用线性振型,用伽辽金近似法研究了一端夹支、另一端具有套筒连接边界条件的梁的振动,着重讨论了系统的阻尼与连接结构模型参数之间的关系;文献[5]考虑了一个具有特殊边界条件的梁的振动,利用谐波平衡法和多振型近似数值积分法,研究了系统响应和边界条件参数之间的关系,对比了单振型和多振型研究对结果的影响。A. Ferri等的工作在研究间隙的存在对系统响应的影响方面涉及比较少。S. M. Wiedemann研究了几种非线性边界条件下梁的振型,并且提出了一种求任意边界条件梁的振型的方法[6]。在研究梁振动系统中间隙对系统振动的影响方面,有如下代表:F. C. Moon等研究了一端夹支、另一端具有阻挡的悬臂梁的受迫振动,采取了类似振型转换的方法即单振型近似法和伽辽金方法,利用一个特殊点的振幅连续简化了系统的振动方程(这里称其为连续振型法以区别于振型转换法),揭示了系统在此研究下的混沌振动[7];H. Chuang研究了一端夹支、另一端具有带间隙的单线性弹簧阻挡的非线性振动,总结了在其以前的文献研究中的两种方法即力积分法和振型转化法,并分别利用这两种方法对其模型进行了数值研究,讨论了阻挡弹簧的刚度与间隙大小对系统响应的影响[8]。
本文的研究主要基于A. Ferri的简化套筒连接模型,仅考虑端点的横向剪切弹力,给连接结构引入了间隙,利用改进的振型转化法以及连续振型方法,即采用伽辽金法推导了此条件下梁的运动方程,并且针对一个算例,讨论了连接结构的间隙对梁的幅频响应的影响。
1 系统建模
本文用以研究间隙对梁的非线性振动影响的系统模型如图1所示。

图1 梁系统结构图Fig. 1 Schematic diagram of the beam system structure
在图1中:F为均布载荷激励力;P(t)为端点所加的预紧力;Δ为所加间隙;K为横向剪切反力刚度。与文献[8]不同的是,这里的端点边界条件为上下均有弹簧提供端点反力。
1.1 梁的运动方程
图1所示边界条件的梁系统,根据端点位移的大小其运动方程有两种:悬臂梁运动方程和受连接结构限制的梁运动方程。当端点在间隙内运动时,系统可以认为是悬臂梁;当端点接触到连接结构的内壁时,是具有非线性连接结构的梁系统。
首先考虑梁连接结构处无预紧力P( t)作用时的情况,带预紧力的情况在下文中阐述。系统的运动方程可以表达为:
1)悬臂梁
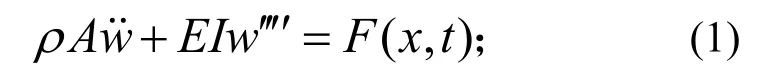
2)非线性连接结构梁[4]
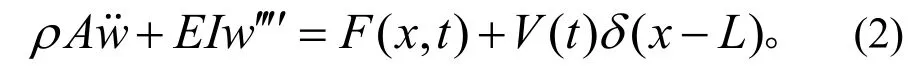
在(2)式中:V(t)为端点弹簧提供的横向反力;δ( x - L)为狄拉克函数;在下文的数值求解时,令激励力F( x,t)沿x方向无变化即 F( x,t) = Fc os(Ω t),其中F为幅值;ρA为单位长度质量;A为梁横截面积;I为惯量;E为弹性模量。利用伽辽金法求上述方程的近似解,不失一般性,假设时间t1之前梁的端点在间隙内运动,也就是系统运动在悬臂梁状态,则梁上任一点的横向位移可以表示为

式中ϕn(x)为悬臂梁振型,an( t)为各阶振型的振幅,此时,端点位移 -Δ <w( L, t)<Δ。假设t1至t2时间段为梁的端点与连接结构的内壁接触时间段,也就是系统运动处在受限运动状态,那么此段时间内,梁上任一点横向位移可以表示为
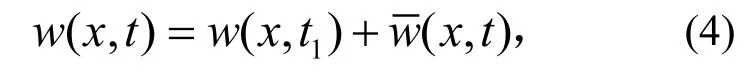
其中
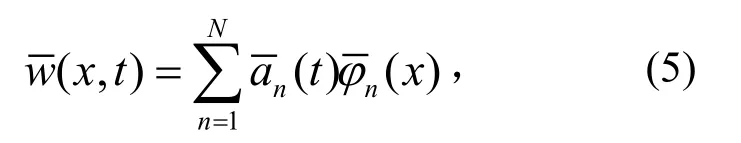
1)悬臂梁

2)非线性连接结构梁
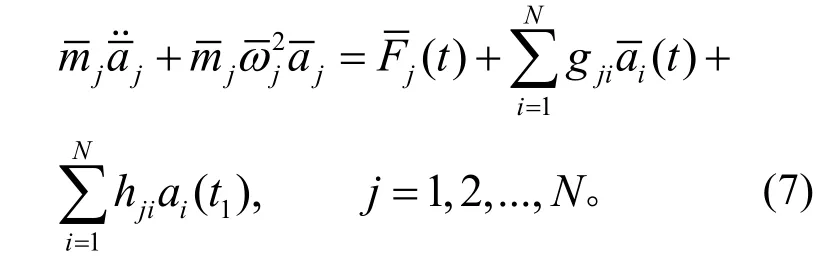
在(6)、(7)式中:

对于一个实际的算例,引入系统参数后对上面的微分方程组进行数值求解,当系统振动在悬臂梁和受限振动状态之间转换时,需要知道转换后方程的初值,即t1+、t2+时刻的位移和速度(作者按:t1、t2时刻为满足切换条件的时刻,是整个时间区间上的一点;而 t1+、t2+是表示过了切换时刻的时刻,如果用时间区间表示:(0,t1-) t1(t1+,∞)),利用振型的正交性由(4)式得到

将(3)、(5)式代入(8)式中,利用振型的正交性可以得到在t1+时刻受限运动状态各振型方程的初值:
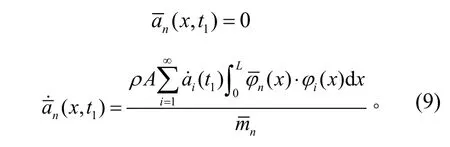
当时刻t2梁的端点从受限状态回到悬臂梁状态时,有


考虑在系统端点处施加预紧力时,仅需在 (1)、(2)式右端加入常量力P,后续处理步骤不变,且转换状态时系统初值也不受影响。即:
1)悬臂梁(带预紧力)

2)非线性连接结构梁(带预紧力)

后续处理方法如(3)式至(13)式。
1.2 受限振动梁振型
在套筒连接结构内有间隙的情况下(见图1),假设套筒对梁施加横向剪切反力等同于理想弹簧,不考虑冲击效应,当梁端点接触到连接结构内壁后,系统运动立刻在受限状态下振动,此时梁等同于端点处有连接结构的边界条件,受到套筒的横向剪切力。根据S. M. Wiedemann的方法[6]求此边界条件梁的振型,有边界条件:
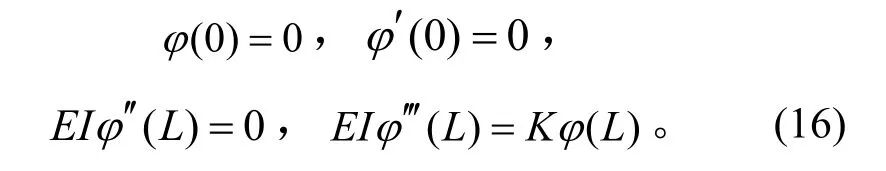
假设 ϕn(x)为所要求的振型表达式,并将上面4个边界条件引入到梁振型的一般形式,则
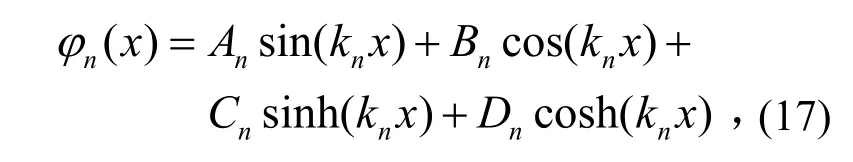
其中 kn、An~Dn为各振型参数。由(16)式的前两个边界条件可以得到 Ci=-Ai,Di=-Bi,将其代入到(16)式后面的边界条件中,可以得到矩阵的表达形式

其中 dij为引入边界条件后的表达式,这里用符号代替。简单令 Ai= 1,由(18)式可以得到振型函数系数Bi的表达式,至此An、 Bn、 Cn、 Dn均已解出,然后利用式(18)An、 Bn具有非平凡解的条件,矩阵的行列式为零,可解出各阶振型表达式对应的kn。
对于实际的系统,可以求得不同弹簧刚度时受限振动梁的振型,如图2所示。

图2 不同的边界弹簧刚度时梁的一阶振型Fig. 2 First order modes for different boundary spring’s stiffness
由图2可以看出,随着端点弹簧刚度由0递增,从振型上看,梁的端点位移实际上是先增大到一定程度而后开始逐渐减小。
2 算例及讨论
针对一个实际的例子来求数值解。在前人的研究中,为了计算的方便,往往在一定的假设条件下对梁位移进行单振型简化。假定振型之间具有正交性,各振型之间没有内共振;在这样的前提下[9],单振型近似的结果也是有意义的。本文首先利用单振型近似法进行研究,研究中还利用改进的状态转换法和连续振型法[7]两种不同的处理方法进行求解,并对比了它们的结果。系统参数如下:
单位长度质量ρA=3.255 2 kg/m;
梁长L=2 m;
梁横截面积A=1.470 3×10-4m2;
惯量I=1.014×10-8kg/ m2;
弹性模量E=7.45×1010N/ m2;
端点弹簧刚度K=4.7×102N/ m。
2.1 单振型近似法
如上所述,悬臂梁振型和非线性连接结构振型均取1阶。在这种条件下,伽辽金法处理后的系统运动方程有(带预紧力情况略)

1)悬臂梁

2)非线性连接梁
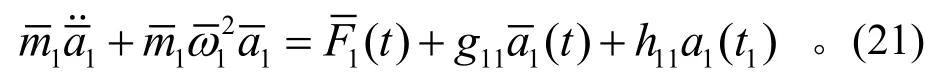
在(20)、(21)两式中,下标代表一阶。

对系统进行扫频激励,其步骤如下:
1)首先确定扫频区间[Ω1, Ω2]、幅值F,将F cos(Ω t ),Ω1<Ω<Ω2代入方程,利用 MATLAB,Ode4求解系统,积分步长为10-4s;
2)数值求解时,始终检查梁端点的位移大小,当端点位移的绝对值时,系统振动的状态发生改变,用MATLAB内建的Stateflow进行逻辑控制,将方程各变量系数及积分初值转换,可以得到该激励频率Ω下,梁端点位移的时域响应;
3)取20 s的时间历程,舍弃前面8 s的数据,以保证不受瞬态响应的影响,取保留数据的最大值与最小值之差的一半为响应幅值;
图3和图4分别表示利用振型转换法得到的在有、无预紧力条件下的幅频响应图。

图3 无预紧力梁端点幅频响应(振型转换法)Fig. 3 Frequency response of the beam end without preload (mode transfer method)

图4 有预紧力梁端点幅频响应(振型转换法)Fig. 4 Frequency response of the beam end with preload (mode transfer method)
2.2 带阻挡的悬臂梁
文献[7]在研究带阻挡的悬臂梁的振动时,利用了同上面单振型的振型转换方法类似的方法,巧妙地利用梁上特定长度点的振幅对系统的振幅进行连续性处理,从而不必求系统切换时微分方程的初值,这里采用其思想研究单振型时系统的幅频响应情况,以此与上面的振型转换方法进行互相印证。主要方法是,梁任一点的横向位移可以表达为:

其中: asϕ1(L)=Δ。考虑梁上一个特殊点x1,该点可令ϕ1(x1)=1,那么在该点,梁的横向位移可以表达为:

令 w( x1, t) <as时,该点振幅 a1( t) =a( t),w( x1, t) >as时,该点振幅 as+a2( t) ϕ2(x1) =a( t )。可以得到:

利用(24)式,可以将振型转换法的系统方程统一为a( t)变量,从而不必在系统切换时求a1( t)和a2( t)的初值。
利用上面的处理步骤,数值求解步骤与上面相同,可以求得系统的幅频响应。图5和图6分别表示利用连续振型法得到的在有、无预紧力条件下的幅频响应图。
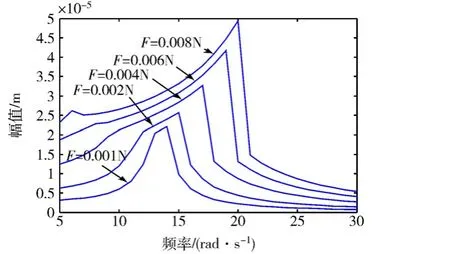
图5 有无预紧力梁端点幅频响应(连续振型法)Fig. 5 Frequency response of the beam end with and without preload (continuous mode method)

图6 有预紧力单振型梁端点幅频响应(连续振型法)Fig. 6 Frequency response for one mode approximation with preload (continuous mode method)
从上面的结果看,两种方法得到在不同量级激励力作用下和在有、无预紧力前置两种条件下的系统幅频响应图几乎完全相同。单振型方法仅仅是对实际模型的一种近似,但其结果对于研究间隙对一端夹支、另一端带连接结构的梁振动的影响是有参考意义的。可以看出,当系统没有预紧力时,间隙的存在令梁系统具有“硬弹簧”属性,当激励力增加,端点的振幅响应峰值持续向高频漂移。当系统存在预紧力时,其幅频响应图与无预紧力时的结果对比相差很大:小激励力时系统的基频高于无预紧力时的情况,端点的幅频响应首先呈现“软弹簧”特性,随着激励力增大,响应峰值向低频漂移;当向低频漂移一定程度后,继续增大激励力,系统响应反而呈现“硬弹簧”特性,响应峰值向高频漂移。
3 结论
本文针对一个一端夹支,另一端有带间隙的连接结构的梁系统模型,将系统简化后研究了连接结构中的间隙对系统振动幅频响应的影响。简化后的模型仅仅考虑了连接结构对梁的横向剪切力。采用了改进的振型转换法以及连续振型法两种方法,并按伽辽金法处理从而得到数值求解方程,研究了单振型近似情况下梁在递增激励力作用下的频率漂移。从结果来看,间隙的存在结合有、无预紧力的前提条件,可以令系统的幅频响应呈现软弹簧或者硬弹簧的属性,本文的结果对于研究航天器地面振动试验中的频率漂移现象具有参考价值。
(
)
[1] Ferri A A. Modeling and analysis of nonlinear sleeve joints of large space structures[J]. Journal of Spacecraft and Rockets, 1988, 25(5): 354-360
[2] Bindemann A C, Ferri A A. Large-amplitude vibration of jointed flexible structures[C]//32ndAIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics, and Materials Conference, Baltimore, MD, United States, 1991: 2737-2744
[3] Ferri A A, Bindemann A C. Damping and vibration of beams with various types of frictional support conditions[J]. J Vib Acoust, 1992, 114(3): 289-297
[4] Bindemann A C, Ferri A A. Large amplitude vibration of a beam restrained by a non-linear sleeve joint[J]. Journal of Sound and Vibration, 1994, 184(1): 19-34
[5] Whitemana W E, Ferri A A. Multi-mode analysis of beam-like structural subjected to displacement-dependent dry friction damping[J]. Journal of Sound and Vibration, 1997, 207(3): 403-418
[6] Wiedemann S M. Natural frequencies and mode shapes of arbitrary beam structures with arbitrary boundary conditions[J]. Journal of Sound and Vibration, 2007, 300(1-2): 280-291
[7] Moon F C, Shaw S W. Chaotic vibrations of a beam with non-linear boundary conditions[J]. International Journal of Non-Linear Mechanics, 1983, 18(6): 465-477
[8] Tsai Hsiang-Chuan, Wu Ming-Kuen. Methods to compute dynamic response of a cantilever with a stop to limit motion[J]. Computers and Structures, 1996, 58(5): 859-867
[9] Nayfeh A H. A parametric identification technique for single-degree-of-freedom weakly nonlinear systems with cubic nonlinearities[J]. Journal of Vibration and Control, 2003, 19(3-4): 317-336

