多轴随机振动环境的疲劳损伤机理浅析
周兴广
(北京强度环境研究所,北京 100076)
0 前言
在振动环境模拟试验领域,多轴振动试验在产品故障模式复现和模拟精度方面具有显著的优势,它能够真实地模拟实际的动力学环境,暴露产品在单轴激励振动方式下不易被发现的缺陷和隐患。一些已按规范通过单轴振动的产品,在多轴振动中会暴露出新的故障,而这些故障模式在实际使用过程中也会出现,从而表明多轴振动环境试验可以更逼真地模拟使用环境[1-2]。
随机振动试验是考核产品结构动强度及环境适应性的重要手段,是暴露结构缺陷和鉴定设备承受使用环境能力的一种有效方法。通过对试验现场振动测试数据的分析,发现产品在使用过程中的振动环境绝大多数为多轴随机环境,因此随机载荷作用下结构和部件的动强度分析和疲劳寿命的预测尤为重要。据统计,工程构件多是因承受随机载荷作用而失效,疲劳损伤破坏约占到 80%以上。所谓疲劳损伤,是指产品及构件在应力或应变的反复作用下所发生的性能变化。随机载荷下疲劳损伤和可靠性的评价是一个关键的问题[3]。
1 多轴随机振动环境下的循环计数方法
多轴随机振动指的是同时使用多个振动台激励一个试验件的高斯分布宽带随机振动。文中主要针对高斯宽带随机振动激励的损伤机理进行初步探讨,分析多轴振动损伤机理的计算方法及振动特征与激发产品缺陷、加速产品失效的关系。
多轴振动台可分为两类:一类是单方向激励,即多个振动台平行激励试件,当各个振动台激励相位相同时形成多台同步振动(图1);另一类是3个方向激励,即振动方向相互垂直,形成三轴相互垂直振动(图2),或者形成三轴向六自由度的空间运动(图3)。试验数据表明:在多轴随机振动环境下,试件的应力响应与其受到的速度功率谱是等比例关系,速度功率谱可以通过试件上固定的加速度传感器测得的时域信号转化为加速度功率谱而计算得出。

图 1 单方向多台激振系统Fig. 1 One-way and multi-platform vibration system

图 2 三轴振动系统Fig. 2 Triaxial vibration system

图 3 三轴向六自由度振动系统Fig. 3 6-DoF triaxial vibration system
在随机载荷作用下疲劳损伤机理的研究中,累积疲劳损伤分析方法在各种试件的载荷分析中都起着重要的作用。最早由Matsuishi和Endo[4]提出的主要以雨流计数法(Rainflow Counting)为核心的时域疲劳寿命估计方法应用较为广泛,并已成为标准的循环计数方法。雨流计数法对产品所承受的载荷时间历程进行循环计数,根据累积疲劳损伤理论计算出试件的疲劳循环寿命。经典的雨流计数能够处理单轴载荷的历程,对多轴载荷的处理仅限于比例载荷。此后,Wang和Brown提出多轴疲劳计数法作为新的损伤计算方法,该方法采用传统的相对当量应变法,其中循环被定义为从零到最大值的增加[5]。
Brown等指出了传统的雨流计数方法的局限性,提出多轴非比例雨流计数方法和疲劳损伤计算流程[6]。Socie对多轴非比例随机载荷中的4个问题,即循环应力应变模型、循环计数方法、损伤模型和损伤累积模型进行了分析。指出Bannantine-Socie方法及Wang-Brown方法可应用于比例载荷,但用于定义具有平均应力的循环中仍有困难。
Anthes对经典的雨流计数方法进行了修正,对于应力-应变路径的不封闭部分采用了虚拟滞环的概念,能够考虑载荷顺序的影响。Langlais等[7]通过对单轴循环计数方法简单修正后提出了多轴循环计数方法。在单轴情况下,应力和应变是同相的,应变中的一个往复与应力中的一个往复相一致。而多轴情况下应力和应变过程并不同相,如果仍对数据进行计数,将难以保证不同的数据组间的关系。为了保证重要信息不被略去,必须考虑其他辅助通道的数据关系,从而实现多轴循环的计数。
Dirlik等提出了一个宽带随机应力作用下疲劳寿命估计的经验闭合解,即Dirlik经验公式,以计算平稳高斯应力造成的疲劳损伤[8]。公式针对平稳的、各态历经的高斯过程,从功率谱密度估计雨流计数法,利用波峰和波谷的近似模型,给出了一种多轴随机振动环境下的循环计数方法,该方法成为目前应用最广泛的随机应力疲劳寿命估计方法。
2 多轴振动疲劳损伤分析方法
多轴疲劳是指疲劳损伤发生在多轴循环加载条件下,至少有两个方向施加的应力独立随时间变化。其变化可以是同相位、比例的,也可以是非同相位、非比例的。
多轴随机载荷下的损伤累积研究并不多见。Fash等[9]针对多轴变幅载荷下的构件进行了分析,通过计算得到确切的峰值和谷值,采用传统的局部应变寿命的概念进行疲劳寿命预测。
相对于单轴疲劳而言,多轴疲劳无论在力学、试验研究乃至物理机制方面都更为复杂。因为随着3个主应力相对比值的改变,损伤可以在不同方向、不同平面内形成。此外,在多轴情况下的循环应力应变特性,损伤的取向、形状、扩展方向、速率以及疲劳寿命等均受到更多因素的影响。由于多轴疲劳损伤机理和失效过程的理论分析与试验研究都还不足,尚有许多基本问题没有解决,所以还没有形成统一的理论[10]。
现有的多轴疲劳损伤分析方法主要有以下3种[11]。
1)等效应力-应变法:基于一定的静强度理论,利用Von Mises最小畸变能原则或Tresca屈服准则等,对多轴应力状态下的应力(应变)进行等效。将等效应力(应变)作为损伤参量,估算出多轴状态下构件的寿命。等效应力-应变法不涉及到具体的多轴疲劳破坏机理。
2)能量法:基于能量建立疲劳损伤度,主要考虑多轴和平均应力对材料变形的影响。能量法认为塑性功的累积是产生材料不可逆损伤进而导致疲劳破坏的主要原因,而材料达到疲劳断裂时所需要的能量与加载方式无关。能量法可以应用于多轴载荷条件下比例及非比例加载的寿命估算,但是能量法本身是标量,不能反映出多轴疲劳破坏面,在估算长寿命时误差较大。
3)临界损伤平面法:它不仅考虑应力、应变的大小,而且还考虑到它们所在的平面及方向,以建立一种与最大损伤平面上的应变参数有关的疲劳
损伤参量。利用临界平面理论,可以对比例及非比例两种加载情形进行寿命估算研究。该法反映了多轴疲劳变化破坏面具有一定的物理意义。但目前各种临界损伤平面法基本上是基于试验的经验公式,应用范围窄,且包含一些物理意义不明确的常数。
等效应力-应变法虽然不能反映材料内部机理,但是它有效利用了单轴疲劳中成熟的理论和经验数据,使用和计算方便,同时也能够给出疲劳损伤的一个初步估计,所以实际工程中仍在广泛应用。目前,多轴疲劳频域分析方法就是以等效应力-应变法为基础,在频域内利用随机应力的统计参数来分析疲劳损伤的。
3 多轴正态随机振动的疲劳损伤计算
正态随机是目前较为广泛使用且很重要的应力分布方式,很多统计方法都是由此分布引出的。多种类型的产品在涉及疲劳损伤问题时都可应用正态随机分布。
疲劳损伤分析方法的基本思路是从随机应力的统计特性功率谱估计出峰值应力在单位时间内的期望循环次数的概率密度函数,根据Miner准则计算出期望疲劳损伤,最后得到疲劳损伤和疲劳寿命的估计。
正态分布的概率密度函数可表示为

其中:-∞<t<+∞;-∞<μ<+∞;σ>0 ;
正态分布的累积分布函数可表示为
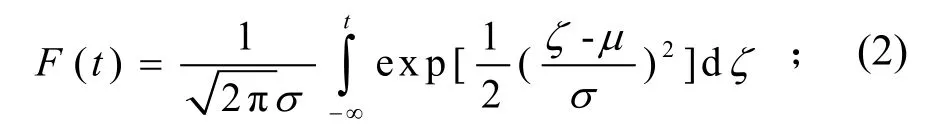
此分布关于其均值μ对称,标准差σ表示离散度。对变量进行简单变换,则(2)式得累积分布函数变为

由应力y1与它的一阶导数 y2和二阶导数y3的联合峰值概率密度函数 f (y1y2y3)计算出单位时间内应力峰值的期望循环次数:

根据 E [n(y1)] 估计其概率密度函数为
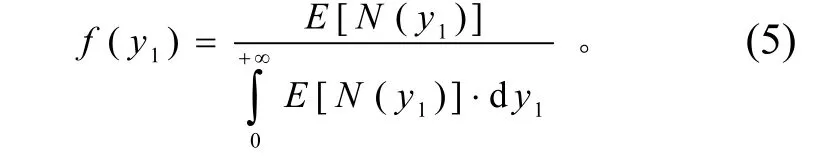
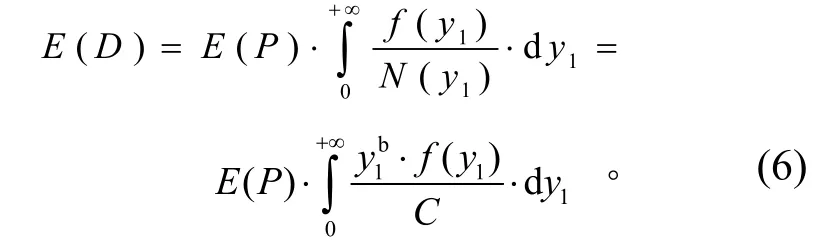
应力在作用时间 T 后引起的期望疲劳损伤

当 E [D(T)] = 1时,则试件已发生疲劳损坏,此时试件的总共作用时间TF,即期望寿命:

在疲劳损伤频域分析方法中,应力峰值期望循环次数E [n(y1)]的估计在处理随机应力疲劳问题的能力上起关键作用。
4 结束语
近年来,多轴随机载荷下疲劳寿命的预测日益引起人们的重视,但因为问题本身的复杂性使得对该研究仍处于数据累积阶段,大量的试验研究有待进一步深入。
振动循环计数是随机载荷下疲劳损伤计算的基础。雨流计数方法几经修正完善,能够实现对多轴载荷下循环的计数。Dirlik经验公式从功率谱密度估计雨流计数法,具有一定的物理背景,因此愈来愈受到各国学者的重视,结合多轴疲劳损伤分析的能量法以及Miner的线性损伤规律是目前多轴随机振动载荷疲劳损伤分析中常用的方法。
(
)
[1] 陈颖, 朱长春, 李春枝, 等. 某结构的多轴随机振动实验研究[J]. 实验力学, 200924(1): 35-41
[2] 樊世超, 冯咬齐. 多维动力学环境模拟试验技术研究[J].航天器环境工程, 2006, 23(1): 23-28
[3] 高桦. 多轴疲劳研究[J]. 机械强度, 1996, 18(1): 9-13
[4] Pitoiset X, Preumont A. Tools for a multiaxial fatigue analysis of structures submitted to random vibrations[J]. Journal of Vibration and Acoustics, 1994, 45(3)
[5] Spottswood S M, Wolfe H F. Comparing fatigue life estimates using experimental and spectral density based probability distributions[R]. American Institute of Aeronautics and Astronautics, 2001, 22(5): 155-162
[6] Adam Niesłony. Comparison of some selected multiaxial fatigue failure criteria dedicated for spectral method[J]. Journal of Theoretical and Applied Mechanics, 2010, 48(1): 233-254
[7] Langlais T E, Vogel J H, Chase T R. Multiaxialcycle counting for critical plane methods[J]. International Journal of Fatigue, 2003, 64(5): 51-64
[8] Chen X, Jin D, Kim K S. Fatigue life prediction of 304 stainless steel under sequential biaxial load[J]. Int Fatigue, 2006, 28(3): 176-187.
[9] Bishop N W M, Sherratt F. A theoretical solution for the estimation of rainflow ranges from power spectral density data[J]. Fatigue Fract Engng Mater Stuct, 1990, 13(4)
[10] 金丹, 陈旭. 多轴随机载荷下的疲劳寿命估算方法[J].力学进展, 2006, 36(1): 65-74
[11] 尚德广. 多轴疲劳损伤与寿命预测研究[D]. 西南交通大学博士学位论文, 1995

