相贯线在数控加工中的解析求法
王晓雪
(山西大同大学工学院,山西大同 037003)
在我们的生活和生产中,常常会遇到两个或若干个立体相交的问题(在画法几何中,我们称之为相贯),比如在机械生产、化工设备、运输管道、钢结构构件的连接中,通常会遇到一些平面与曲面立体之间的截交以及曲面立体曲面立体之间的相贯问题.而通常我们只用作图法来求,作图法虽然形象、直观、迅速,但却由于受到作图操作和仪器工具的限制,再加之作图过程繁顼、图形绘制不准确,往往给生产制作造成许多麻烦,且精度更不能满足现代技术与计算机辅助设计和数控制造技术的要求,因此这我们采用图解与计算相结合的方法,通过投影图上的几何关系,再利用解析方法,建立相贯线上点的坐标方程或极坐标方程.并根据所求的坐标方程或极坐标方程,在数控机床上利用切割工具,切割出我们所需的各种相贯曲线.为此建立相贯线上的点的坐标方程或极坐标方程是非常重要的.
1 两圆柱体相贯
如图1所示为轴线相交的两圆柱体相贯[1-2](正立投影),现用作图与解析相结合的方法来求相贯线.
设两圆柱的底面半径分别为r1与r2(均已知),两圆柱轴线的交点为o,它们之间的夹角为δ(已知),以o为原点,分别建立各自的三维坐标体系,y1轴垂直于x1oz1平面,y2轴垂直于x2oz2平面,而x1oz1和x2oz2正好在同一平面内,所以y1与y2为同一条轴,其坐标我们均计为y,由图1的几何关系可得下面解析式[3-4]:
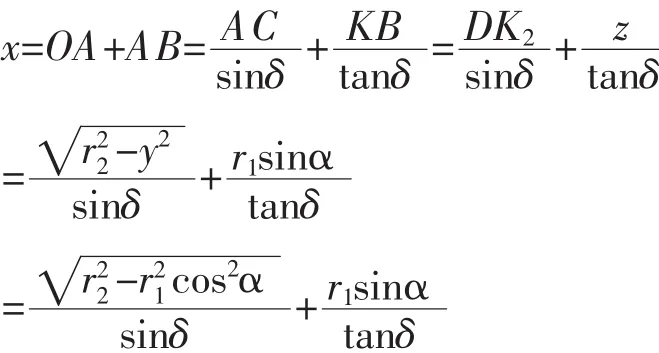
在制作该相贯线时,可将圆柱面展开成板,横坐标为α,纵坐标为x,在数控机床[5]上用数控线切割机按坐标便可加工出所需曲线.
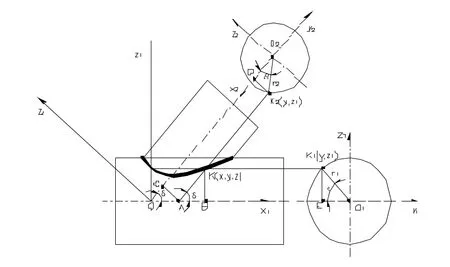
图1 圆柱体与圆柱体相贯图
2 圆柱体与圆锥体相贯
如图2所示为轴线相交的圆柱体与圆锥体的相贯[1-2],圆锥顶角为圆柱体的中心轴线与x轴的夹角为且其中心轴线与圆锥中心轴线相交.坐标如图2所示,则圆柱曲面方程[4]为:
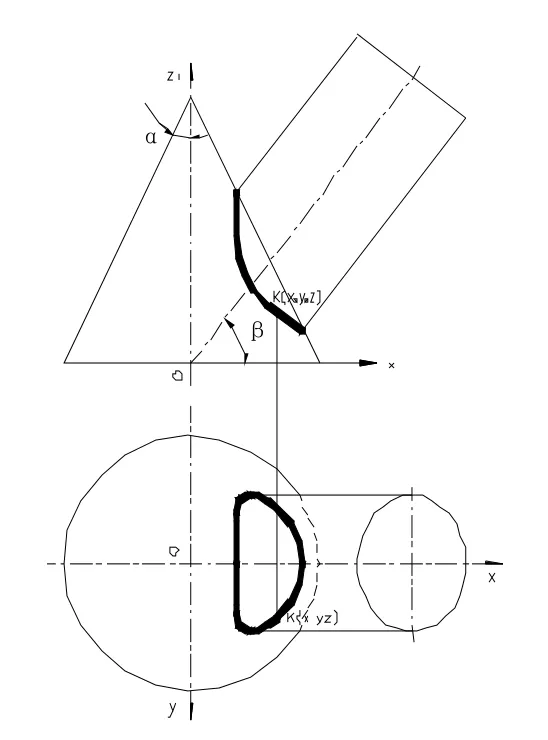
图2 圆柱体与圆锥体相贯图
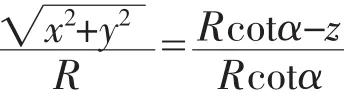
即:

圆柱曲面方程[4]为:
即

设 x=ρcosθ,y=ρcosθ,这里 0<θ<2π,(ρ<R)代入上面(1)、(2)两方程并联立解,便可得两立体相贯线的方程[4]为:
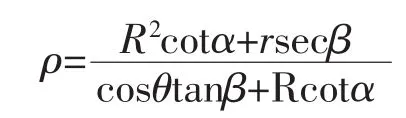
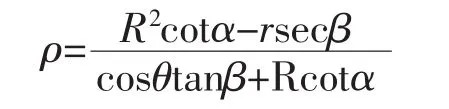
上式即为相贯线上任一点的极坐标方程,在制作时将圆锥面展开成板,用数控线切割机按该极坐标方程即可加工成形[5].
对于任何平面与立体截交以及立体与立体相贯,都可求出其解析方程,使我们在数控机床的生产中,可以根据相贯线的曲线方程来控制切割工具的运动走向,致使在机床上加工出我们所需的各种曲线,且克服了由于作图而产生的误差,并能更好地满足日益发展的计算机辅助设计和制造技术的需要.
[1]何铭新,钱可强.机械制图[M].北京:高等教育出版社,1997:117-132.
[2]同济大学建筑制图教研室编著.画法几何[M].上海:同济大学出版社,1984:45-50.
[3]樊映川.高等数学讲义[M].北京:高等教育出版社,1986:137-164.
[4]高红铸,傅若男.空间解析几何[M].北京:北京师范大学出版社,2007:137-164.
[5]何伟.数控机床原理及应用[M].北京:机械工业出版社,2007:107-124.

