单级倒立摆LQR控制方法的鲁棒稳定性分析
刘微微,张 静
(哈尔滨理工大学 自动化学院,哈尔滨 150080)
0 引 言
对于单级倒立摆系统,目前已有多种控制方法可对其实现稳摆控制。典型的有线性 PID控制[1-2]、常规PID控制[3]、LQR控制、智能控制[4]等。其中,LQR控制方法的优势在于其控制方案简单,超调量小,且响应速度快,该方法不仅对单级倒立摆系统能够进行有效控制,且已经成功地应用于直线双倒立摆[5]和双足机器人[6]的控制。
鲁棒稳定性是衡量控制系统控制品质优劣的一个重要指标[7],鉴于LQR控制方法已有的控制优势,有必要对该控制方法的鲁棒稳定性做详细分析,以进一步验证LQR控制方法的控制优势。本文针对单级倒立摆系统,完成了系统建模及LQR控制的MATLAB仿真,通过增加系统自身的扰动及LQR控制器中加权阵R的改变考察该控制方法的鲁棒稳定性,对比仿真结果表明该控制方法鲁棒稳定性良好。在较大的系统参数摄动下系统达到稳态的时间变化较小。
1 单级倒立摆系统建模
单级倒立摆的控制目标是:由倒摆和小车组成的倒立摆在适当的控制力作用下,在有限长度的导轨上,受到干扰后,倒立摆仍然能够竖直立稳[8],即θ≈0,且小车位移x≈0(图1)。
实际的单级倒立摆系统比较复杂,除了各组成器件的非线性外,还受到各种干扰,为分析其本质,需要对实际系统进行简化[9]。简化约束条件如下:
1)将摆杆视为质量均匀分布的刚体细杆;
2)各部分的摩擦力与相对速度成正比;
3)施加在滑块上的驱动力与加在功率放大器上的输入电压成正比,并无延时地施加到滑块上;
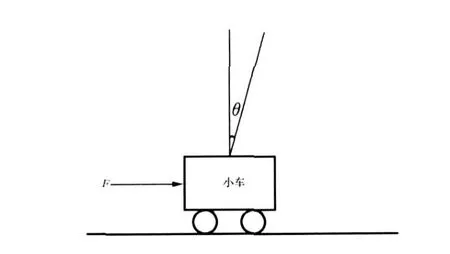
图1 倒立摆系统示意图Fig.1 Schematic diagram of inverted pendulum system
4)皮带轮与传送带之间无滑动,传送带无伸长现象;
5)除滑块与导轨之间的摩擦及摆杆转轴的摩擦外其它摩擦及阻尼的影响均忽略。
设摆杆偏离垂直线的角度为θ,同时规定摆杆重心的坐标为(xG,yG),则有:

根据牛顿定律,建立水平和垂直运动状态方程。
摆杆围绕其重心的转动运动可用力矩方程来描述:
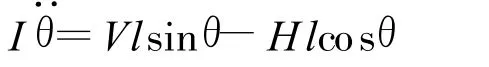
式中I为摆杆围绕其重心的转动惯量。
摆杆重心的水平运动由下式描述:

摆杆重心的垂直运动由下式描述:
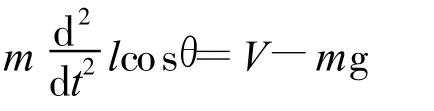
小车的水平运动由下式描述:

假设θ很小,sinθ≈θ,cosθ≈1。则以上各式变为:
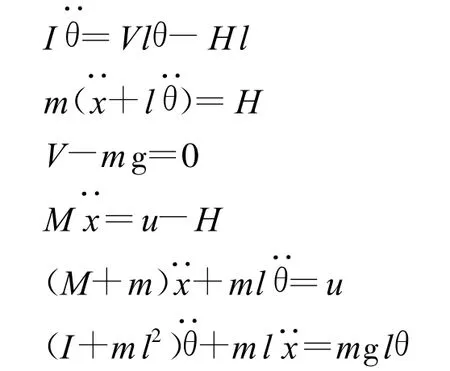
得到的单级倒立摆方程为:
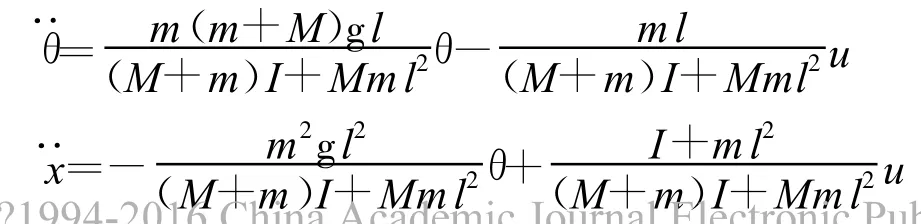
控制指标共有4个,即单级倒立摆的摆角θ、摆速˙θ、小车位置x和小车速度˙x。将倒立摆运动方程转化为状态方程的形式。令x(1)=θ,x(2)=˙θ,x (3)=x,x(4)=˙x,则状态方程式为:
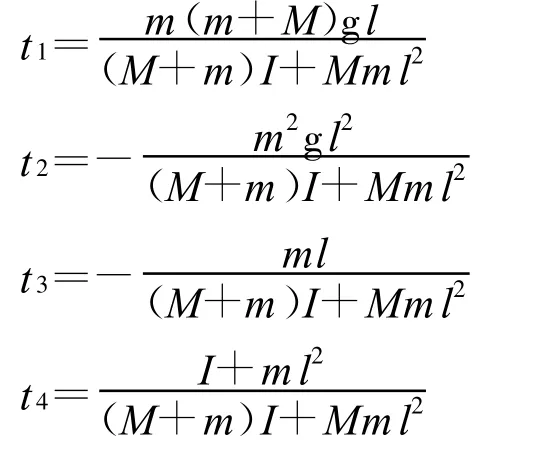
2 单级倒立摆系统LQR控制
LQR方法[10]针对状态方程˙x=Ax+Bu,通过确定最佳控制量u(t)=-K x(t)的矩阵K,使得控制性能指标达到极小,其中Q为正定(或半正定)厄米特或实对称矩阵,R为正定厄米特或实对阵矩阵,Q和R分别表示了误差和能量损耗的相对重要性,Q中对角矩阵的各个元素分别代表各项指标误差的相对重要性。LQR控制器的增益为:
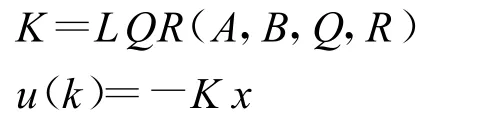
3 MATLAB环境下的单级倒立摆系统LQR控制仿真
倒立摆参数选取:
取重力加速度g=9.8 m/s2;
小车质量M=1.0 kg;
杆的质量m=0.1 kg;
半杆长L=0.75 m;
小车相对于导轨的摩擦系数μc=0.000 5;
杆相对于小车的摩擦系数μp=0.000 002;
小车控制力F,即控制力的输出,在[-10,10]上连续取值。采样周期T=10 ms。
初始条件取θ(0)=-10,˙θ(0)=0,x(0)= 0.15,˙x(0)=0,期望状态为θ(0)=0°,˙θ(0)=0, x(0)=0,˙x(0)=0。
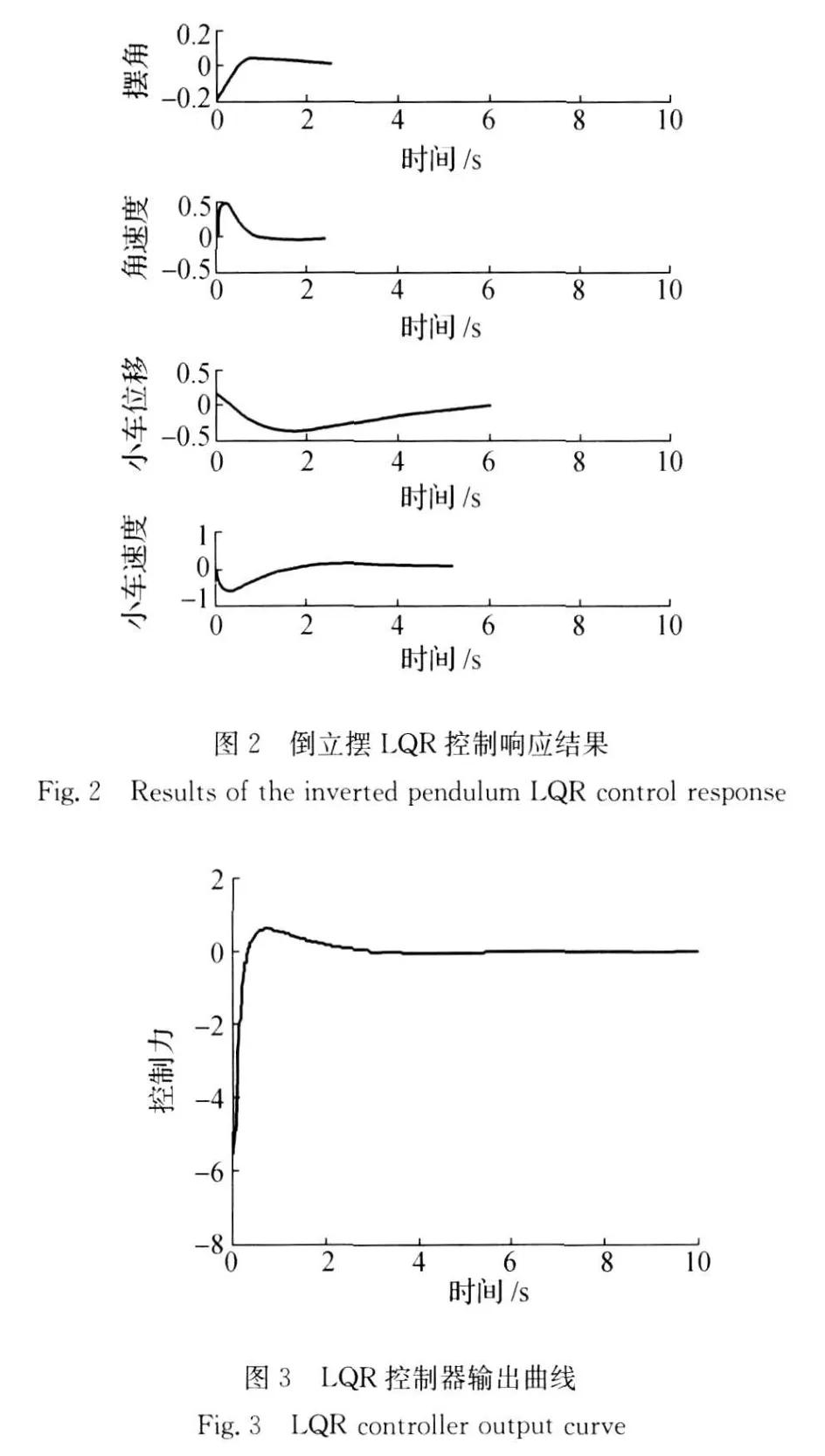
仿真结果见图2,LQR控制器输出曲线见图3。
4 LQR控制方法鲁棒性分析
鲁棒性是衡量控制系统控制品质的重要指标,通过以上的仿真结果可以看出LQR控制方法是可行且有效的。对该方法的鲁棒性分析主要从以下3个方面进行:①改变小车质量和摆杆长度;②改变初始摆角和小车位置;③改变Q和R的取值。
其中前两个方面是分析倒立摆系统自身扰动对控制效果的影响,即验证该方法的稳定鲁棒性;后一方面是分析控制器参数变化对控制效果的影响,即验证该方法的品质鲁棒性。
4.1 改变小车质量和摆杆长度
取M=1.090,L=0.25,m=0.13;此时的控制器增益变为K=(-33.542 3,-5.132 6,-1.000 0,-2.324 9)。
改变小车质量和摆杆长度后的响应结果见图4。
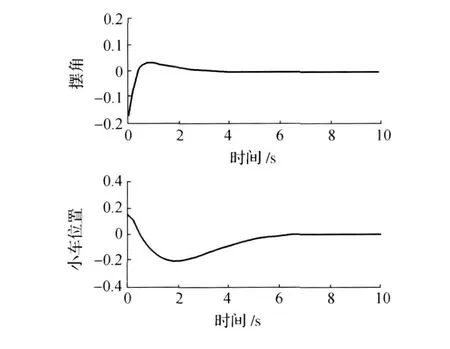
图4 改变小车质量和摆杆长度后的响应结果Fig.4 Response of changes in the pendulum length of the car
4.2 改变初始摆角和小车位置
取θ(0)=-20,˙θ(0)=0,x(0)=0.20,˙x(0)= 0;此时的控制器增益为 K=(-34.369 6, -7.911 3,-1.000 0,-2.411 3)。
改变初始摆角和小车位置后的响应结果见图5。
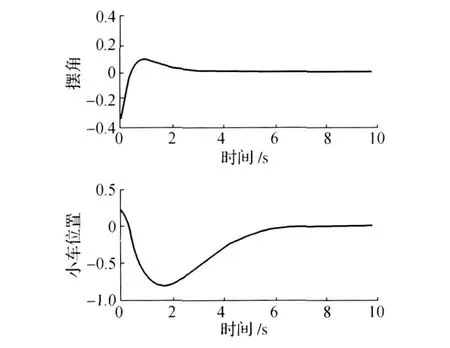
图5 改变初始摆角和小车位置后的响应结果Fig.5 Response of changes in the initial pendulum angle and the car
4.3 改变控制器中Q与R的值
采用LQR方法,关键是选择加权矩阵Q,一般Q越大,系统达到稳态的时间越短。这里选择一个较为理想的Q值,R值仍取1。
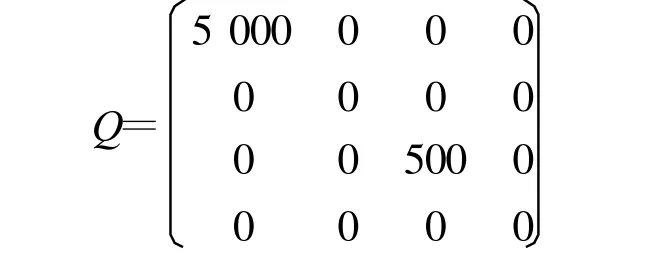
此时的控制器增益为K=(-120.170 0, -21.740 8,-22.360 7,-22.342 6)。
改变加权阵Q后的响应结果见图6,控制力输出曲线见图7。
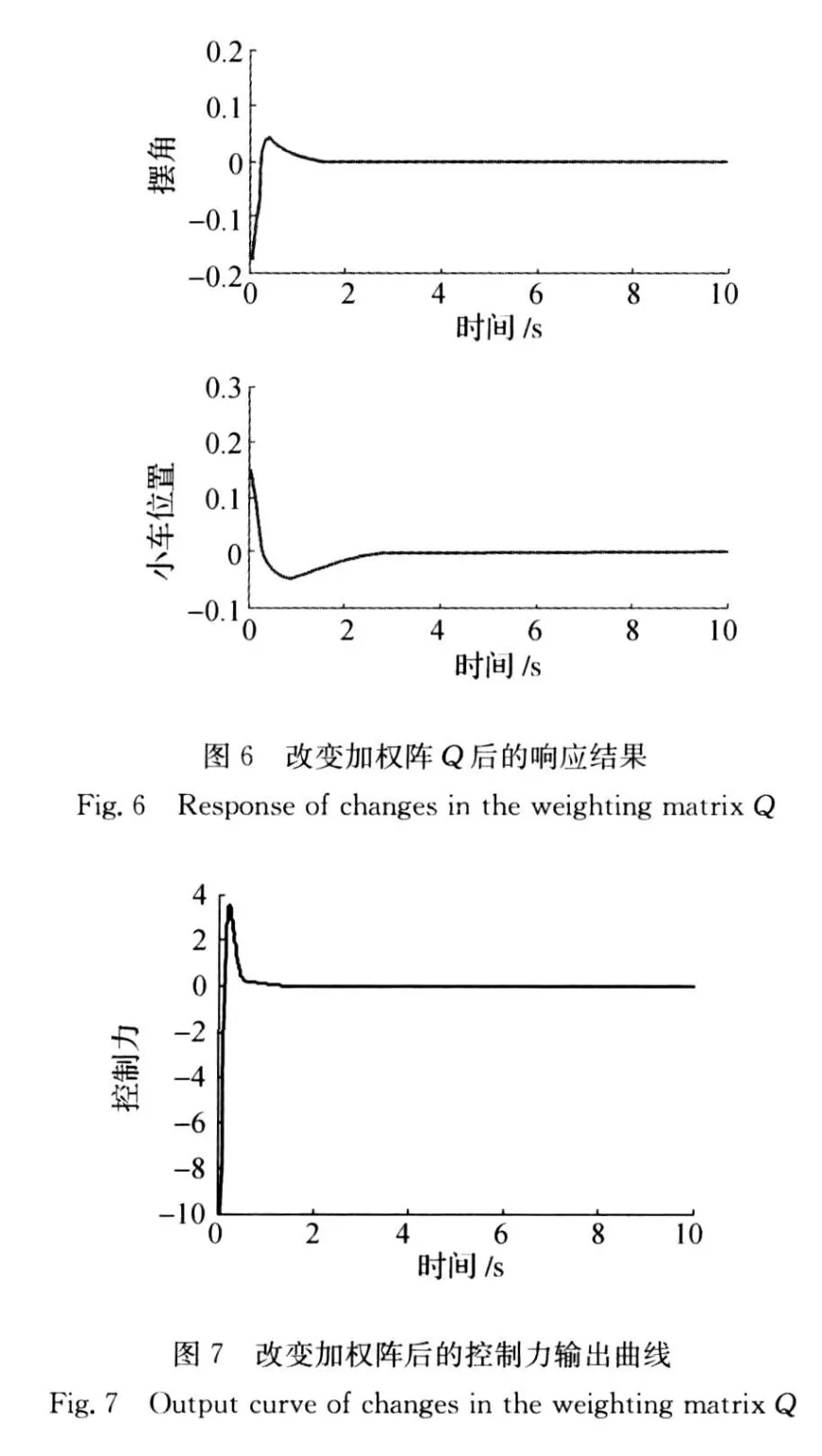
5 仿真实验结果分析
利用LQR方法可以成功实现对单级倒立摆的控制,小车位置x和摆角θ上升时间达到了0.8 s,过渡时间2.5 s,通过增加倒摆系统自身的扰动从3个方面分析了LQR方法的鲁棒性,对比仿真实验结果可以看出该方法具有较强的鲁棒稳定性,受到扰动后的倒立摆系统稳定性良好。增大加权阵Q使得系统达到稳态的时间控制在了1.5 s,且各情况下的摆角θ超调量均<25%。
6 结 论
鲁棒稳定性是衡量控制系统控制品质的重要指标,本文通过3组不同参数的变化考察了LQR控制方法的鲁棒稳定性。倒立摆系统是一个多变量、非线性、强耦合的绝对不稳定系统,采用常规的PID控制效果一般较差,主要因为常规的PID控制器实际上是一种线性控制器。本文针对单级倒立摆系统采用最优控制中的LQR控制方法,是对系统进行局部的线性化,通过仿真实验得到该方法作用于倒立摆系统是可行且有效的,在较大的系统参数摄动下依然能够保持系统的鲁棒稳定性。
[1] 桑英军,范媛媛.单级倒立摆两种控制方法的研究[J].科技信息,2009,(25):115-116.
[2] 邢景虎,陈其工,江 明.单级倒立摆的两种控制方法的仿真研究[J].工业仪表与自动化装置,2008,(2):7-9.
[3] 严雪莉,江汉红.单级倒立摆控制方法的仿真对比研究[J].测控技术,2005,24(7):37-39.
[4]陈 华.单级倒立摆智能控制器的设计[J].重庆工学院学报, 2009,23(1):98-101.
[5] 刘金亨,陈今润,吕郁青,等.基于LQR的一阶直线双倒立摆最优控制系统研究[J].自动化技术与应用,2009,28(5):11-13.
[6] 槐创锋,方跃法.5连杆双足机器人建模和控制系统仿真[J].系统仿真学报,2008,20(20):82-86.
[7] 赵英彪,荆武兴.柔性航天器单轴姿态机动的鲁棒稳定性分析[J].哈尔滨工业大学学报,2009,41(1):44-48.
[8] 李德毅,杜 鹢.不确定性人工智能[M].北京:国防工业出版社,2005.
[9] 姜春瑞.基于云模型理论的一阶直线倒立摆控制技术研究[D].哈尔滨:哈尔滨工业大学,2005.
[10] 刘金琨.先进PID控制及其M AT LAB仿真[M].北京:电子工业出版社,2004:324-330.

