模糊控制在光电稳定平台跟踪控制中的应用

毕永利,王中鲜

(1.哈尔滨工业大学 控制理论与制导技术中心,哈尔滨 150001;2.黑龙江大学 机电工程学院,哈尔滨 150080)

0 引 言

近几年来,光电稳定平台被广泛地应用于军事领域和公安、消防及环境监控等民用领域,它是一个集光、机、电于一体的复杂系统。目前较先进的光电稳定平台一般装有电视摄像机、红外热像仪、激光测距机3套探测设备,配置比较齐全,这样利用1台光电稳定平台就能实现全天候工作。平台在工作中:①要能隔离外界各种扰动(例如载体角振动、摩擦力矩、风阻力矩、线绕力矩、框架间耦合力矩、质量不平衡力矩等),保证平台中传感器视轴稳定;②要能跟随被跟踪的目标运动,使光电传感器视轴始终精确指向目标,以完成对目标的捕获、跟踪及测量。因此,光电稳定平台中稳定与跟踪控制精度是一项重要性能指标。目前,光电稳定平台控制系统设计一般采用基于经典控制理论的设计方法,在设计出校正装置的传递函数后,用冲激不变法、零阶保持器法或双线性变换等方法,将连续的校正装置传递函数离散化,从而获得相应的数字控制算法。在速率稳定环采用经典控制理论的基础上,在跟踪环中本文提出了一种基于遗传算法的模糊控制策略,充分利用了模糊控制不需要建立被控对象的精确数学模型,且控制灵活,鲁棒性强,具有逼近任何非线性函数能力的特点,并通过仿真验证了该方法的可行性和有效性,为光电稳定平台跟踪精度的提高进行一种有益的尝试。

1 跟踪方式下控制系统组成

光电稳定平台的跟踪模式一般分为手动跟踪和自动跟踪两种方式。手动跟踪方式是通过操作手操纵单杆对感兴趣的目标进行跟踪、测量及辨识,跟踪精度的高低取决于操作手的熟练程度。自动跟踪方式是在跟踪器捕获目标后,根据其给出的脱靶量进行跟踪,跟踪精度取决于跟踪控制器的性能。因此,可以设想利用熟练操作手的丰富经验,提炼出控制思想(语言),利用模糊控制所具有的特点,完成自动跟踪控制器的设计。多传感器、多框架光电平台在自动跟踪方式下控制系统的组成框图见图1。

它由电视跟踪器、红外跟踪器、电视和红外信号正割补偿环节、电视和红外跟踪回路校正放大、速率稳定回路校正放大、PWM环节、被控对象、陀螺信号预处理、A/D采集、陀螺信号正割补偿等环节组成。

图1 自动跟踪方式下控制系统框图Fig.1 Block diagram of control system under automatic tracking mode

2 模糊控制器设计

自动跟踪方式下基于遗传算法的跟踪环模糊控制器结构见图2。

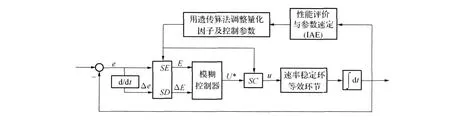
图2 基于遗传算法的模糊控制器框图Fig.2 Block diagram of fuzzy controller based on GA

图中偏差e及其微分△e通过比例因子SE和SD调整后,作为模糊控制器的两个输入变量E和△E。比例因子(SE、SD、SC)的调节是实现整个模糊控制器的关键,当模糊控制器控制策略确定后,可以通过遗传算法获得最优的比例因子。

现在建立一个模糊机。模糊控制器的输入、输出变量都是精确量,模糊推理是针对模糊量进行的,因此,控制器首先要对输入量进行模糊化处理。在所设计的模糊控制器中,输入变量(E和Δ E)均分为7个语言值:{NB、NM、NS、ZO、PS、PM、PB},子集中元素分别代表{-1、-2/3、-1/3、0、1/3、2/ 3、1}。隶属度函数采用灵敏性强的三角函数形式,见图3。因此,一个完整的模糊规则由49个IFTHEN语言构成。为简便起见,输出变量(U*)同样分为7个语言值:{NB(-1)、NM(-2/3)、NS (-1/3)、ZO(0)、PS(1/3)、PM(2/3)、PB(1)},其隶属度函数见图4。

模糊控制设计是总结工程技术人员的知识和实际操作经验,参数的整定规则是控制器的核心,需要建立合适的模糊整定规则表。本文建立了一种对称的模糊整定规则表,见表1,其中m3、m2和m1分别为1、2/3和1/3。

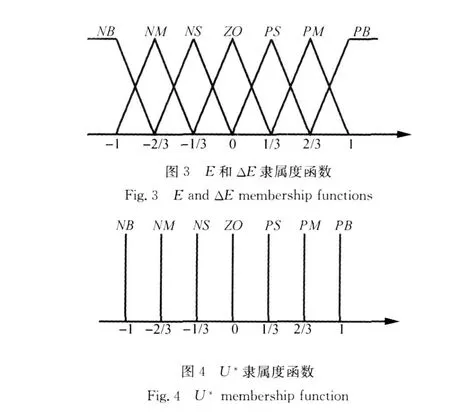
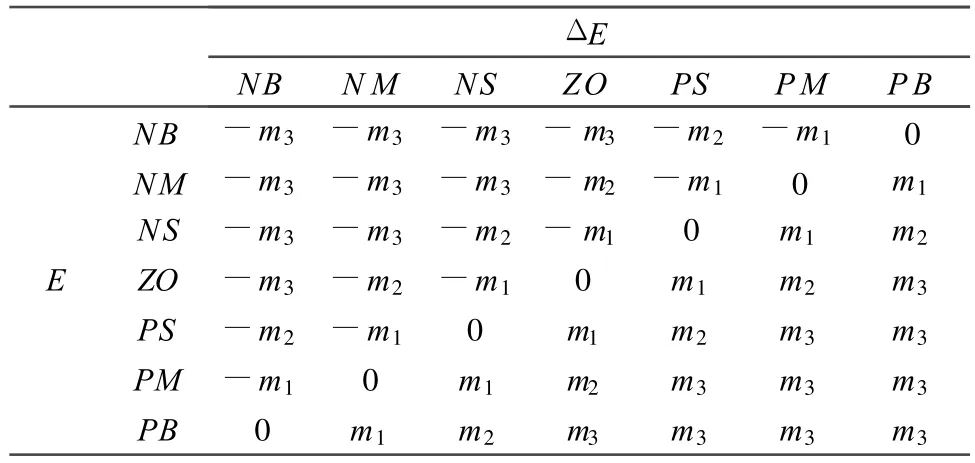
表1 对称的模糊整定规则表Table 1 Symmetric fuzzy regulation

对输入的偏差E及其微分 Δ E,在取得相应的语言值后,根据整定规则表,经过模糊推理后,将修正参数进行去模糊化取得精确量,以计算输出控制量。去模糊化有几种常用方法,如最大隶属度法、重心法等,对本文控制器,采用重心法求取输出量的精确值。

为了获得最优比例调节因子,采用遗传算法进行调节。遗传算法具体步骤为:

将初始数据简化为二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生越来越好的近似解。在每一代中,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。在这个过程中将导致种群像自然进化一样的吼声代种群比前代更加适应于环境,末代种群中的最优个体经过解码,就可以作为问题的近似最优解,具体流程见图5。

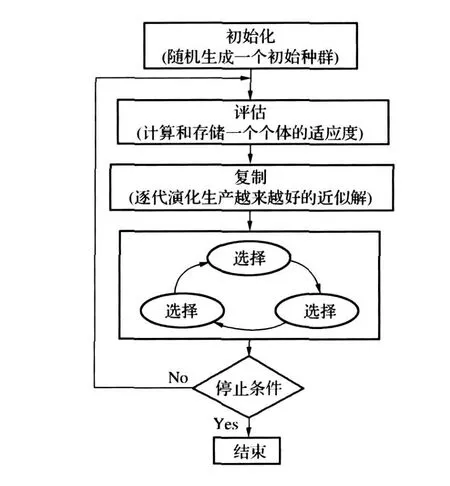
图5 遗传算法流程图Fig.5 Flowchart of genetic algorithm

为了获得最优的动态性能指标,采取IAE为最适应度函数(目标函数),即:J

3 仿真及分析

在速率稳定环良好设计的基础上,在仿真跟踪环时可将速率稳定环等效为小时间常数惯性环节。同时,要注意模拟跟踪器脱靶量处理、传输的延时以及脱靶量通讯传输速率等因素的影响。具体仿真参数如下:

;脱靶量总延时:φ=-4ω;遗传算法:初始种群数为30,交叉近似度为0.9,变异近似度为0.033,总代数为100;跟踪最大速度v=10°/s、最大加速度a=5°/s2;最大2个码均匀分布脱靶量量化噪声和随机扰动。稳态跟踪误差(RMS)＜0.05°。在考虑模糊控制策略时,采用了可变论域,当位置误差接近系统精度要求时,自动切换到小论域进行控制,以提高稳态性能。跟踪误差曲线见图6。最大跟踪误差0.072°,最小跟踪误差-0.074°,稳态跟踪误差(RMS)0.039°。可见,满足系统性能指标要求。

图6 跟踪误差曲线Fig.6 Curve diag ram of tracking error functions

4 结 语

仿真结果表明,基于遗传算法的模糊控制策略用于光电稳定平台跟踪环控制系统是完全可行的,其跟踪性能优于经典控制算法,且对被控对象模型的变化不敏感,具有更好的鲁棒性。为了得到性能更好的模糊控制器,应当通过对真实系统的实际操作得到准确的系统描述语言、隶属函数和控制规则。

[1] 赖小明,刘洁瑜.光纤陀螺稳定平台调平系统设计[J].计算机测量与控制,2007,15(3):363-365.

[2] 韩晓泉,陈 娟,王建立,等.光电跟踪中模糊控制的应用现状及发展[J].电光与控制,2003,10(2):58-61.

[3] 车 宏,卢广山.模糊控制在机载光电跟踪系统中的应用[J].电光与控制,2001,8(4):15-20.

[4] STEVEN J H,LA RRY A S,DOUGLAS E C,et al.Acquisition,Tracking and Pointing System for Self Protection Applications[J].SPIE,1998.