C/A码频域多普勒搜索FFT捕获算法＊

张 博,杨 春

(中国工程物理研究院 电子工程研究所,四川 绵阳 621900)

1 引 言

在高速环境中, GPS信号产生很大的多普勒频移,在没有星历信息、速度信息辅助的情况下,进行C/A码捕获是一大挑战。在传统的GPS接收机中,输入数字中频(IF)信号和某个多普勒频移的正弦和余弦分别相乘,变成基带信号,而后进行相关积分运算。相关积分可用滑动相关法和快速傅里叶变换(FFT)实现的循环相关方法[1]。由于FFT捕获方法在频域并行搜索所有伪码相位,速度较快,被越来越多的GPS接收机所采用。上述GPS接收机的多普勒搜索是在时域完成的,本文在FFT捕获方法基础上提出采用频域多普勒搜索,捕获速度可以加快一倍,甚至更多。由于预检测积分函数关于多普勒偏移呈现sinc函数特性[2],在两个相邻多普勒搜索之间的部分,预检测积分函数下降(损耗)较多,通过实行不同的下变频,有效地解决了频率分量间损耗的问题。

2 频域多普勒搜索

在FFT实现的循环相关捕获方法中,多普勒搜索大多数在时域内进行,如图1所示。输入IF信号和本地生成的某个多普勒偏移的正弦和余弦分别相乘后进行FFT运算,和本地伪码FFT的共轭相乘后进行快速傅里叶逆变换(IFFT)运算,得到这个多普勒搜索单元下的关于某颗GPS卫星所有伪码相位的相关函数。对每个多普勒单元逐一搜索,完成一颗GPS卫星的捕获。

离散傅里叶变换(DFT)具有频移特性,即时域内和复指数序列相乘等价于离散傅里叶变换的圆移。公式表示为

式中, X(k)为 x(n)的离散傅里叶变换(DFT),RN(n)为长度为N的矩形窗序列。

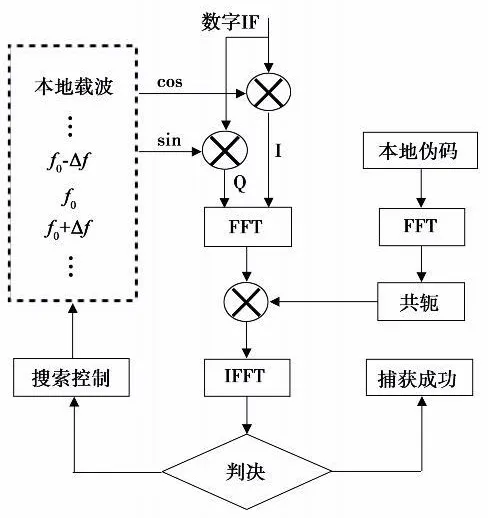
图1 时域多普勒搜索Fig.1 Time-domain Doppler search

利用这个特性,只需进行一次输入数字IF信号的FFT运算, 多普勒搜索通过圆移其频率分量完成,如图2所示。把圆移后的频率分量和本地伪码的FFT的共轭分别相乘后进行IFFT运算,得到这个多普勒搜索单元下的关于某颗GPS卫星所有伪码相位的相关函数。

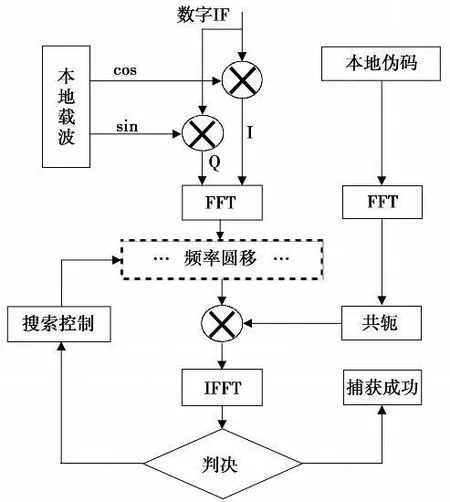
图2 频域多普勒搜索Fig.2 Frequency-domain Doppler search

待搜索的多普勒单元数为NDoppler,采用传统的时域多普勒搜索的FFT捕获方法,需要进行的FFT/IFFT计算次数为1(本地伪码)+NDoppler(混频后的数字IF)+NDoppler(IFFT)=1+2 NDoppler;采用频域多普勒搜索的FFT捕获方法,需要的计算次数为1(本地伪码)+1(混频后的数字IF)+NDoppler(IFFT)=2 +NDoppler。在高动态环境中, NDoppler很大(数百),相对于时域多普勒搜索的FFT捕获方法,频域多普勒搜索的FFT捕获方法大大减少了FFT的运算次数,捕获速度可提高一倍。由于时域内剥离多普勒频率实现方式的不同,捕获速度提高可能更多,对高动态GPS接收机来讲,这个提高是相当可观的。

3 频率分量间损耗的恢复

接收到的GPS信号可以表示为

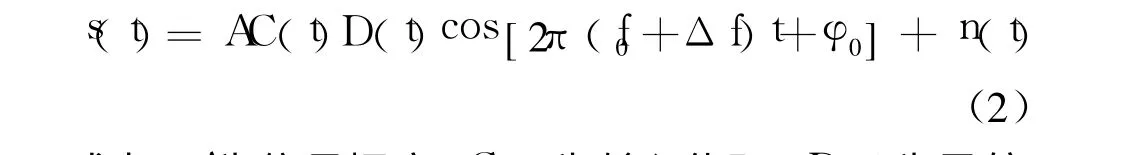
式中, A为信号幅度, C(t)为输入伪码, D(t)为导航数据, n(t)为加性带通噪声, f0为载波频率, Δf为由多普勒等引起的载波偏差, φ0为初始载波相位。

本地生成的同相、正交相参考信号表示为

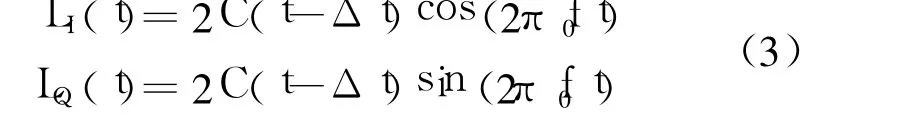
式中, Δt是本地伪码和输入伪码之间的时间误差。

把输入信号和本地信号相乘,滤除高频成分,生成基带信号,在一个导航数据位内对生成的基带分量进行预检测积分可得:

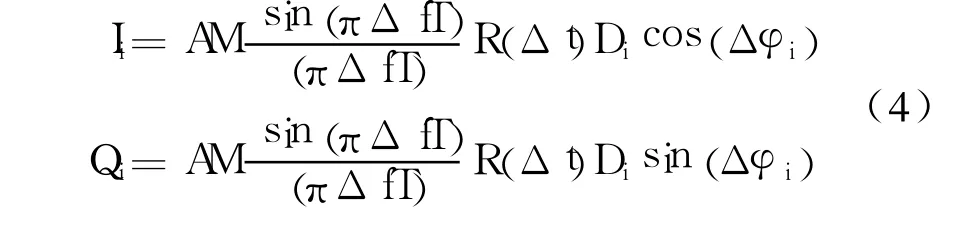
式中, M为在导航数据位Di历时T内的采样点数,Δφi为初始相位误差常数, R(Δt)为理想伪码之间的相关函数。

从预检测积分公式可以看出,由多普勒等引起的载波偏差对预检测积分输出引入了损失因子sin(πΔfT)/πΔfT,当ΔfT分别取0、0.25、0.5、0.75和1时,损失因子为1、0.9、0.64、0.3和0,当ΔfT>1/2时,损失将超过50%,这就是为什么GPS C/A码捕获要进行多普勒搜索的原因。

对于GPSC/A码,当积分长度为1 ms,本地载波频率为输入数字IF时,频域多普勒搜索算法搜索的 多 普 勒 单 元 中 心 频 率 为0, ±1 kHz, ±2 kHz, … ,若某个输入多普勒频率正好落在两个搜索频率中间,其幅度下降在弱信号捕获时这样的损失是不能容许的。采用加窗法(汉明窗或汉宁窗)进行补偿, 可以改善约2.3 dB。通过在两个输出频率分量之间产生一个新的频率分量[ 3 ] , 可以改善约3 dB, 如图3所示。但是,在nK+250, (n+1)K-250 Hz较大范围内, 相关幅度都下降约1 dB。

图3 频率分量补偿Fig.3 Frequency component compensation

为此,提出一种新的解决方案。采用两种本地载波信号进行下变频,第一种本地载波频率为fIF,可以搜索的多普勒单元中心频率为0, ±1 kHz, ±2 kHz, … ;第二种本地载波频率为fIF+500,可以搜索的多普勒单元中心频率为±0.5 kHz, ±1.5 kHz, … 。这两种方法的综合结果如图4所示,当输入频率恰好落在两个搜索频率中间时,其幅度下降

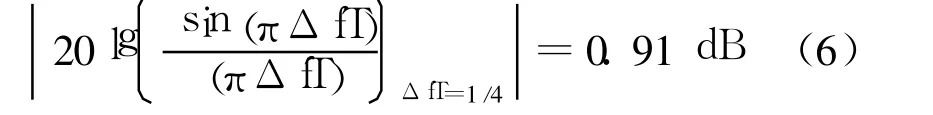
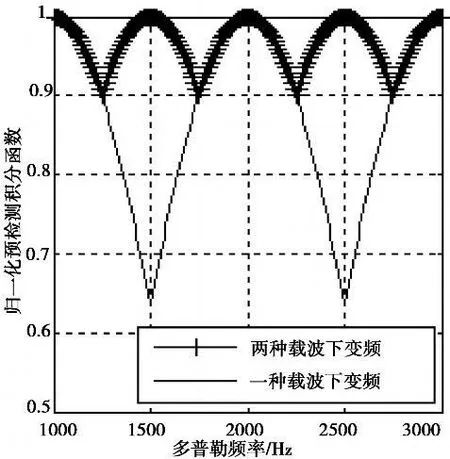
图4 新解决方案Fig.4 New app roach

若在时域进行多普勒搜索,把搜索步进频率由1 kHz减小到500 Hz,其相关幅度输出和本文提出的频域多普勒搜索方案结果相同,而时域多普勒搜索需进行FFT/IFFT计算次数为1+2 NDoppler,频域多普勒搜索需要的计算次数为3+NDoppler。

一般说来,积分长度为τintegrate,要获得Δf的多普勒频率精度,在时域进行多普勒搜索,搜索步进频率为 Δf, 需要进行的FFT/IFFT计算次数为1 +2 NDoppler;在频域进行多普勒搜索, FFT/IFFT计算次数为1+NDoppler+1/Δfτintegrate,这两种方法得到的相关幅度输出是相同的。

4 仿真结果

采用MATLAB对频域多普勒FFT捕获算法进行仿真,输入信号由软件GPS信号模拟器产生,信噪比为-19 dB,量化位数为3,数字中频为1.835 MHz,采样频率为6.144 MHz,预检测积分长度为1 ms。对5种典型多普勒频率进行仿真,图5 ～9中输入信号多普勒分别为1 000 Hz、1 250 Hz、1 500 Hz、1 750 Hz和2 000 Hz。对每种输入多普勒频率,采用3种多普勒估计进行运算,其中1 000 Hz和2 000 Hz由本地载波取fIF下变频后圆移生成, 1 500 Hz由本地载波取fIF+500 Hz下变频后圆移生成,分别对应5幅图中的(a)、(c)和(b)。从图中可以看出,当输入多普勒位于[1 000, 1 250] Hz时,采用多普勒估计1 000 Hz计算比较合适,对应图中的(a);当输入多普勒位于(1 250, 1 750)Hz时,采用多普勒估计1 500 Hz计算,对应图中的(b);当输入多普勒位于[ 1 750, 2 000] Hz时,采用多普勒估计2 000 Hz计算,对应图中的(c)。

图5 输入多普勒1 000 HzFig.5 Input Doppler 1 000 Hz

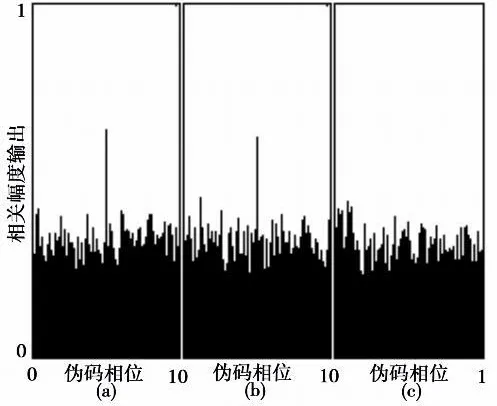
图6 输入多普勒1 250 HzFig.6 Input Doppler 1 250 Hz

图7 输入多普勒1 500 HzFig.7 Input Doppler 1 500 Hz

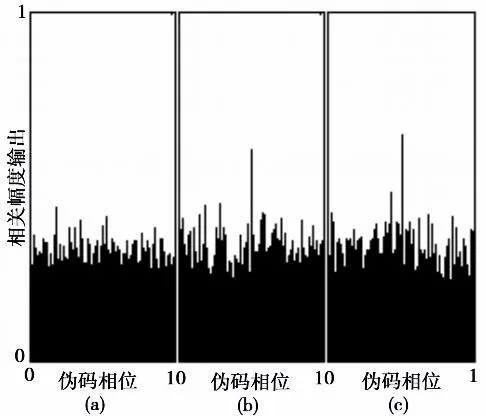
图8 输入多普勒1 750 HzFig.8 Input Dopp ler 1 750 Hz

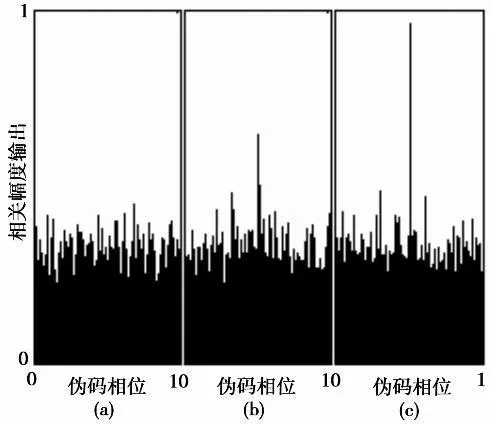
图9 输入多普勒2 000 HzFig.9 InputDoppler 2 000 Hz

5 结 论

分析表明,和时域多普勒搜索FFT捕获方法相比,采用频域多普勒搜索FFT捕获方法,捕获速度可提高一倍,甚至更多,具有很强的实用性。针对两个频率分量之间损耗较大问题,通过实行不同的下变频,有效解决了损耗问题。MATLAB仿真验证了频域多普勒搜索算法的正确性和频率补偿的有效性,频域多普勒搜索FFT捕获算法是一种快速、实用的捕获方案。

频域多普勒搜索算法不仅适用于GPSC/A码,也适用于其它直接序列扩频系统(DSSS)的伪码捕获。

[ 1] 张博,杨春,解楠,等.FFT快速捕获算法在GPSC/A码与P(Y)码中的应用[J].电讯技术, 2008, 48(12):34-38.

ZHANG Bo, YANG Chun, XIENan, etal.Application of FastFFT Acquisition Algorithm in GPS C/A and P(Y)Codes[J].Telecommunication Engineering, 2008, 48(12):34-38.(in Chinese)

[ 2] YANG C, VASQUEZ J, CHAFFEE J.Frequency-Domain Doppler Search and Jam-Suppression for Fast Direct P(Y)-Code Acquisition[C] //Proceedings of ION GPS.Nashville:[s.n.], 1999:317-324.

[ 3] JAMES BAO-YEN TSUI.GPS软件接收机基础[ M].陈军, 潘高峰, 等, 译.2 版.北京:电子工业出版社,2007:204.

JAMESBAO-YEN TSUI.Fundamentals of Global Positioning System Receivers:A Software Approach[ M].translated by CHEN Jun, PAN Gao-feng, et al.2nd ed.Beijing:Publishing House of Electronic Industry, 2007:204.(in Chinese)