单箱双室箱梁横隔板与横隔墙剪切应变能计算*
赵甲荐 魏德敏
(华南理工大学亚热带建筑科学国家重点实验室,广东广州 510640)
箱梁结构具有抗扭刚度大、能有效抵抗正负弯矩、适应现代化施工等优点.单箱双室箱梁更是以其整体性好、材料受力利用充分、景观效果好等优点,而在现代桥梁中得到广泛应用[1-2].由于箱梁截面畸变(扭转变形)、弯扭、翘曲变形以及剪力滞的存在,箱梁的结构分析变得十分复杂.在结构设计中,为了抵抗箱梁截面变形、增加截面的横向刚度、限制畸变应力,往往在梁跨中区域设置横隔板和在梁两端设置横隔墙.近年来,新建的大、中跨度预应力箱形梁桥越来越多,为减轻自重,箱形截面的壁越来越薄,甚至已发展到波纹钢腹板预应力箱梁[3-4],这大大降低了箱梁的抗扭刚度;此外,国内大量修建铁路和城市交通轨道,其桥梁结构大多采用箱梁,箱梁要承受列车或轨道车辆传来的超大荷载,产生的畸变应力很大.这都让箱梁横隔板和横隔墙的设置显得尤为重要,对横隔板和横隔墙受力性能的深入研究也更为迫切.
目前国内外有关设置横隔板和横隔墙来加强箱梁抗畸变能力的研究很多[5-6],但都没有研究横隔板和横隔墙的抗剪刚度与剪切应变能,而且方法简单,对其只做有限元计算或试验,没有理论推导.有学者对双 T型桥和单箱单室梁桥的横隔板和横隔墙的抗剪刚度与剪切应变能进行了研究[7-9],但没有对单箱双室梁桥的横隔板和横隔墙进行研究,并且对横隔板都只算了横向畸变角引起的剪切应变能,忽略了竖向畸变角引起的剪切应变能,有些推导的准确性有待证明.针对这些问题,文中从单箱双室箱梁畸变角的变位模式出发,研究横隔板横、竖向剪切应变能和横隔墙横向剪切应变能,并对横隔板开孔位置对抗剪刚度、剪切应变能的影响进行比较,为进一步的结构空间振动分析打下基础.
1 薄壁曲线单箱双室箱梁的位移模式
当箱梁截面发生畸变(扭转变形)时,产生很大的畸变应力,箱梁截面发生变形;此时,箱梁的顶、底板,左、中、右腹板挤压横隔板和横隔墙,迫使横隔板和横隔墙发生剪切变形,产生剪切应力,形成剪切应变能.要研究横隔板和横隔墙剪切应变能,必须先研究薄壁曲线单箱双室箱梁的位移模式.
对薄壁曲线单箱双室箱梁采用曲板板梁有限元单元法来进行空间计算分析.薄壁曲线单箱双室箱梁的实际截面如图 1所示,薄壁曲线单箱双室箱梁的截面计算简图与位移参数如图2所示.
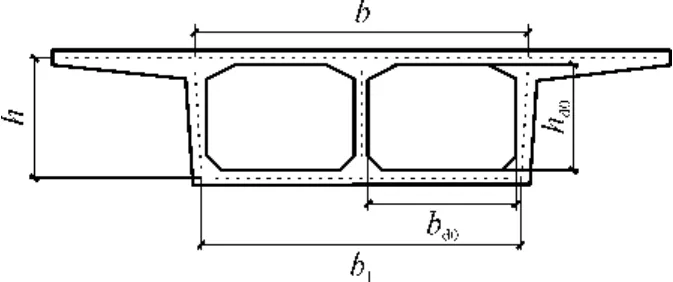
图1 单箱双室箱梁的实际截面Fig.1 Cross section of single-box double-cell box girder

图2 单箱双室箱梁的截面计算简图与位移参数Fig.2 Caculation diagram and displacement parameters of cross section of single-box double-cellbox girder
图中,bd0、hd0分别为箱梁单室的宽和高,也分别为单个横隔板或横隔墙的宽和高.截面位移参数包括4个角点的曲线切向位移值wul、wur、wll、wlr,箱梁顶板、底板的面内横向位移值uu、ul及左、右腹板上部竖向位移值vl、vr,共8个独立参数.两个非独立参数vlb、vrb分别为左、右腹板下部竖向位移,角 α为左、右腹板与竖线的夹角.
对曲线单箱双室箱梁的曲板板梁子单元,根据一般梁单元的基本假定,不考虑梁单元纵向纤维的挤压,可略去曲线单箱双室箱梁板件宽度与厚度方向纤维挤压变形.于是左腹板下部竖向位移为vlb=vl+(uu-ul)tgα,右腹板下部竖向位移为vrb=vr+(ul-uu)tgα.
2 单箱双室箱梁横隔板的剪切应变能
薄壁曲线单箱双室箱梁横截面畸变可分解为横向畸变和竖向畸变,设 γx、γy分别为箱梁横截面横向畸变角和竖向畸变角.
薄壁曲线单箱双室箱梁横隔板的实际截面如图3所示.单个横隔板开孔单向偏心,开孔位置任取.薄壁曲线单箱双室箱梁横隔板的截面计算简图如图4所示.
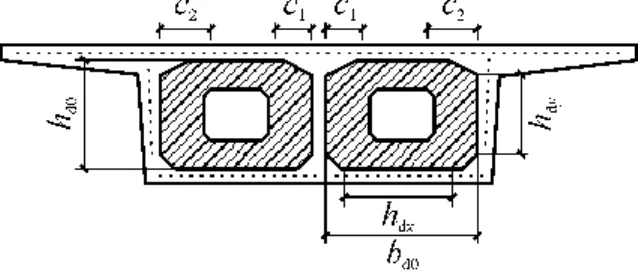
图3 横隔板的实际截面Fig.3 Cross section of diaphragm
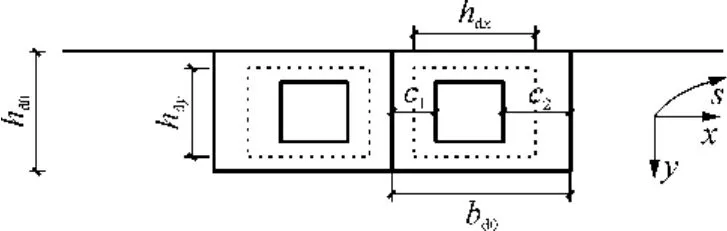
图4 横隔板的截面计算简图Fig.4 Caculation diagram of cross section of diaphragm
2.1 单箱双室箱梁横隔板的横向剪切应变能
根据一般梁单元的基本假定,当箱梁截面发生横向畸变时,横隔板可近似视为两个单跨竖立的具有无穷大刚度横梁的刚架,如图5所示.设Id1、Id2分别为单个刚架的两个刚架柱的弯曲惯性矩;设Rd为单个刚架的抗剪刚度,即刚架顶点产生单位横向水平位移时作用于顶点的横向水平力.
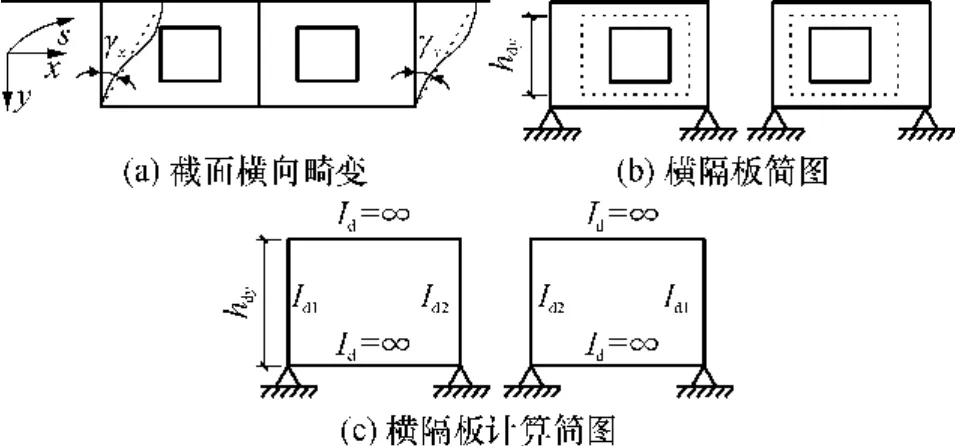
图5 横向畸变时的横隔板计算简图Fig.5 Transverse distortion caculation diagram of diaphragms
箱梁横截面横向畸变角 γx的变位模式有

式中:h为箱梁横截面顶、底板中线的距离.
由结构力学可求得单个刚架抗剪刚度:

式中:E为弹性模量;hdy为单个横隔板开孔上下两侧部分中心线的距离.
箱梁横截面两个横隔板的横向剪切应变能为
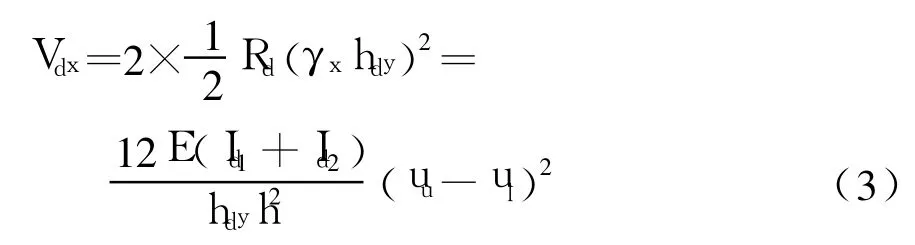
2.2 横隔板开孔位置对横向剪切应变能的影响
对于某个横隔板来说,开孔宽度一定,故令

式中:c1是单个横隔板靠中腹板部分的宽度;c2是单个横隔板靠边腹板部分的宽度;c0为一定值.
视单个刚架的两个刚架柱为杆件来求其弯曲惯性矩Id1、Id2,并将式(4)代入式(2),得
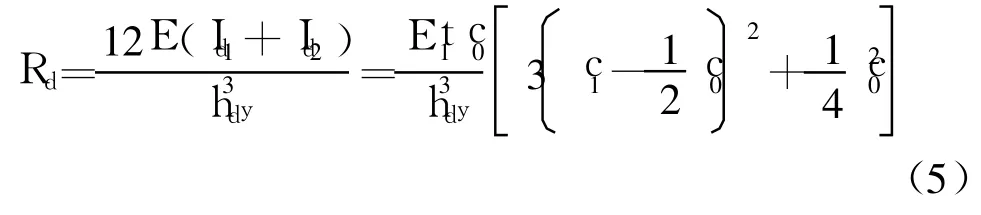
式中:t1为横隔板的厚度.
单个刚架抗剪刚度Rd与单个横隔板靠中腹板部分宽度 c1的理论关系曲线如图 6所示,由图 6可以看出:
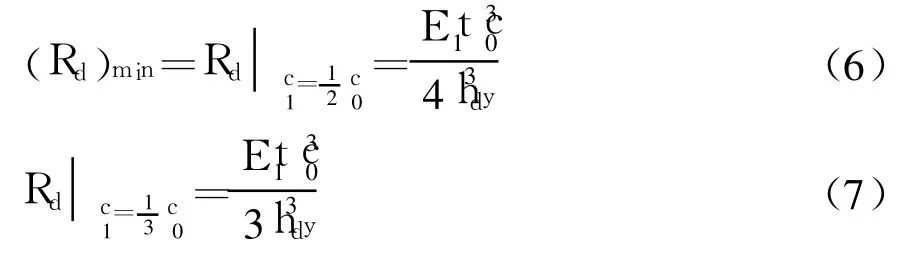
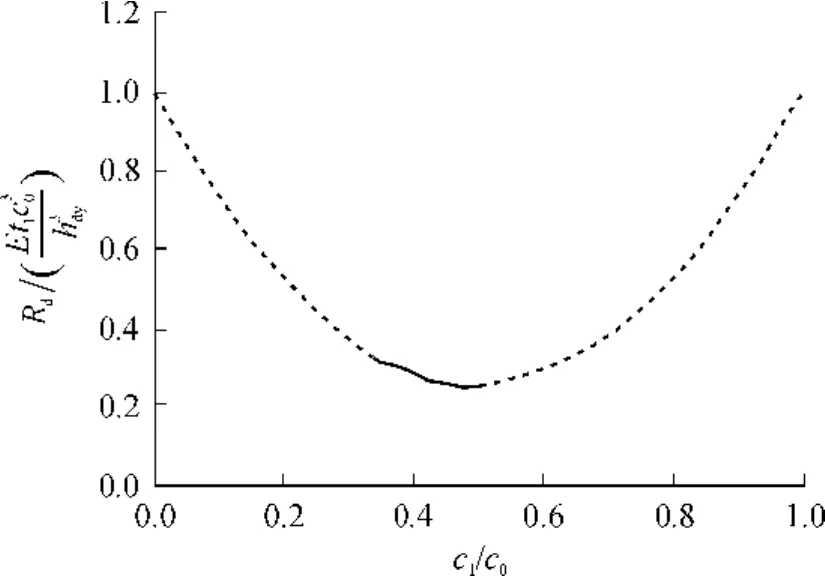
图6 Rd与c1的理论关系曲线Fig.6 Theoretical curve of Rd versus c1
下面讨论单个横隔板靠中腹板部分的宽度 c1的实际有效取值范围:
(1)截面中腹板两侧都有宽度为 c1的部分横隔板,而左右腹板只有内侧有宽度为 c2的部分横隔板.由于横隔板的作用,各个腹板旁边的部分横隔板都不能太单薄,所以c1≤c2,即c1≤0.5c0.
(2)c1=0或c1=c0大大减弱了横隔板抵抗箱梁截面变形的作用,实际操作中不允许,所以 c1≠0,且c1≠c0.
(3)当横向畸变比较小时,中腹板与两侧的部分横隔板一起变形,那么中腹板两侧部分横隔板合一起的宽度与左右腹板内侧部分横隔板的宽度最好相当,即c1=0.5c2=c0/3.在下面抵抗箱梁横截面竖向畸变时需要足够的刚度,故c1的值不能比此更小.
由此,单个横隔板靠中腹板部分的宽度 c1的实际有效取值范围为c0/3≤c1≤c0/2,即图 6所示的实线部分.单个横隔板的实际有效刚度取值范围为

由上述及式(3)可得出横隔板开孔位置对横向剪切应变能的影响:
(1)单个横隔板开孔位置变化范围为 0.5c2≤c1≤c2.
(2)横隔板中心开孔时的单个刚架抗剪刚度Rd最小,抵抗畸变的能力也最小.
(3)c1=0.5c2时的单个刚架抗剪刚度Rd最大,抵抗畸变的能力也最大,因此,靠近中腹板部分的横隔板宽度c1为靠近边腹板部分的横隔板宽度c2的一半时的横隔板单向偏心开孔是单箱双室箱梁横隔板开孔位置的最佳选择.
2.3 单箱双室箱梁横隔板的竖向剪切应变能
同理,当箱梁截面发生竖向畸变时,横隔板可近似视为两个单跨横卧的具有无穷大刚度横梁的刚架,如图 7所示.设I′d为单个刚架的单个横卧刚架柱的弯曲惯性矩.设 R′d为单个横卧刚架的抗剪刚度,即横卧刚架顶点产生单位竖向水平位移时作用于顶点的竖向垂直力.
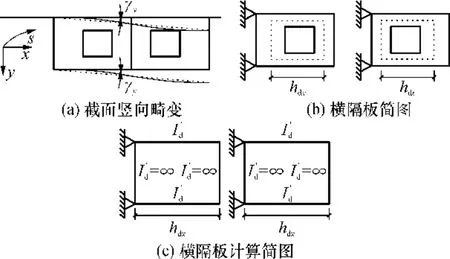
图7 竖向畸变时的横隔板计算简图Fig.7 Vertical distortion caculation diagram of diaphragms
箱梁横截面竖向畸变角 γy的变位模式有
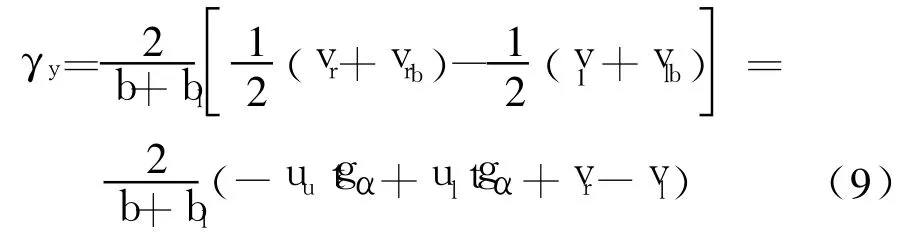
式中:b、bl为横截面左、右腹板中线在分别与顶、底板中线相交时两交点的距离.
由结构力学可求得单个刚架抗剪刚度(视横卧刚架柱为杆件可求其弯曲惯性矩I′d):

式中:hdx为单个横隔板开孔左右两侧中心线的距离.
箱梁横截面两个横隔板的竖向剪切应变能为
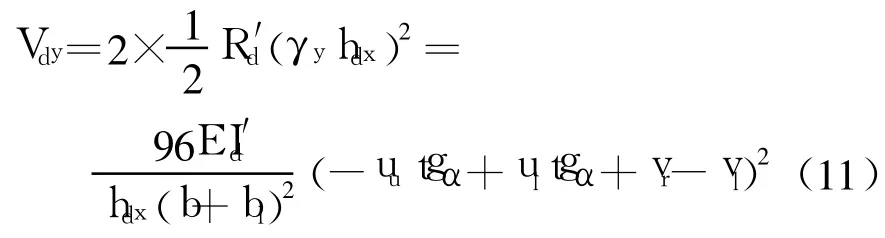
2.4 薄壁曲线单箱双室箱梁横隔板的总剪切应变能和平衡方程
结合式(3)和式(11),箱梁横截面横隔板的总剪切应变能为
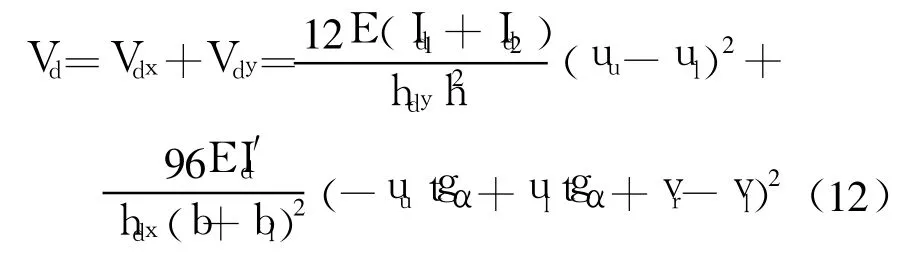
对式(12)取一阶变分,得,
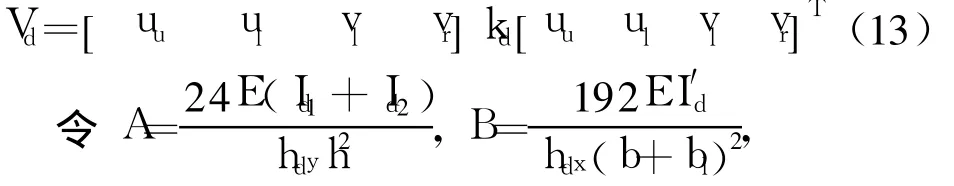
式中:kd为横截面横隔板的剪切刚度矩阵,

Vd为横截面横隔板的总剪切应变能的一阶变分; [uuulvlvr]T为箱梁横截面位移参数列阵; [uu,ul,vl,vr]为箱梁横截面位移参数的一阶变分行阵.
单箱双室箱梁截面横隔板的弹性总势能为两个横隔板所有弹性势能之和,即

式中:V为单箱双室箱梁截面横隔板的弹性总势能; F箱梁横截面荷载列阵;[uuulvlvr]为箱梁横截面位移参数行阵.
根据势能驻值原理与变分原理,得
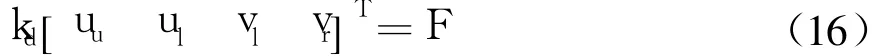
根据横隔板在单箱双室箱梁的位置,利用“对号入座”法[7]组拼到箱梁刚度矩阵中去,即可在整个箱梁的受力分析中考虑到横隔板刚度的影响.再进一步组拼到车-桥系统刚度矩阵中,可以完善车-桥系统空间振动分析.
3 单箱双室箱梁两端横隔墙的剪切应变能和平衡方程
略去曲线单箱双室箱梁板件宽度与厚度方向的纤维挤压变形,又由于梁端支座边界条件ul=vl= vr=wll=wlr=0,梁端横隔墙只有由uu引起的横向畸变,如图 8所示.单箱双室箱梁一端有两个横隔墙.
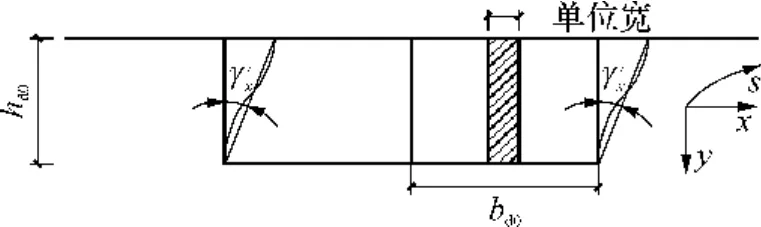
图8 横向畸变时的横隔墙计算简图Fig.8 Transverse distortion caculation diagram of side walls
箱梁端横截面横向畸变角为 γ′x,单个横隔墙的抗剪刚度为Rd0.γ′x的变位模式有

视单个横隔墙为板件来求其抗剪刚度.先对单个横隔墙随机取单位宽度横隔墙,由结构力学可求得单位宽度横隔墙的抗剪刚度,

式中:I1为单位宽度横隔墙的弯曲惯性矩;t2为横隔墙厚度;hd0为单个横隔墙高.
单个横隔墙的抗剪刚度
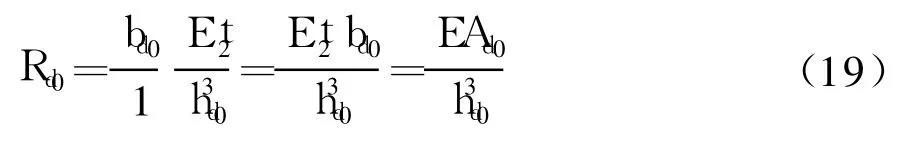
式中:bd0为单个横隔墙宽度;单个横隔墙水平横截面积为Ad0=t2bd0.
梁端两个横隔墙的横向剪切应变能为
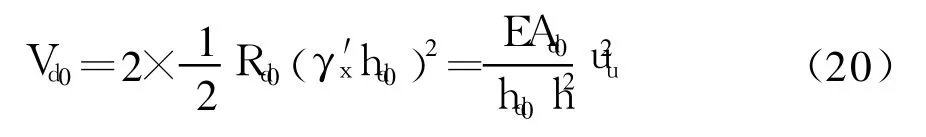
式中:Vd0为梁端两个横隔墙的横向剪切应变能的一阶变分;uu为箱梁端横截面顶板的面内横向位移的一阶变分.
梁端两个横隔墙的弹性总势能V′=Vd0-uuF′.其中:Vd0为梁端两个横隔墙的横向剪切应变能;F′为梁端横截面两个横隔墙所受的横向荷载.
根据势能驻值原理与变分原理,得

对式(20)取一阶变分,得,

根据梁端横隔墙在单箱双室箱梁的位置,利用“对号入座”法[7]组拼到箱梁刚度矩阵中去,即可在整个箱梁的受力分析中考虑梁端横隔墙刚度的影响.
4 算例与比较
4.1 算例
本文是新型轻轨车 -桥振动研究的前期工作,以上海明珠线为例.明珠线标准梁采用单箱双室截面、双柱式桥墩的预应力钢筋混凝土简支箱梁,跨度为30m,混凝土强度等级为C50.箱梁除两端设置端隔墙外,还沿纵向加设3道横隔板.为方便研究横隔板开孔位置对横向剪切应变能的影响,提供 3种横隔板的设计方案,尺寸如图 9所示.梁端横隔墙的尺寸如图10所示.横隔板、横隔墙厚度均为0.2m.材料动力弹性模量为4.2×107kN/m2,泊松比为0.16,重度为25kN/m3.
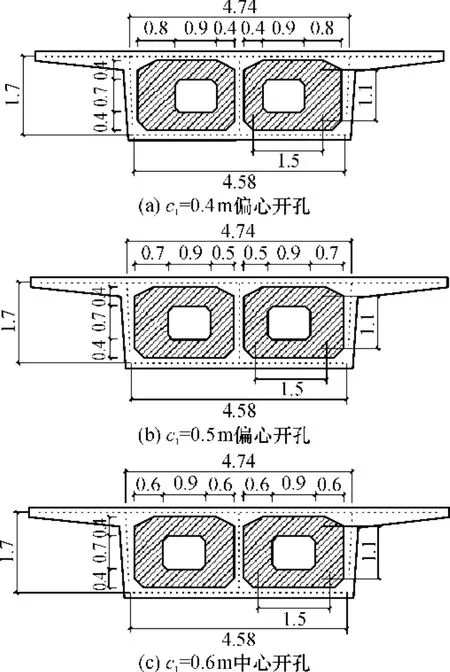
图9 横隔板尺寸(单位:m)Fig.9 Diaphragm size(Unit:m)
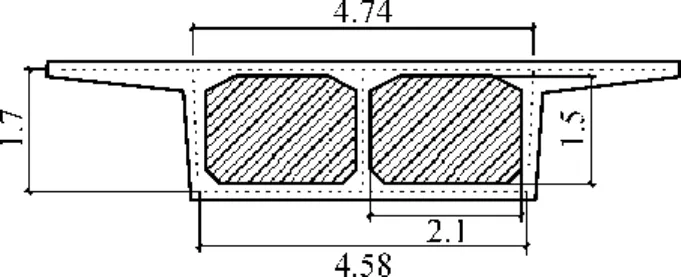
图10 横隔墙尺寸(单位:m)Fig.10 Side wall size(Unit:m)
先选c1=0.4m偏心开孔横隔板,计算其在相对横向位移(箱梁截面顶点相对于底点)时的横向剪切应变能和在相对竖向位移(箱梁截面左侧相对于右侧)时的竖向剪切应变能;为研究横隔板开孔位置对横向剪切应变能的影响,选 3种 c1取不同值的横隔板,比较计算它们在1mm相对横向位移时的横向剪切应变能和单个横隔板的抗剪刚度;最后计算横隔墙在横向位移时的横向剪切应变能.为了验证文中提出的计算方法的正确性,用Ansys有限元软件对每次计算的横隔板或横隔墙进行建模分析,采用SOLID45实体单元来离散,将计算的结果与文中提出的计算方法的结果进行比较.计算结果如图11-15所示.
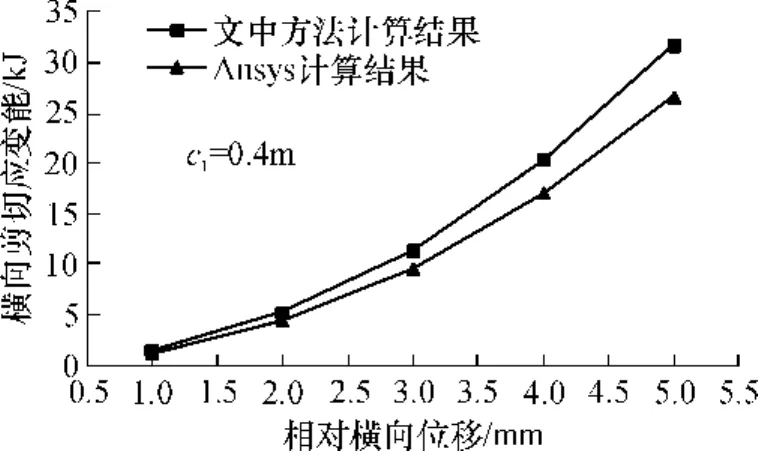
图11 横隔板横向剪切应变能Fig.11 Transverse shear strain energy of diaphragms
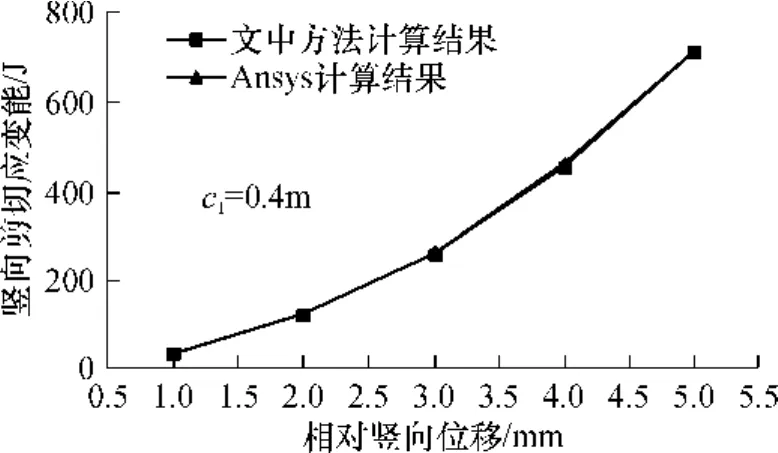
图12 横隔板竖向剪切应变能Fig.12 Vertical shear strain energy of diaphragms

图13 不同c1值横隔板在1mm横向位移时的横向剪切应变能Fig.13 Transverse shear strain energy of diaphragmswith different c1 values under 1mm transverse displacement
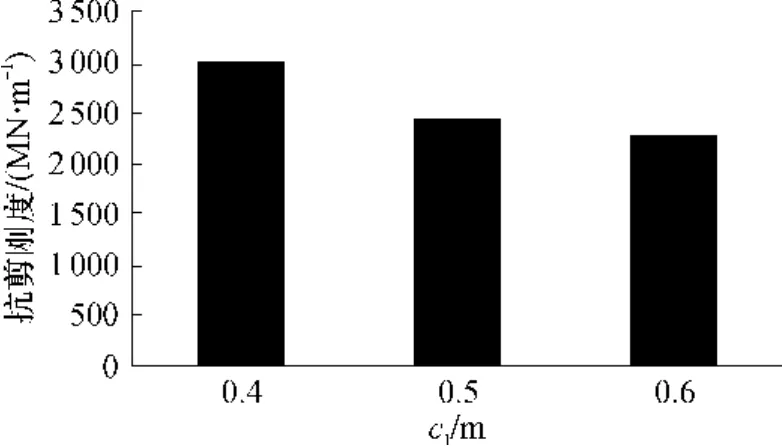
图14 不同c1值单个横隔板在1mm横向位移时的抗剪刚度Fig.14 Shear stiffness of single diaphragm with different c1 values under 1mm transverse disp lacement
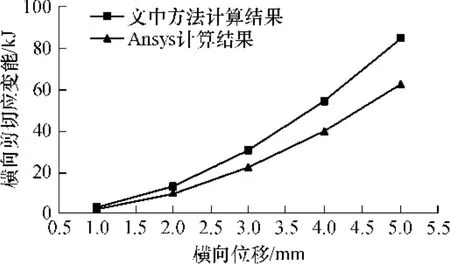
图15 横隔墙横向剪切应变能Fig.15 Transverse shear strain energy of side walls
由图11、12、15可见,文中方法计算结果与Ansys软件计算结果比较接近.
横隔板横向、竖向剪切应变能和横隔墙横向剪切应变能都随位移增加而呈幂函数增加.
在图13中,文中方法与Ansys计算所得的剪切应变能在3种c1取值下都是随c1增大而减少.同时由图13、14可见,c1=0.5c2=0.4m单向偏心开孔横隔板的横向剪切应变能和抗剪刚度在 3种 c1不同取值的横隔板中是最大的.
4.2 文中计算方法与商业有限元软件方法的对比
为保证计算精度,用Ansys有限元软件对c1= 0.4m横隔板进行建模分析时,用了 1 264个 SOLID45实体单元来离散;对c1=0.5m横隔板,用了1332个单元来离散;对c1=0.6m横隔板,用了1216个单元来离散;对梁端横隔墙,用了 1302个单元来离散.在文中提出的计算方法中,对箱梁截面的两个横隔板只是近似视为两个单跨竖立或横卧的具有无穷大刚度横梁的刚架来求其总剪切应变能;对梁端两个横隔墙只是近似视为两个板件来求其横向剪切应变能.而这两种方法计算结果接近.因此,文中计算方法较之商业有限元软件方法更加简便实用.
从文中计算方法的推导可以看出,该方法整个计算思路简洁,物理概念明确,易于推广,适合工程计算需要.
工程实践中,通常要把横隔板、横隔墙纳入整个箱形桥梁或车 -桥系统中去计算,相比于整个桥梁或系统,横隔板、墙的尺寸很小.在商业有限元软件模拟计算中,横隔板、墙只能离散为少数单元,势必减少横隔板、墙的计算精度.而现代箱形梁桥的截面壁薄,承受的荷载大,横隔板、墙抵抗箱梁截面畸变、增加横向刚度的作用越来越重要.横隔板、墙的计算误差过大会大大影响整个箱形桥梁或车 -桥系统的计算精度.而文中计算方法无论是单独计算横隔板或横隔墙还是计算整个箱形桥梁或车-桥系统,对横隔板、墙的计算都不会作任何改变,计算精度保持不变.
采用文中计算方法,可非常容易地把横隔板、横隔墙的刚度组拼到箱梁刚度矩阵车-桥系统刚度矩阵中.
文中是采用钢架柱来计算抗弯刚度,并获得剪切应变能,而钢架柱受长细比的影响.当长细比 = 5.2时,误差为 35.5%,如图15所示;当 =6.4时,误差为19.2%,如图11所示;当 =13.0时,误差为-0.42%,如图12所示.可以看出横隔板开孔越大、箱梁越高,计算误差越小.故文中计算方法适用于大、中跨度预应力箱形梁桥横隔板、墙的剪切应变能计算.
5 结论
文中根据单箱双室箱梁截面的变形设计位移参数,导出横截面横向、竖向畸变角的变位模式;采用刚架或板件来模拟横隔板和横隔墙的计算简图,利用力学和有限元原理推导出横隔板、横隔墙的抗剪刚度、剪切应变能;并将此方法的计算结果与商业有限元软件计算结果进行比较,结果表明:
(1)该方法的计算理论正确可靠,计算结果与商业有限元软件计算结果比较接近;该研究结果为单箱双室梁桥的横隔板和横隔墙提供了一种较完整和可信的研究方法.
(2)该计算方法只用两个具有无穷大刚度横梁的刚架来模拟横隔板、用两个板件来模拟横隔墙,相比于Ansys要用上千个单元来模拟横隔板或横隔墙,该计算方法更加简便实用.
(3)该计算方法对横隔板、横隔墙无论是单独计算还是置入整个箱形桥梁或车 -桥系统中计算,计算精度都保持不变.
(4)该计算方法思路简洁,物理概念明确,易于推广,可非常容易地把横隔板、横隔墙的刚度组拼到箱梁刚度矩阵车-桥系统刚度矩阵中.
(5)该计算方法可以计算任意单向偏心开孔横隔板的横向剪切应变能.计算结果表明,靠近中腹板部分的横隔板宽度 c1为靠近边腹板部分的横隔板宽度 c2的一半时的横隔板是单箱双室箱梁横隔板开孔位置的最佳选择.
(6)该计算方法适用于大、中跨度预应力箱形梁桥横隔板、墙的剪切应变能计算.
(7)横隔板横向、竖向剪切应变能和横隔墙横向剪切应变能都随位移增加而呈幂函数增加,这说明横隔板和横隔墙对增加箱梁截面的横向刚度,抵抗截面畸变的作用很大,它们的严格设置和研究对现代箱形桥梁建设尤为重要.
[1] Ashebo D B,Chan T H T,Yu L.Evaluation of dynamic loads on a skew box girder continuous bridge(part I): field test andmodal analysis[J].Engineering Structures, 2007,29:1052-1063.
[2] Zhang J,Huo Y.Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method[J].Engineering Structures,2009, 31:1648-1660.
[3] 伊航,刘保东,任红伟.波纹钢腹板混泥土箱梁的动力特性分析 [J].工程抗震与加固改造,2008,30(2): 29-32.
Yi Hang,Liu Bao-dong,Ren Hong-wei.Analysis of the dynamic characteristic of concrete box-girders with corrugated steel webs[J].Earthquake Resistant Engineering and Retrofitting,2008,30(2):29-32.
[4] Moon J,Yi J,Choi B H,et al.Lateral-torsional bucklingof I-girder with corrugated webs underuniform bending[J]. Thin-Walled Structures,2009,47:21-30.
[5] 刘小渝,孙童龄.横隔板对钢箱梁受力畸变的分析[J].重庆交通大学学报:自然科学版,2007,26(5):9-12.
Liu Xiao-yu,Sun Tong-ling.Effectof diaphragm on distortion of steel box girder[J].Journal of Chongqing Jiaotong University:Natural Science,2007,26(5):9-12.
[6] 连军,贾磊,郝宪武,等.横隔板设置对薄壁钢箱梁畸变效应影响研究 [J].交通标准化,2007(11):202-207.
Lian Jun,Jia Lei,Hao Xian-wu,et al.The influence of transverse diaphragm design on the distortion of thin-wall steel box girder[J].Communications Standardization, 2007(11):202-207.
[7] 曾庆元,郭向荣.列车桥梁时变系统振动分析理论与应用[M].北京:中国铁道出版社,1999.
[8] 王荣辉.杆板壳结构计算理论及应用 [M].北京:中国铁道出版社,1999.
[9] Kim K,Yoo CH.Bending behaviors of quasi-closed trapezoidal box girderswith X-type internal cross-frames[J]. Journal of Constructional Steel Research,2009,65:1827-1835.

