求解混流装配线调度的疫苗共生克隆选择算法*

刘冉 楼佩煌 唐敦兵 杨雷

(1.南京航空航天大学机电学院,江苏南京 210016;2.江苏天奇物流系统工程股份有限公司,江苏无锡 214187)

在实际应用中,混流装配线(MMAL)经常需要同时考虑几种互相存在冲突的目标函数.因此,混流装配线调度优化问题的理论研究逐渐从单目标优化问题转变为多目标优化问题.部分学者采用目标权重法解决混流装配线的多目标调度优化问题,如Bard等[1]考虑了最小化生产线长度和平顺化零件消耗率两个优化目标,并用禁忌搜索对加权后的目标函数求解,Tavakkoli-Moghaddam等[2]加权处理了最小化总公共作业时间成本,平顺化生产率,最小化设备更换成本3个目标函数,并用Memetic算法解决了两种规模的调度优化问题.但是,用加权目标函数法解决多目标优化问题需要依赖先验知识确定权重系数,且只能找到解空间的部分解,有一定的局限性.为弥补这个缺陷,基于Pareto最优的多目标优化算法得到了广泛应用.比较有代表性的有:Hyun等[3]提出了层次小生境遗传算法,用于解决最小化总效用时间等 3个目标函数的排序问题,基于小生境的选择机制可以维持解的多样性,从而得到更均匀的Pareto前端;McMullen等[4]用多目标遗传算法,研究了以最小化设备更换成本和平顺化零件使用率为目标函数的排序问题;Mansouri[5]结合非支配搜索策略和小生境选择机制,提出一种遗传算法重新研究了McMullen的问题模型;苏平等[6]提出改进的遗传模拟退火算法同时优化了最小生产循环周期和零部件消耗率两个目标函数.该算法借助模拟退火算法对适应度尺度进行调整,以改善遗传算法的早熟收敛问题.

以上分析可以看出,多目标遗传算法作为解决混流调度问题的主要方法得以广泛研究.但是遗传算法一直存在早熟收敛这个缺陷,多目标优化算法最后要得到一个多样解群体,这个缺陷会严重影响算法的结果质量.尽管针对这个缺陷的各种改善方法被大量提出,但是其本身依然有局限性,即采用小生境选择机制的遗传算法[3,5],其结果的优劣过于依赖小生境参数的选取,遗传模拟退火算法对适应度差异的拉伸会导致潜在最优解的丢失等[6].通过借鉴自然免疫系统而得到的克隆选择算法,因为其自身高频变异及抗体评价的特性,可以抑制相似解的大量繁殖,能有效避开遗传算法的早熟收敛问题[7],更适于多目标优化问题的求解.文中针对多目标的混流装配线调度优化问题,提出一种疫苗协同进化的免疫克隆选择多目标优化算法(MO-VECSA).此算法不仅有抗体群,还设计了疫苗种群,并定义了相关进化操作;针对目标函数之间存在冲突的问题,采取从最优个体中提取疫苗,进化后又去注射给抗体群,以提高抗体群质量;针对待求问题的离散性,改进了克隆选择算法中抗体亲和度的评价方式.最后,通过两组不同的数值仿真实验,验证了文中提出算法的有效性.

1 多目标混流装配线调度模型

在一个计划周期内,混流装配线上共装配M种产品,第m种产品的需求量为Dm,则M种产品总需求量为在实际生产中,采用MPS (Minimum Part Set)法.如果M种产品总需求量的最大公约数为h,MPS为一向量集(d1,…,dm)=(D1/.在调度过程中,只对位产品进行排序,重复 h次,即可得到所有产品的投产顺序.

文中选择最小化零部件消耗率及最小化设备更换成本这两个较为常见的目标进行优化.这两个标准在很多文献中都作为混流装配线排程优化的目标函数[2,5,8].表达式如下:

(1)最小化零部件消耗率

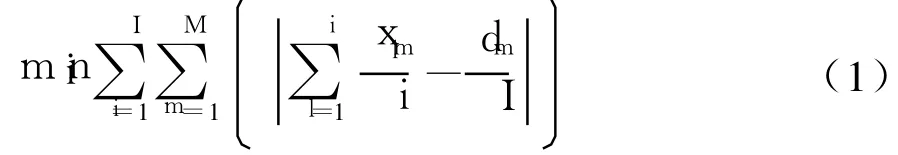
如果序列中第1个产品是m型,二元决策变量xlm值为 1,其它情况为 0.式中第 1项为到第 i个已装配的产品为止,m型产品出现的比率;第2项为m型产品的数量占所有产品的比率,也即期望生产率.

(2)最小化生产准备成本

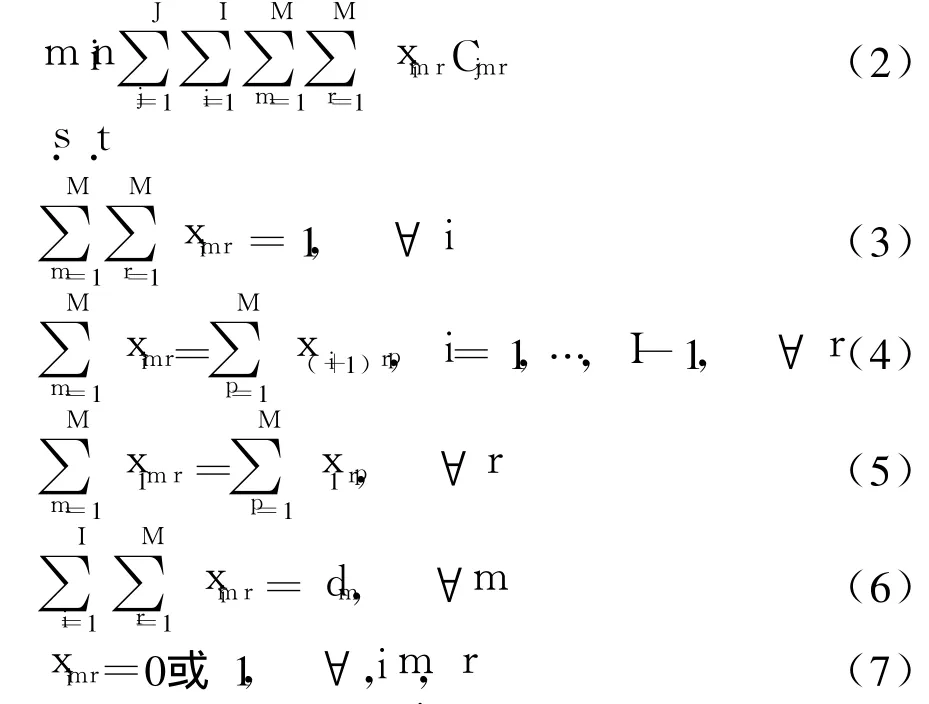
式中:Cjmr为在工作区间j生产m型产品转换成r型产品所消耗的生产成本;J为工作区间总数.在一个生产序列中,当第i位产品模型为m而i+1位为r时,二元决策变量 ximr为 1,其余情况则为 0.

2 MO-VECSA的算法设计

在人工免疫系统中,对于某特定抗体 a,给其接种疫苗是指按照先验知识来修改 a的某些基因位上的基因或者分量,使得此抗体以较大的概率具有更高的适应度[7].某些情况下,针对待求问题很难获得较为准确的先验知识,例如文中列举目标模型,从直观上分析,如果想降低设备更换成本,那么同种模型的生产应该越密集越好,但是这样的生产模式势必引起出产率的不均匀,从而影响零部件消耗率的平顺化.因此,文中采取另一种方式,从最佳个体基因中提取疫苗.MO-VECSA算法的具体设计如下.

2.1 抗体和疫苗的编码

2.1.1 抗体编码

针对混流调度这一特定问题,采用产品的投产顺序直接编码,每个基因位对应一个产品的品种,如最小生产循环(d1,d2,d3)=(5,3,2)的一种排序方式的抗体编码为:“AABBBCCAAA”.

2.1.2 疫苗编码

文中依据目标函数的特点,设计随机抽取最佳抗体的基因片段生成疫苗,如图 1所示.“*”为通配符,仅为记录疫苗片断在主抗体中的位置而设计,不参加任何操作.

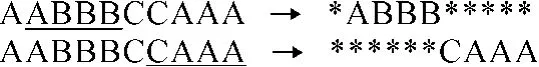
图1 疫苗的生成Fig.1 Generation of vaccine

2.2 产生初始种群

因为算法开始时并没有优良抗体提供必要信息,这里定义初始疫苗种群为一空的集合,即 V0←,疫苗种群的大小取为抗体群大小的 10%.抗体群A0则随机生成.

2.3 抗体种群的进化

2.3.1 抗体的评价并生成自适应克隆算子

免疫算法中,克隆比率一般取为抗体的抗体亲和度和抗原亲和度的函数.抗体亲和度衡量抗体之间的相似程度,抗原亲和度度量解与目标的匹配程度.标准的克隆免疫算法只把抗体编码的相似程度作为抗体亲和度的评价参数[8],而混流装配线调度问题的决策变量和目标函数之间并不是一一映射的关系,即不同的编码方式可能产生相同的目标函数值,单从抗体的基因型来评价是不够的,还需要考虑目标函数值的影响.因此文中算法提出把抗体的基因型(编码)和表现型(目标函数)同时作为抗体亲和度的参数.

抗体解码后,可以将抗体群基于非支配分级[9],第一级的抗体集即为全种群的非支配集.设抗体群依据目标函数的非支配关系,共被分为 R个质量等级.ai和aj同为质量级r内的两个抗体.r值越小,抗体质量越高,则抗体与抗原匹配程度越高.抗体ai抗原亲和度ξai设计为

基因型亲和力定义为

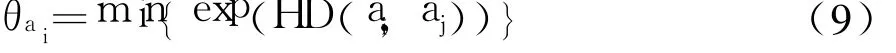
式中:HD(ai,aj)为ai和aj的海明距离.

表现型亲和力设计为

式中:dai为抗体ai的拥挤距离[9].dmax为ai所在质量级所有抗体的拥挤距离最大值.抗体的拥挤距离小,说明其与相邻抗体的目标函数取值接近,这样不利于得到分布均匀的pareto前端,应该抑制其大量繁殖.

综上所述,ai的自适应克隆算子Cai为

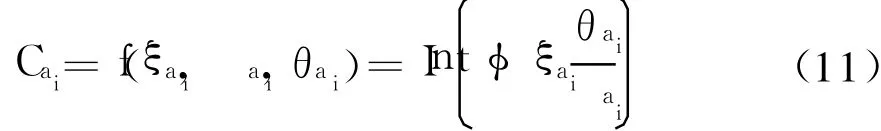
式中:Int(◦)为上取整函数;φ为与克隆规模有关的可调系数.

2.3.2 抗体的变异

抗体自适应变异率εt设计如下:

式中:δ为衰退因子;ε0为初始变异率;t为进化代数; ri为质量级数.这种动态的选取可在进化早期维持较高的变异率,而在后期种群趋于成熟时减小扰动,有利于算法的收敛.这种变异率还赋予质量等级较低的抗体更高的活性,增大其转化为优秀抗体的几率.

2.3.3 产生新抗体群

抗体群At经过克隆,变异操作后,种群空间得以扩张.由于变异后子代个体质量参差不齐,有必要淘汰劣质个体,以维持种群大小的衡定.算法采取按照质量等级依次对每层的抗体进行局部非支配分级并保存每层抗体的非支配解集,以生成新抗体群 At+1.算法在每次迭代过程中都采取这种局部寻优操作,加快了算法的收敛速度,同时又考虑到非最优解集中的优秀个体并将其保留至新抗体群,增强了种群的多样性,防止算法早熟收敛.

2.4 疫苗种群的进化

2.4.1 疫苗注射

疫苗注射操作如图 2所示.对抗体 ai和疫苗vi,注射疫苗定义为,将vi的基因替换 ai中相应位置的基因片断,并修改 ai其余部分的基因,使其满足最小生产循环的比率;如果注射后的抗体a′i支配ai,则a′i取代ai.

图2 疫苗注射操作Fig.2 Operator of vaccination

2.4.2 疫苗评价与更新

设疫苗vi有Γvi次注射机会,注射后有个新抗体支配并替代了老抗体,则疫苗vi的适应度值定义如下:

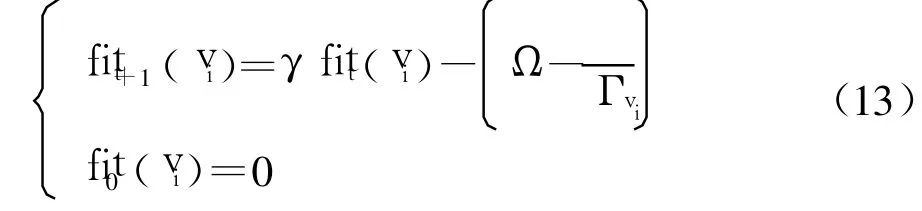
式中:γ为小于 1的衰退系数;Ω为疫苗注射成功率的期望阈值.进化过程中,适应度低于 0的疫苗将被淘汰.新疫苗则在抗体群非支配集的不同个体中随机抽取.在算法运行过程中,每经历一定代数,适应度值最高的疫苗有进化的机会,在此定义为注射次数的增加,即Γi=Γi+1.

2.5 MO-VECSA算法流程

图3是MO-VECSA的算法流程,实线箭头表示种群自身的进化过程,而虚线箭头表示种群之间信息的传递.疫苗种群从抗体种群中获得最优解的部分基因信息,经过自身评价并进化后又去注射给抗体种群,以提高抗体种群的整体质量.两者相互影响又独立成长,最终实现协同进化.

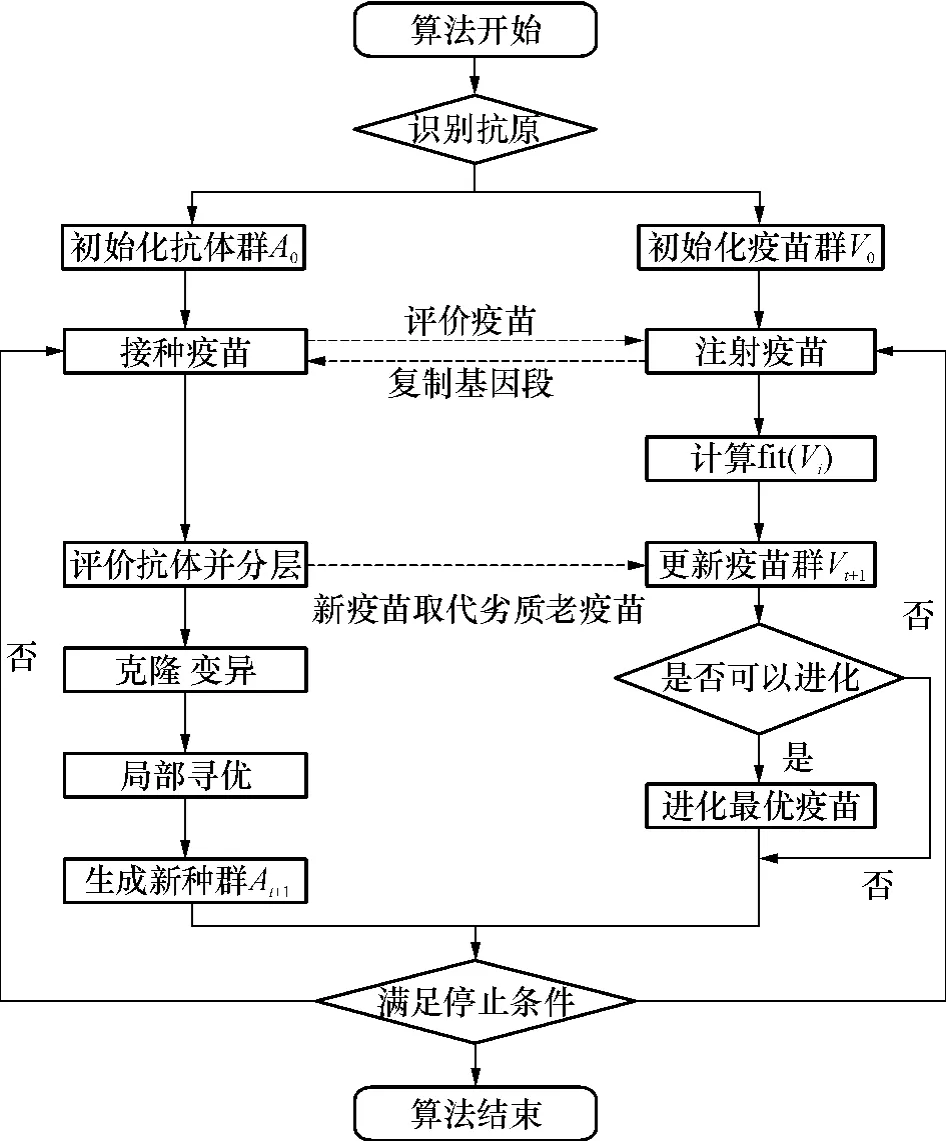
图3 MO-VECSA流程图Fig.3 Flowchart of MO-VECSA

3 实例仿真与算法比较分析

3.1 疫苗种群对克隆选择算法的影响

为了对疫苗种群对算法的影响进行分析,文中设计了只有一个抗体群的克隆选择算法(MOCSA)并与之进行比较.MOCSA没有接种疫苗的操作,其余进化过程则与MO-VECSA类似.

某企业一混流装配线生产3种产品,MPS比例为 6∶2∶2.为计算方便,假设生产成本只发生在第一工作区间,具体数值见表1.Pareto最优解集见表2. MO-VECSA抗体种群大小为50,迭代次数为50,ε0= 0.1,δ=0.02,γ=0.8,Ω=0.5.MOCSA种群大小、迭代次数、变异率等均与MO-VECSA相同.

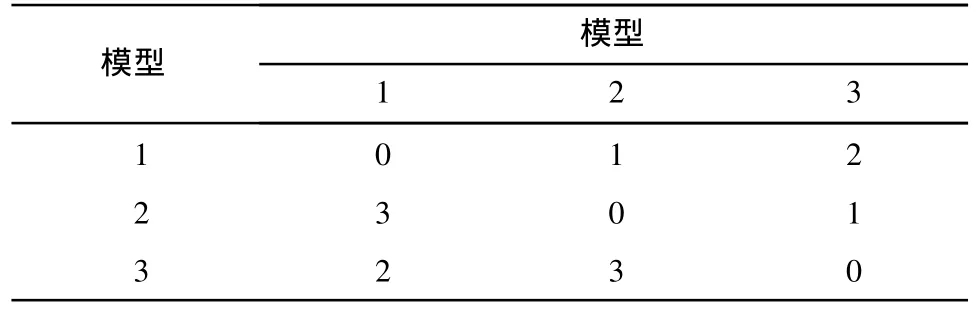
表1 设备更换成本Table 1 Setup costof differentmodels

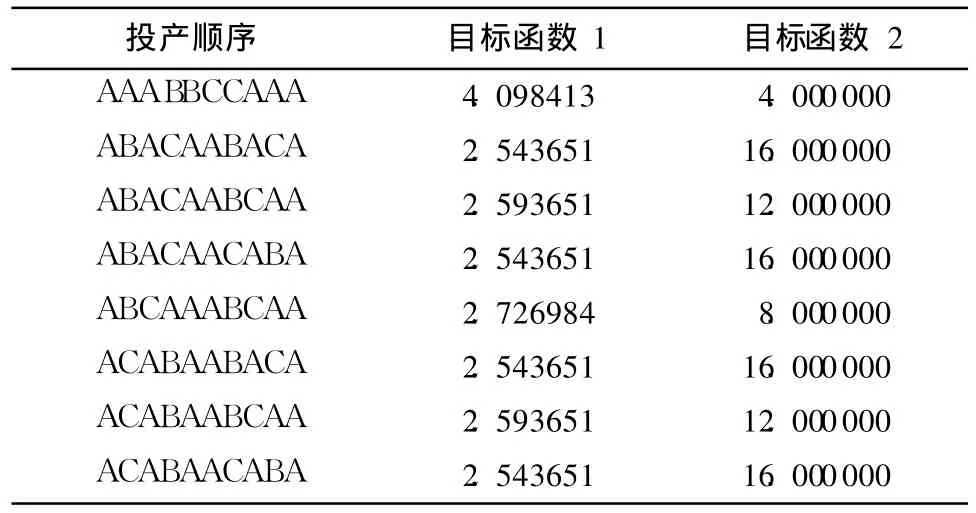
表2 Pareto最优解Table 2 Pareto optimal solutions

图4为两种算法均运行 20次,得到的近似最优解集中所含个体数的比较.图 5为所得解集中属于Pareto最优解的个数的比较.从图4和5中可以看出无论是在解集数量还是在解集质量上,MO-VECSA所得的算法结果均优于MOCSA,且MO-VECSA所得结果更稳定.图 6为两算法迭代 20次结果的平均值,可以直观地看出,采用了疫苗种群协同进化的克隆选择算法的确可以得到更好的结果.

图4 所得解集的大小Fig.4 Size of the solution set

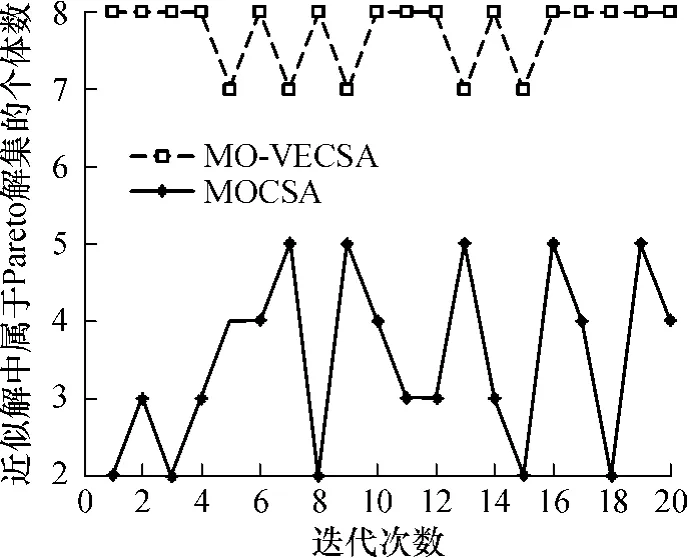
图5 Pareto最优解的个数Fig.5 Number of Pareto solutions

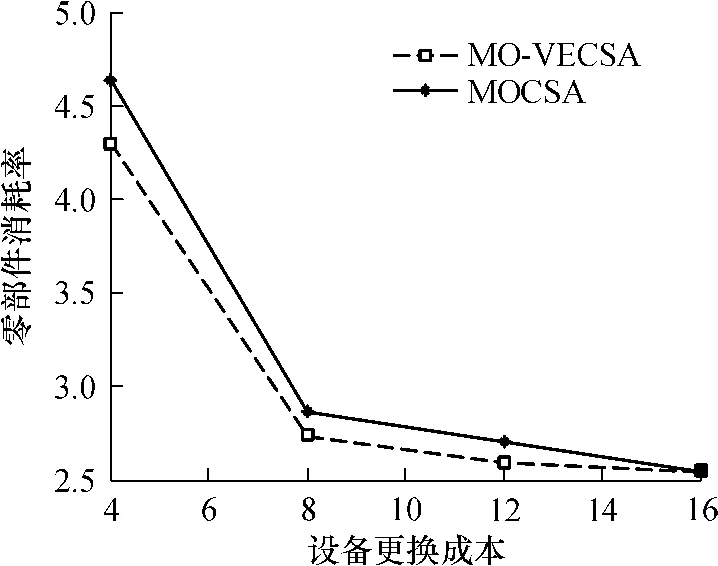
图6 平均结果值的比较Fig.6 Comparison of the average results

3.2 MO-VECSA算法整体性能评价

为了全面评价MO-VECSA的整体性能,文中采用CSMOA[10]、NSGA-II[9]、SPEA2作为比较算法[11].NSGA-II和SPEA2是两种经典的多目标遗传算法,CSMOA是一种只有抗体种群进化的多目标免疫克隆选择算法.因为仿真实例规模较大,无法得到Pareto最优解集,文中从常用的几种多目标优化算法的评价准则中选择前端范围FS(S)和覆盖评价函数˜C作为评价函数.

(1)前端范围:

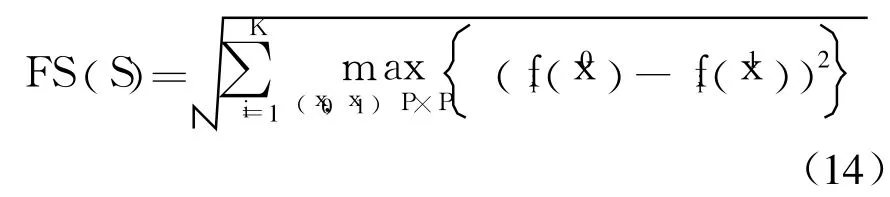
式中:S为非支配解集P在目标空间的像;K为目标函数的个数;fi(x0)、fi(x1)分别为解x0和x1的目标函数值.FS(S)用来测量近似集覆盖目标空间的大小.前端范围的值越大,解的多样性越好.

(2)覆盖评价函数:

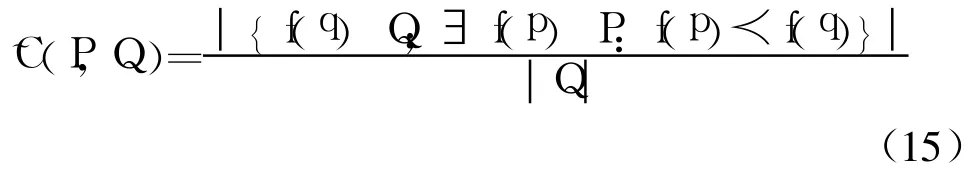
式中:˜C测度计算了解集Q中被P占优的解的比例;p、q为P、Q解集中的解个体.

某企业一汽车总装线共组装5种车型,MPS比例为 3∶4∶6∶6∶1.为计算简便,假设设备更换成本均发生在第一工作站,且值为1.MO-VECSA抗体种群大小取 500,疫苗种群为 50,迭代次数为 100.其余算法的参数均取与MO-VECSA相当的数值.所有算法均运算 30次,对两个评价准则取平均值,见图 7和表 3.

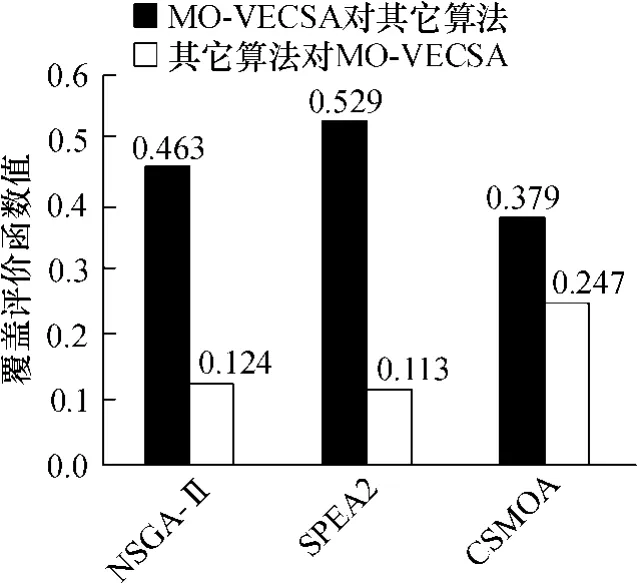
图7 覆盖评价函数柱形图Fig.7 Histogram of the function coverage evaluation

表3 前端范围平均结果比较Table 3 Comparison of FS(S)

图7表明,MO-VECSA的近似集支配NSGA-II和SPEA 2得到大量非劣解,解集覆盖均在50%左右,对CSMOA也有近40%的支配率.而NSGA-II和SPEA 2只支配MO-VECSA的非劣面的很小一部分,均低于20%,CSMOA略高.这说明MO-VECSA得到的近似Pareto解集的质量要高于其余几种算法.表3中数据表明,对于前端范围评价函数,MO-VECSA也优于其余3种算法,这证明了MO-VECSA可以得到分布范围更广阔的近似最优解集.

图8是几种算法得到的平均结果比较图,从图中可以看出,MO-VECSA曲线最低,算法结果略优于CSMOA,对NSGA-II和SPEA2则有了较大改进.

图8 四种算法平均结果比较Fig.8 Comparison of the average results of the four algorithms

4 结语

文中针对混流装配线调度优化问题的平顺化零件使用率和最小化设备更换成本两个优化目标,提出一种疫苗协同进化的多目标免疫克隆选择算法.通过对两组实例仿真以全面测度算法的性能.第一组仿真通过易于得到Pareto前端的小规模实例证明了文中算法提出的疫苗种群对免疫克隆选择算法性能的改善,得到的近似最优集无论是在解集数量还是质量上都比单抗体种群进化的算法有所提高.第二组仿真选择了NSGA-II、SPEA 2、CSMOA 3种算法作为比较算法,算法结果证明了文中提出的算法可以得到非支配占优比例更高,且分布更广阔的Pareto近似解集,更适于大规模混流装配线调度优化的求解.

[1] Bard J F,Shtub A,Joshi S B.Sequencing m ixed-model assembly lines to level parts usage and m inimize line length[J].Int JProd Res,1994,32(1):2431-2454.

[2] Tavakkoli-Moghaddam R,Rahimi-Vahed A R.Multi-criteria sequencing prob lem for am ixed-model assemb ly line in a JIT production system[J].Applied Mathematics and Computation,2006,181(2):1471-1481.

[3] Hyun C J,Kim Y,Kim Y K.A genetic algorithm formultiple objective sequencing problems in mixed model assembly lines[J].Comput Oper Res,1998,25(7/8):675-690.

[4] McMullen P R.An efficient frontier approach to addressing JIT sequencing problemswith setups via search heuristics[J].Comput Ind Eng,2001,41(3):335-353.

[5] Mansouri S A.A multi-objective genetic algorithm for mixed-model sequencing on JIT assembly lines[J].Eur J Oper Res,2005,167(3):696-716.

[6] 苏平,于兆勤.基于混合遗传算法的混合装配线排序问题研究 [J].计算机集成制造系统,2008,14(5): 1001-1007.

Su Ping,Yu Zhao-qiu.Hybrid genetic algorithms for sequencing problems in mixed model assemb ly lines[J]. Computer Integrated Manufacturing Systems,2008,14(5): 1001-1007.

[7] 焦李成,杜海峰,刘芳,等.免疫优化计算,学习与识别[M].北京:科学出版社,2006.

[8] Rahimi-Vahed A,Mirzaei A H.A hybrid mu lti-objective shuffled frog-leaping algorithm for am ixed-model assembly line sequencing problem[J].Computers＆Industrial Engineering,2007,53(4):642-666.

[9] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transaction on evolutionary Computation,2002,6(2):182-197.

[10] 尚荣华,马文萍,焦李成,等.用于求解多目标优化问题的克隆选择算法 [J].西安电子科技大学学报, 2007,34(5):716-721.

Shang Rong-hua,Ma Wen-ping,Jiao Li-cheng,et al.Conal selection algorithm for multi-ob jective optimization problems[J].Journal of Xidian University,2007,34 (5):716-721.

[11] Zitzler E,Laumanns M,Thiele L.SPEA2:Imp roving the strength pareto evolutionary algorithm for mu ltiobjective optim ization[C]∥Proceedings of the Third Conference on Evolutionary and Determ inistic Methods for Design, Optim ization and Control with App lications to Industrial and Societal Problems(EUROGEN 2001).Athens:[s. n.],2002:95-100.