压电换能器锁相环频率跟踪的失效分析与解决

武剑 董惠娟 张广玉

(哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)

碳纤维复合材料的比强度高、比模量大,在航空宇航制造工程领域获得了广泛应用.但该种材料的硬度高(HRC60左右)而层间剪切强度较低(＜100 MPa),传统钻孔加工时经常出现出入口劈裂、中间分层掉渣和刀具磨损等不良现象.有关研究表明,以功率超声为基础的超声振动钻孔技术可有效解决这一问题,加工质量可提高且缩短加工周期[1].换能器作为功率超声技术的核心部件,在加工过程中应处于机械谐振状态,因此可靠的频率跟踪技术就成了保证碳纤维复合材料振动钻孔质量的关键因素.

目前采用的频率跟踪方式主要有最大电流搜索式[2]、最大功率搜索式[3]、最大导纳跟踪式和锁相环(PLL)式等[4-5].其中前三者的共同缺点是需要超声电源具有主动扫频功能,在换能器机械谐振频率变化剧烈的场合,频繁的扫频将使换能器工作于谐振频率的时间比例减小,效率降低.而PLL频率跟踪技术电路结构简单,无需主动扫频,可使超声电源振荡频率自动动态保持在换能器机械谐振频率处,故获得了广泛应用[6].其原理是当超声电源振荡频率高于换能器机械谐振频率 ωs时,换能器两端电压与通过其电流的相差为正,反之为负,据此不断调节超声电源频率使相差保持为零而实现跟踪[7].

换能器在其理想跟踪点ωs附近存在两个距离较近的相位零点 ω1和 ω2,其中 ω1较低且接近于ωs,故为PLL的目标跟踪点.PLL依赖于相位零点但无法区分 ω1和 ω2,故可能发生误跟踪,须将跟踪范围设定在 ω1附近以避免之.但当 ωs的变化超出此范围时,会导致 PLL死锁于设定频段的顶端[6].文中分析指出:当换能器重载(动态电阻变大)或其静态电容较大时,不但 ω1与ω2间距减小,更易发生误跟踪和死锁,而且 ωs与 ω1间距增大,换能器相位曲线趋于平缓,直至相位零点消失,使PLL跟踪误差增大甚至失锁.故较大的动态电阻和静态电容是导致PLL跟踪失效的重要原因,制约了PLL跟踪技术的进一步应用.在研究动态电阻和静态电容导致跟踪失效作用规律的基础上,文中指出抵消静态电容的影响是解决该问题的必由之路,并提出一种静态电容补偿法,可使换能器相位零点的数量由两个变为一个(且必有一个),该点对应于ωs,有效解决了跟踪失效问题.

1 PLL频率跟踪4种失效形式的分析

图1所示为压电换能器在其机械谐振频率附近的等效电路[8].

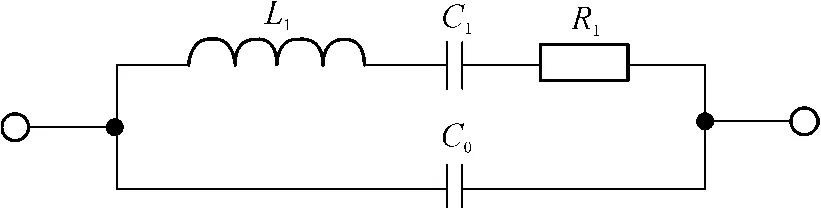
图1 压电换能器等效电路Fig.1 Equivalent circuitof a piezoelectric transducer

图1中,L1为动态电感,C1为动态电容,R1为动态电阻(分别表征换能器的质量、机械顺和机械内阻),三者构成等效电路的机械臂支路;C0为静态电容,是电学臂支路.Yoko Mizutani等[9]给出了换能器阻抗Z、相位θ与角频率ω的函数关系:

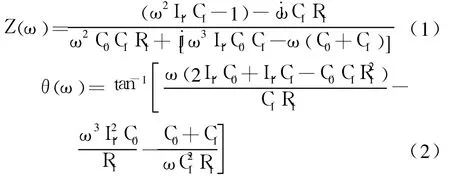
基于式(1)和(2),详细分析目前PLL频率跟踪技术存在的主要问题.

1.1 失锁

采用PLL方式对换能器进行频率跟踪,必然要求换能器相位曲线(函数式(2))与横轴有交点,否则将导致跟踪失效形式之一的失锁.令θ(ω)=0,得到:

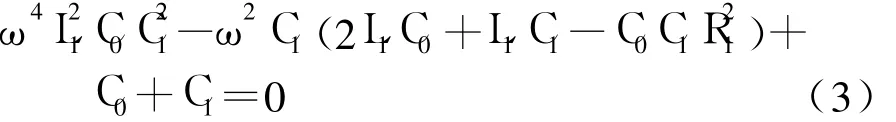
式(3)为关于ω2的一元二次方程,为使相位曲线与横轴有交点,须有判别式Δ≥0,即:

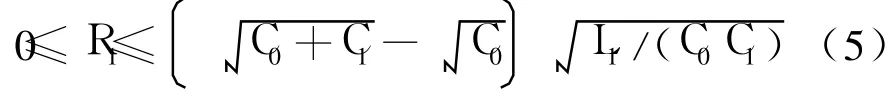
或者

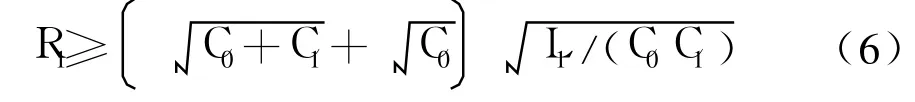
实际中C0≫C1,故式(6)下限为据此计算出的换能器机械质因数Qm仅为

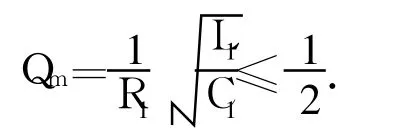
实际中Qm值为数百至数千,式(6)意味着换能器机械内阻过高,故舍去.

换角度分析,式(4)也可化为关于C0的一元二次不等式,即:

解之得到:

若L1和C1不变,为确保方程(3)有解,R1和C0须满足式(5)和(8)所构成的约束范围,否则将导致PLL失锁.值得注意的是,通过使C0趋近于0,可使式(5)的上限趋于无穷大,则方程(3)一定有解,必然不会失锁.

1.2 误跟踪与死锁

以下讨论在 Δ＞0的条件下进行.考虑到 ω＞0,解方程(3),得到:

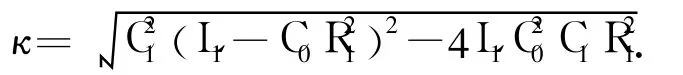
方程(3)有两个根,本应锁定在ω1的PLL有可能错误地锁定到 ω2,从而导致第二种跟踪失效,即误跟踪.

为避免误跟踪,须将PLL跟踪频率限定在以换能器空载时 ω1为中心、宽度为 Δω=ω2-ω1的范围内,使其不会跟踪到 ω2.但若由于负载的剧烈变化而使 ωs超出此范围的话,将造成第三种跟踪失效——PLL死锁于Δω的上限.

显然当 ω1和 ω2距离较近时更容易发生误跟踪.为考查二者间距,做如下运算:

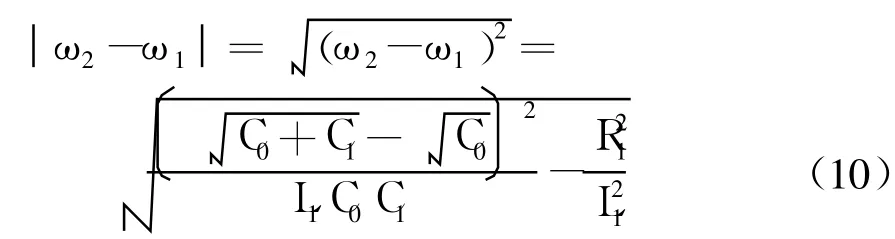
式 (10)中,若L1和C1不变,C0和R1越大,ω1和ω2间距越小,PLL也就越容易发生误跟踪和死锁;但如果 C0较小,则即使在 R1较大的情况下 ω1和 ω2仍然保持较大间距.值得注意的是,通过使 C0趋于 0,可使 ω1和 ω2的间距为无穷大,即消除了误跟踪的可能性,从而也就无需限定跟踪范围,避免了死锁问题.

1.3 跟踪误差大

ω1为PLL跟踪的目标频率,而换能器机械谐振频率为

超声电源的振荡频率应为 ωs,以保持换能器的机械谐振状态.为考查PLL的跟踪准确度,即ω1与ωs的间距,做如下运算:

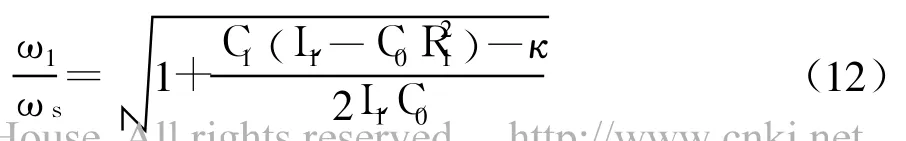
某实际换能器L1=50.02mH,C1=279.1pF,对一系列C0,按式(5)计算R1的可取范围,以式(12)考查两者变化对 ω1与 ωs间距的影响,结果如图 2所示.

图2 R1和C0对PLL跟踪准确度的影响Fig.2 Influences of R1 and C1 on PLL tracking accuracy

结果表明,在约束范围内,R1和 C0越大,ω1与ωs间距越大,跟踪精度也就越低;对于同样的R1,C0越小跟踪精度越高.特别地,可证:

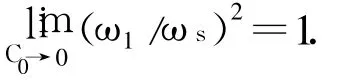
即通过使C0趋于0,可使PLL跟踪误差消失.

综上所述,较大的R1和C0将导致PLL失锁、误跟踪、死锁和跟踪误差大 4种跟踪失效,但总可以通过使C0趋于0来解决.据式(8)、(10)和(12),虽然使 R1趋于 0也可避免失锁和跟踪误差大的问题,并降低误跟踪和死锁的可能性,但 R1由换能器的材料、装配工艺和载荷决定,且在实际过程中不断变化,难以使之为零,故设法抵消 C0就成了解决上述跟踪失效问题的必由之路.在换能器回路上接入匹配电感是抵消C0的常用方法,但此法只能在某个频点(一般设计为空载时的 ωs)起作用[10],适应能力较差.

由此,若能在宽频带内准确抵消静态电容 C0,达到使 PLL能准确跟踪 ωs变化之目的,将是十分必要且有意义的,此方法即“静态电容补偿法”.

2 静态电容补偿法

由式(11)知,ωs取决于机械臂支路,而与电学臂支路无关.设换能器端电压为u(t),机械臂支路电流为i1(t),电学臂支路电流为i0(t).若能测量u(t)和i1(t)的相差θ1(ω),根据LCR串联谐振回路性质,θ1(ω)为正,则说明激励频率高于ωs,反之说明频率偏低,通过调节超声电源频率使 θ1(ω)保持为0,则可实现准确频率跟踪.u(t)可测,但机械臂支路和电学臂支路在物理上不可分,故i1(t)不可独立测量,而只能测量换能器总电流i(t).根据等效电路可知,i(t)的表达式为

C0是真实电容,故i0(t)可根据下式计算:

由此可计算出i1(t):

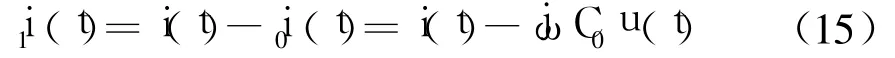
式(15)说明,只要能实时测量超声电源的角频率ω,并事先准确测量 C0,就可以按照式(15)从i(t)中除去i0(t),补偿C0的分流作用,得到i1(t),继而便能得到任意频率下的θ1(ω),将其作为PLL跟踪的依据,即可实现在任意宽频带内 C0的补偿,使换能器对PLL呈现出其机械臂支路(即LCR串联谐振回路)特性,解决跟踪失效问题.

式(15)存在复数运算,当激励电压为正弦时可进一步简化.设:

式中:Umax为u(t)的峰值,φ为初相.

根据电容的伏安特性,可得到i0(t):

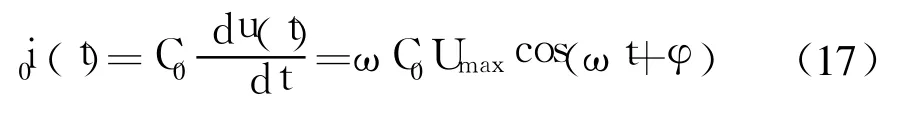
将式(17)带入式(15),得到正弦激励下i1(t)的表达式:

式(18)所描述的算法既可用模拟电路实现,也可由以单片机或DSP为核心的数字系统实现.前者实时性良好,但电路调整复杂并易受干扰,因此选用数字系统实现,以下给出一个实用方案及其实验结果.

3 跟踪系统数字化实现方案与实验验证

3.1 系统构成

文中设计并实现的数字化频率跟踪系统的结构图如图3所示.图中,ADC为模数转换器,DAC为数换转换器.

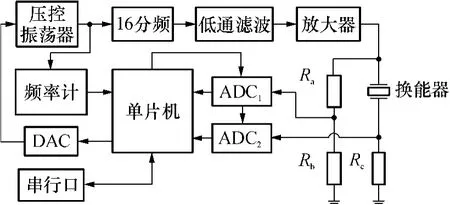
图3 基于静态电容补偿的数字化频率跟踪系统结构图Fig.3 Digital frequency tracking system's diagram based on static capacitance com pensation

系统首先通过频率计测量当前压控振荡器(VCO)振荡频率,经过16分频后得到换能器的激励频率ω;ADC1和ADC2分别采集换能器两端电压和通过电流(为避免引入额外相位差,由单片机控制两者同时采样,采样周期为Tsample),获得序列u(n)和i(n).

将式(18)离散化,得:

式中:n=0,1,2,….

式(19)用于计算i1(n).又因换能器机械臂支路仅由电感、电容和电阻元件构成,故 i1(n)为与u(n)同频率的正弦序列,设其表达式为

从而机械臂相位差θ1(ω)可表示为

式中:φ、φ1均可由线性拟合法测得[11].根据 θ1(ω)控制DAC输出电压,调节VCO振荡频率,同时也就调节了换能器的激励频率,实现闭环控制.这里采用 16分频器的目的是使系统可在较短时间内(1/16s)得到当前换能器激励频率的准确值(精确至±1Hz),以提高跟踪速度和计算精度;串行口用于和上位PC通信.

3.2 实验验证

按第 2节所述原理和图 3所示结构研制的超声电源样机与其它实验设备的实物照片如图 4(a)所示.为验证文中所述理论的正确性及跟踪系统的性能,一并设计了如图4(b)所示的实验系统,其中换能器与负载质量块之间的橡胶垫用于增强稳定性.

实验换能器标称频率为 20kHz,经阻抗分析仪测量,其静态电容为11.0488nF.

实验过程描述如下:设定阻抗分析仪的扫频范围为17～23kHz(通常超声振动加工时换能器的机械谐振频率偏移不会超出±3 kHz),并在整个实验过程中保持不变;超声电源工作电压保持为80V,关闭其自动跟踪功能.①切换开关,使换能器与阻抗分析仪相连接,并用适当质量的砝码给换能器加载.②在设定的扫频范围内,用阻抗分析仪对加载的换能器进行相位测量,得到换能器的整体相位曲线,而后用分析仪的导纳圆功能测得当前负载下的ωs.③保持换能器负载不变,切换开关,使换能器与超声电源相连,在上述扫频范围内,手动调节电源振荡频率,并通过串行口向上位PC机发送该频率下θ1(ω)的测量结果.④保存数据,回到第①步,换用不同质量的砝码,重复实验.

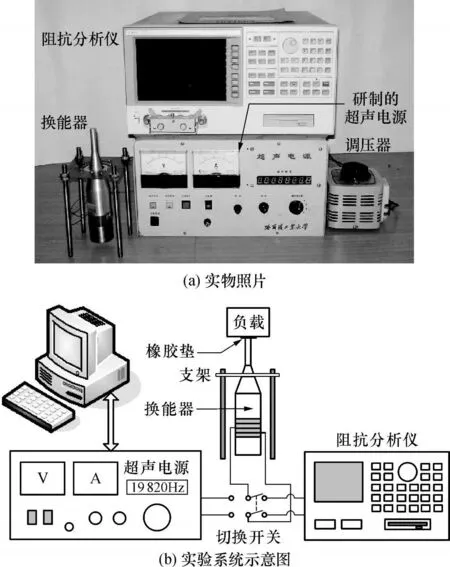
图4 实物照片与实验系统示意图Fig.4 Picture and diagram of experiment system

实验完毕,将超声电源测得的数据绘制成图,观察其是否与LCR串联谐振回路特性相符:①相位曲线与横轴必有交点(无失锁可能);②在较宽频带内只有一个交点(不会出现误跟踪及锁死);③交点对应频率为ωs(跟踪准确).若此 3个条件均得到满足,则验证了文中对PLL4种跟踪失效分析的正确性,以及所提出的静态电容补偿法的可行性与实用性.作为对照,在图中一并给出了阻抗分析仪测量到的换能器整体相位曲线和换能器加载时的机械谐振频率.

测量结果如图5(a)～(d)所示.图中,fs为阻抗分析仪所测的换能器带载机械谐振频率;fz为超声电源所测的机械臂相位特性曲线θ1(ω)过零点的对应频率;f1和 f2为阻抗分析仪所测的换能器整体相位曲线的低相位零点频率和高相位零点频率.

图5(a)为换能器空载时的测量结果.阻抗分析仪显示换能器整体相位曲线存在两个相位零点频率f1和f2,二者间距 502Hz,可能发生误跟踪.而超声电源所测曲线只有一个零点 fz,不存在误跟踪的可能.fz与f1非常接近(可视为同一点),二者误差均为-5Hz,故当换能器空载时,用传统PLL和文中所提出的基于静态电容补偿法的 PLL都能实现准确跟踪,而后者不会发生误跟踪.

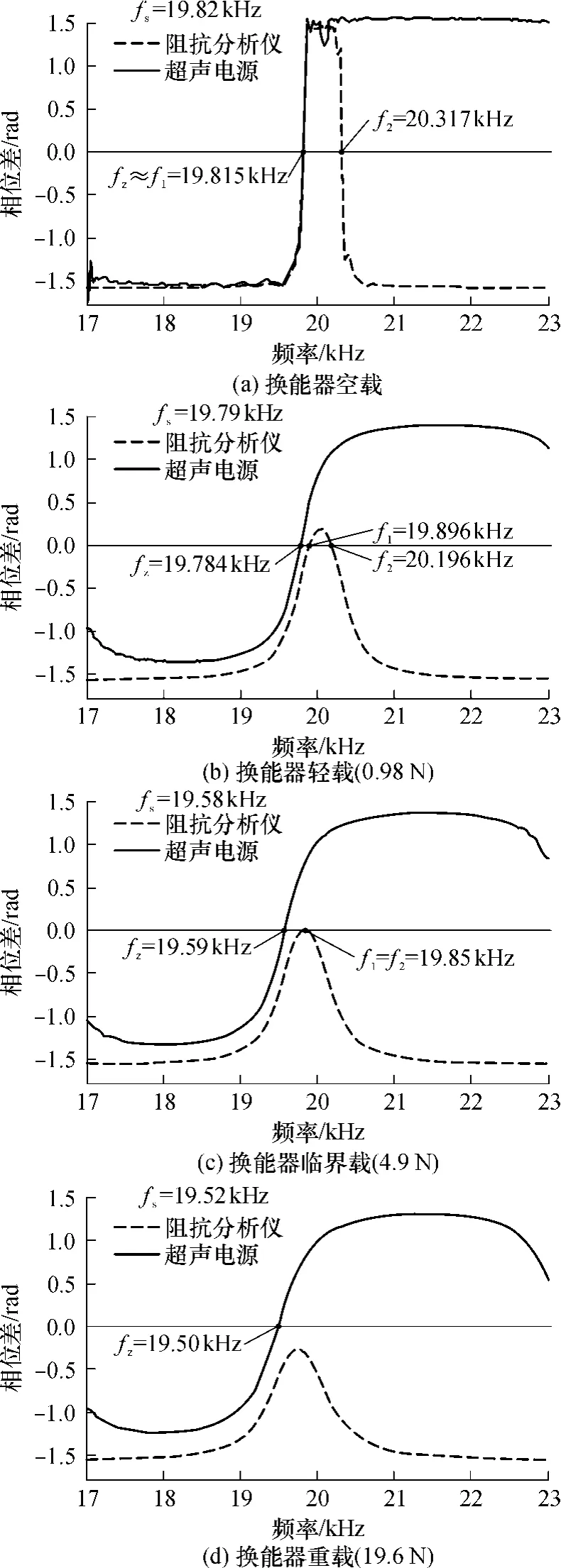
图5 基于文中理论和传统PLL的换能器相位特性对比实验Fig.5 Comparing experiments for transducer'phase character based on theory presented and traditional PLL

图5(b)为换能器轻载时(荷载力为0.98N)的测量结果.由于带有负载,换能器机械品质因数降低,整体相位曲线趋于平滑,f1和f2间距减至 300Hz,发生误跟踪的可能性加大.f1与fs相差106Hz,即此时传统PLL跟踪误差为106Hz.而超声电源测得的曲线依然只有一个零点,不存在误跟踪,并且跟踪误差为-6Hz.

图5(c)为施加4.9N荷载力的情况.换能器整体相位曲线与横轴相切,f1与 f2重合,即将发生失锁,故称临界载,此时传统 PLL的跟踪误差可达270Hz.而超声电源测量的结果依然稳定,跟踪误差为10Hz.

图5(d)为换能器重载(荷载力为19.6N)情况.换能器整体相位曲线与横轴失去交点,f1和 f2消失,传统PLL处于失锁状态,跟踪功能失效.而超声电源所测得的换能器机械臂相位曲线仍然较为理想,跟踪误差为-20Hz.

换能器带载时,采用文中理论得到的机械臂相位曲线在设定频率范围的低端和高端并不十分理想,这在一定程度上限制了文中所提出跟踪技术可能达到的最大跟踪带宽,但对跟踪精度影响较小.

实验结果表明,文中所论及的压电换能器锁相环频率跟踪失效理论与事实相符,基于静态电容补偿法所研制的超声电源测得的换能器机械臂支路相位特性与理论预期吻合较好.

4 结论

针对传统换能器锁相环频率跟踪技术中存在的跟踪失效现象,提出一种宽带下的静态电容补偿法,通过补偿换能器静态电容的分流作用,使换能器对锁相环呈现出理想的LCR串联谐振回路特性.基于该技术研制了数字化跟踪超声电源,对某换能器进行了不同负载下的跟踪精度测试.结果显示:不论在换能器空载、轻载、临界载还是重载时,都能保持所测曲线有且必有一个相位零点,并可较为准确地跟踪机械谐振频率,大大缓解跟踪失效问题.该技术为碳纤维复合材料超声振动加工领域提供了新的换能器频率跟踪控制方法.

[1] 张崇峻,董惠娟,张广玉,等.超声振动钻孔半波长振动系统的设计 [J].哈尔滨工业大学学报,2001,33 (3):329-332.

Zhang Chong-jun,Dong Hui-juan,Zhang Guang-yu,etal. Design of a half-wave vibration system for ultrasonic d rilling[J].Journal of Harbin Institute of Technology, 2001,33(3):329-332.

[2] 董惠娟,张广玉,董玮,等.压电超声换能器电端匹配下的电流反馈式频率跟踪 [J].哈尔滨工业大学学报, 2000,32(3):115-122.

Dong Hui-juan,Zhang Guang-yu,Dong Wei,et al.Current feedback frequency tracking control with matching of piezoelectric[J].Journalof Harbin Institute of Technology, 2000,32(3):115-122.

[3] 鲍善惠,王敏慧.超声波发生器的频率跟踪电路 [J].洗净技术,2003(10):3-6.

Bao Shan-hui,Wang Min-hui.Frequency tracking circuit for ultrasonic generator[J].Cleaning Technology,2003 (10):3-6.

[4] Mortimer B,du Bruyn T,Davies J,et al.High power resonant tracking amplifier using admittance locking[J].Ultrasonics,2001(39):257-261.

[5] Pons JL,Ochoa P,Villegas M,etal.Self-turned drivingof piezoelectric actuators:the case of ultrasonic motors[J]. Journal of the European Ceramic Society,2007(27): 4163-4167.

[6] 王艳东,李赫,王敏慧,等.锁相环跟踪超声振动系统谐振频率的改进 [J].声学技术,2007,26(2):253-256.

Wang Yan-dong,Li He,Wang Min-hui,et al.Improving PLL tracking of u ltrasonic vibration resonant frequency [J].Technical Acoustics,2007,26(2):253-256.

[7] Yoko Mizutani,Taiju Suzuki,Hiroaki Ikeda,et al.Power maximizing of ultrasonic transducer driven by MOS-FET inverter operating at 1 MHz[C]∥Proceedings of the 1996 IEEE IECON 22nd International Conference.Los Alam itos:IEEE,1996:983-986.

[8] 刘荣光,李晓谦,胡仕成,等.超声振动系统导纳特性与声场指向性研究 [J].振动与冲击,2008,27(7): 154-157.

Liu Rong-guang,Li Xiao-qian,Hu Shi-cheng,et al.Study on admittance character and sound field directive property of u ltrasonic vibration system[J].Journal of Vibration and Shock,2008,27(7):154-157.

[9] Yoko Mizutani,Taiju Suzuki,Hiroaki Ikeda,et al.Automatic frequency control for maxim izing RF power fed to ultrasonic transducer operating at 1MHz[C]∥Industry Applications Conference.Piscataway:IEEE,1996:1 585-1588.

[10] 林书玉,张福成.压电超声换能器的电端匹配电路及其分析[J].压电与声光,1992,14(4):29-38.

Lin Shu-yu,Zhang Fu-cheng.Analyses ofmatching circuits of piezoelectric ultrasonic transducers[J].Piezoelectrics＆Acoustooptics,1992,14(4):29-38.

[11] 武剑,董惠娟,张广玉.基于静态电容补偿的压电换能器锁相环频率跟踪 [J].大连海事大学学报,2009, 35(1):57-61.

Wu Jian,Dong Hui-juan,Zhang Guang-yu.A PLL-dependent piezoelectric transducer frequency tracking technique based on static capacitance compensation[J].Journal of Dalian Maritime University,2009,35(1):57-61.