地铁列车着火后在隧道内行驶的安全速度*

郗艳红 毛军 樊洪明 赵耀华 朱升

(1.北京交通大学土木建筑工程学院,北京 100044;2.北京工业大学建筑工程学院,北京 100022)

地铁列车在隧道内着火后,迫停在隧道内就地实施人员疏散和救援的难度较大.目前一般规定列车应尽可能地行驶到前方车站实施抢险救援[1].列车携带火源行驶时,会形成迎风气流,有两种可能:风助火势而使火势增强、反而扩大危害;气流破坏燃烧过程或降低燃烧物的温度至燃点以下,火焰减弱甚至熄灭.Carvel等[2]的研究表明,纵向通风对隧道内重型货车引起的火灾影响最大,相比于自然通风, 3m/s的纵向风速可以使火灾的热释放速率(HHR)增大 4.5倍,因此应采用控制烟雾所需要最小通风风速;里查德等[3]发现,隧道内大型油池火灾的规模将因纵向强制通风而增加,风速为 2m/s时比自然通风条件下的类似火灾高大约 20%,而某些较小油池火灾的规模则因强制通风而减小.关于地铁列车在机械通风时的火灾 HHR变化没有相关的研究报道.因此,列车着火后继续在隧道内行驶,既有风险,又具有一定的合理性.其关键在于火源的燃烧强度、列车的运行速度以及采取的机械通风排烟模式.杨英霞等[4]认为带着火源在隧道内行驶到前方车站进行疏散的方法存在危险.屈璐等[5]对运行中地铁列车周围的速度场进行了数值模拟,认为列车时速在25km/h以内时,列车周围气流的相对速度在5m/s以下,列车应以尽可能低的速度驶向下一车站进行救援,以避免形成太高的相对流速.这些结论未结合风速对火源热释放速率的影响,有一定的局限性.文中旨在对此进行进一步研究,以便为隧道列车火灾的应急处置提供必要的参考.

1 隧道列车火灾火源处的气流速度

列车在隧道内以速度vt行驶时,在列车前方形成风速为v的活塞风,如图1所示.

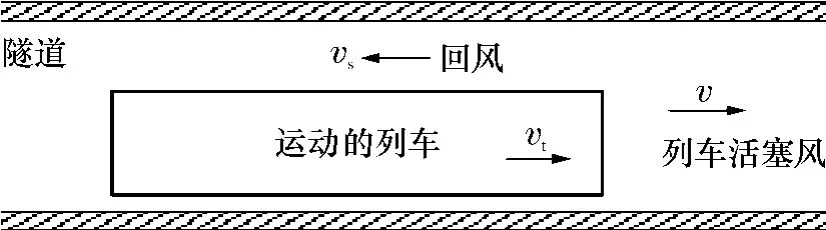
图1 地铁列车在隧道内行驶产生的活塞风和回风Fig.1 Piston wind and backflow in subway tunnelgenerated by moving subway train

隧道与列车之间的环形空间的平均风速为 vs,相对于列车的风速为vsr=vt+vs.因为火源随列车一起运动,所以气流相对于火源的风速也为 vsr.设 α为列车横断面积At对隧道横断面积A的比值,即阻塞比,则根据连续性方程可得[6]:

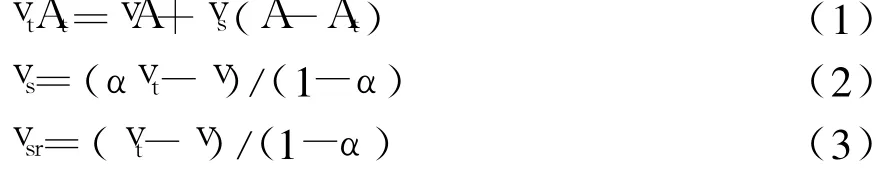
而

由上可得:

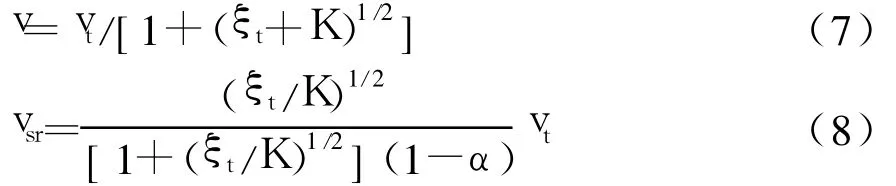
或

式中:ξt为除环状空间外的隧道段的阻力系数;为沿程阻力系数;L和Lt分别为隧道和列车的长度; d、ds分别为隧道和环状空间的水力直径;K为活塞作用系数;ξ为气流由车站进入隧道的局部阻力系数;ξ1、ξ2分别为气流由隧道段进入环状空间或由环状空间进入隧道段的局部阻力系数.

2 气流对火源强度的影响

假设地铁列车顶部着火,并形成火焰,列车着火后从隧道行驶并停留在站台上的情况.气流以速度vsr流过火源时,既可能以对流、导热和吸收辐射热的方式带走火灾的部分热量,降低火灾的温度,使火灾强度减弱;也可能增加供氧量,促进分子运动速度加剧,使可燃物和氧分子接触面及接触几率增大,使燃烧强度增大.因此,气流对火灾强度有直接影响,应存在最佳流速,使火灾强度达到最小.

2.1 气流流经火源的换热计算

低温强迫气流流经火源时,烟气与冷空气之间对流换热,同时,冷空气裹挟烟气流动引起质量传递导致热量变化.以列车中部及头部着火为例进行计算.

(1)对流换热.

对流带走的热量为[7]

式中:a为对流换热系数,a=Nu k/d;k为空气导热系数;Nu为强迫对流的努塞尔数,Nu=0.664Re1/2◦Pr1/3;Re为雷诺数,Re=vd/ν;运动粘度ν、普朗特数Pr和空气导热系数k分别为:ν(Tf)=(-6.6393+

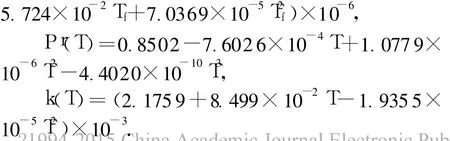
式中:Tf、Tt分别为环形空间内火焰和气流的温度.

(2)质量传递引起的热量变化.

强迫气流裹挟热烟气流动即质量传递导致的热量变化与冷空气的流量有关.

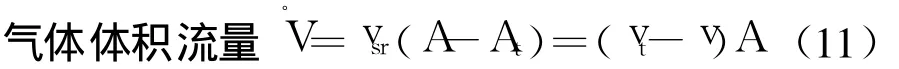
则气流带走的热量为

式中:ρ0为常温(300K)气流的密度,kg/m3;cp为气流的比热,J/(kg◦K),与烟气的温度有关,cp(T)= 1.0486-3.207 5×10-4T+7.148 8×10-7T2-2.9844×10-10T3;ΔTr为气流流经火区前后的温度差.

(3)风速增大引起的释热增量.

对于隧道受限空间内的燃烧,风速较大时,燃烧可能由燃料控制转变为通风控制,氧气输送量的增加或者可燃物和氧分子接触面及接触几率的增大,都可能使释热增加,前者可以通过化学方程计算,后者产生的释热量增量为Δqa,可通过实验得出.

2.2 燃料燃烧的热释放速率

若隧道内的氧气足够燃料燃烧反应之用,则燃料可充分燃烧,风速为 v时的热释放速率可表示为[7-9]

式中:φ为可燃物的燃烧效率,%;ΔH为可燃物的热值,kJ/g;m˙为质量损失速率,g/s.

此时,送风气流导入的氧气对燃烧强度的影响并不显著.设无风时的热释放速率为Q0,则有:

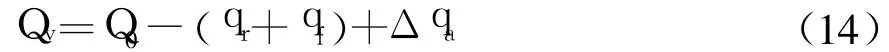
式(8)表明,风速较低时,气流带走的热量较少,对火源强度的影响不大;风速达到一定值时,虽然可燃物和氧分子接触面及接触几率增大,释热可能增加,但气流带走的热量也增多,燃烧强度仍可能下降;风速继续增大时,燃烧由燃料控制转变为通风控制,火源的强度受风速的影响较大,释热量可能增大.

3 气流影响热释放速率的模型实验

由于客观条件的限制,难以在现场进行隧道列车火灾的全尺寸试验,因此,采用 1∶8模型实验,再通过相似变换对原型进行研究.此模型比例尺可以保证与原型实验的相似性和精度.

3.1 主要物理量的相似关系

在隧道列车火灾中,浮力效应起主导作用,火源附近的烟气流动为重力流;在机械通风的条件下,离火源较远处的气流是压力流,但由于雷诺数较大、容易进入阻力平方区,雷诺准则自动满足.因此,采用弗劳德准则作为相似准则,温度比例尺确定为 1.

设几何比例尺为Lm/Lr=1/8,则由Fr准则得:(gmLm)=/(grLr);速度关系:vm=vr(Lm/ Lr)0.5;热释放速率关系:Qm=Qr(Lm/Lr)2.5.其中:L为几何尺度,m;Q为热释放速率,kW;g为重力加速度,m/s2;下标m代表模型,r代表原型.

热释放速率是火灾的主要决定因素,表征火势的大小.地铁火灾规模通常为Qr=0～10MW,地铁设计规范一般将热释放速率取为 5MW[10].据相似关系式得到模型的火源热释放速率为Qm=0～55kW.

3.2 隧道模型实验介绍

根据相对运动原理,列车携带火源运动时在列车前部产生同向运动的气流,相当于列车和火源静止、隧道运动、速度近似相等的气流流向列车的情况.由于使整个隧道运动是困难的,因此,在模型实验中使隧道静止.图2表明,此时可以反映气流速度对火源强度的影响.地铁列车一般的运行速度不超过70km/h,马赫数不超过0.057,因此不需考虑压缩波的影响.

图2 利用相对运动原理分析气流对火源影响原理图Fig.2 Piagrams of the principle of the relativemovement being used to explain the impacts on the fire sourcemade by airflow

采用正庚烷作为燃料,其密度为0.6594kg/m3,则有:

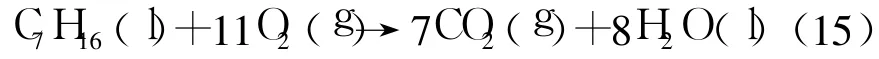
定压摩尔热qp=-4817.03kJ/mol;经过换算可得ΔH=48.24kJ/g;查表φ=93%[7].由式(13)计算热释放速率.

实验装置主要包括围护结构、通风排烟系统、温度和烟气化学成分测量系统以及数据采集系统等,如图 3所示.围护结构的耐火极限高且在燃烧时无有毒气体产生.采用变频控制的离心风机提供风流模拟列车在隧道里的运动,调节风机的频率改变风速,相当于改变列车的运动速度.调节频率为0～50Hz.油盘直径为250mm,每次燃烧燃料250mL.支承油盘的支架安放在电子天平上,燃料质量随时间的变化被实时监测,采样间隔为10s,燃烧时间2～10min,通过换算得到质量损失速率m˙.同时,检测隧道内的烟气温度和烟气成分,烟气采样周期为 1 s.对火焰变化和烟气逆流实时录像和观测,录像帧频为 25帧/s.采用电子风速仪测定模型内的气流速度.新风来流速度相当于列车在隧道内运动时的活塞风风速.由此换算环形空间过流断面的平均风速,进而分析风速与热释放速率之间的关系.

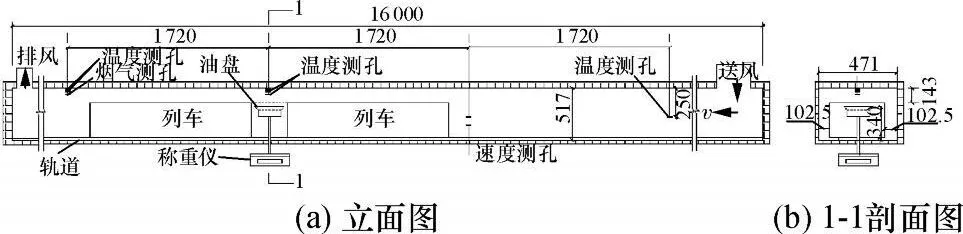
图3 地铁隧道模型实验装置主体及测量系统Fig.3 Experimental setup of themain subway tunnelmodel and measure system

3.3 模型实验的测试数据

按表 1中的实验条件进行了模型实验,以便分析不同的列车运行速度对火灾热释放速率和烟气流动特性的影响,以及不同的列车运行速度对列车上不同着火部位的火灾特性的影响.表1中,C为烟气浓度.

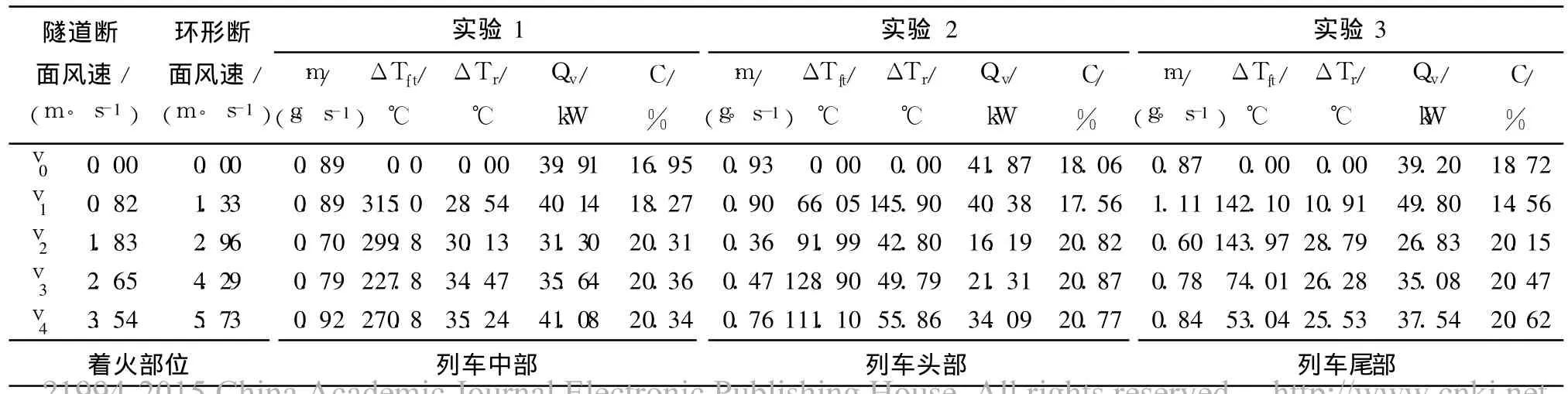
表1 不同风速下的热释放速率和含氧浓度Table 1 HRR and oxygen concentration at different ventilation velocities

4 实验数据处理及结果分析

首先需要判定在没有机械通风的情况下,隧道模型内的空气含氧量是否能保证 250mL的正庚烷燃烧所需.根据化学方程式(15)可计算其耗氧量:

隧道模型内在无机械通风条件下的含氧量为

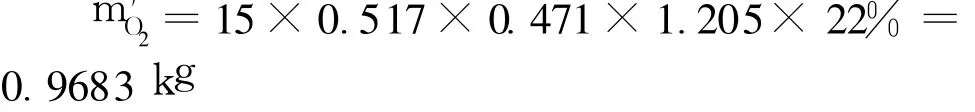
可见,mO2＜m′O2,由表 1可知,在实验工况的各风速下,氧气的浓度最低为 14.56%,最高为20.87%,均高于燃烧所需的最低氧浓度 13%,因此,燃烧可以充分进行,因通风引起的含氧量增加不对燃烧释热起明显作用,所以释热量增加主要是因氧气分子与正庚烷分子的接触面和几率增加而引起的[11].

此外,可以计算出各工况下的对流换热、质量传递换热,以及风速增大引起的释热增量,参见表 2.气流流经着火区域时由对流换热所带走的热量 qf少于冷空气注入因质量传递换热所带走的热量qr. qr随速度的增加而增加,且释热增量 Δqa也增加.如果qr＞Δqa,则一定风速下的释热速率小于零风速下的释热速率,即Qv＜Q0;反之,Qv＞Q0,例如风速为0.82m/s和3.54m/s的情况.

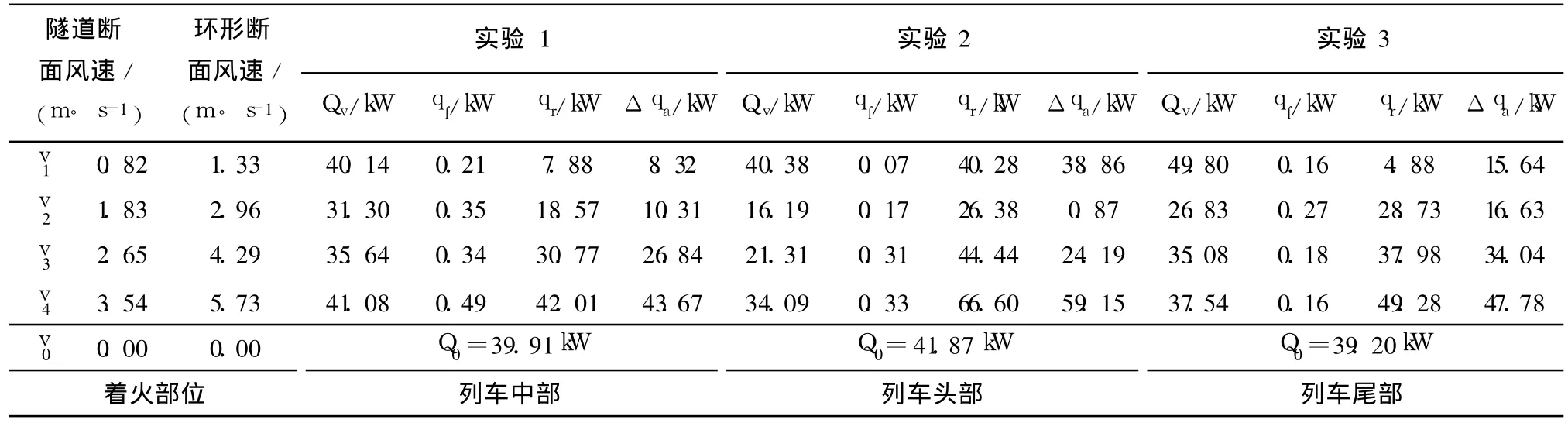
表2 不同风速下的对流换热、导热和辐射换热以及释热增量Tab le 2 Convection,conduction and radiation heat and incremental HRR at different wind velocities

4.1 速度对火源燃烧特性的影响

根据实验可得到曲线图 4～7.着火列车在隧道内行驶的速度对火源强度和烟气流动特性产生显著影响,需确定列车携带火源运行的最合理速度.

图4表明,热释放速率随速度增加先缓慢上升,随后快速减小.存在某一风速(v2=1.83m/s),使对应的热释放速率最小.图 5表明,在风速较低的情况下,氧气浓度随着燃烧时间的延长而逐渐降低,氧气浓度随着速度的增大而增加.当速度增大至某一值时,氧气浓度保持稳定,速度超过该值时也是如此.即存在最低风速(v2=1.83m/s),使气流中氧气浓度不随时间的变化而降低,烟气浓度不再增大.

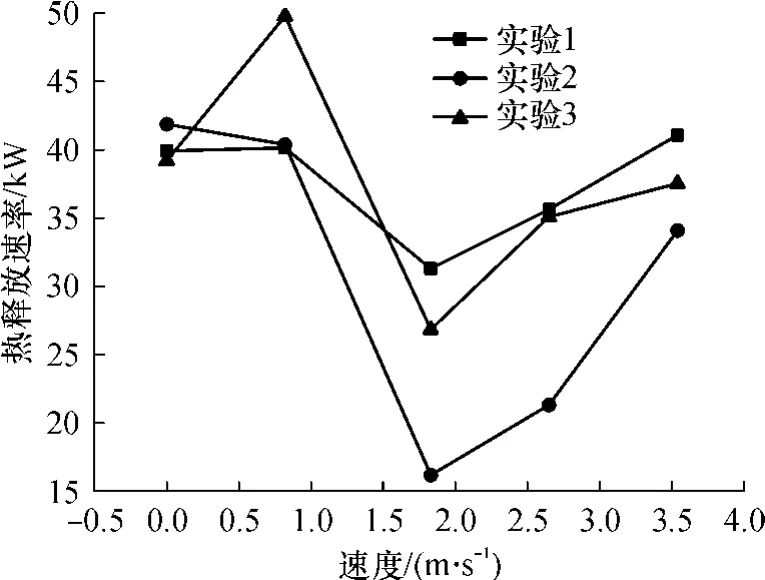
图4 热释放速率随速度变化曲线Fig.4 Heat release rate-speed curves

由图 4可知,在火源高度相同的情况下,风速对热释放速率均有明显的影响.但无论是列车的头部、中部还是尾部着火,尽管热释放速率的时变曲线不同,热释放速率与风速的关系曲线的变化趋势却比较接近,且均在v2=1.83m/s左右达到最小值.因此,最佳风速对列车的着火部位并不敏感.这有利于对列车着火后在隧道继续行驶的速度进行控制.

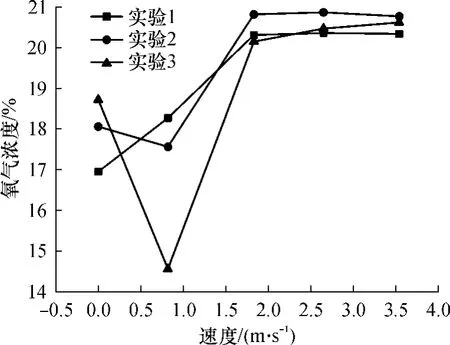
图5 氧气浓度随速度变化曲线Fig.5 Oxygen concentration-speed curves

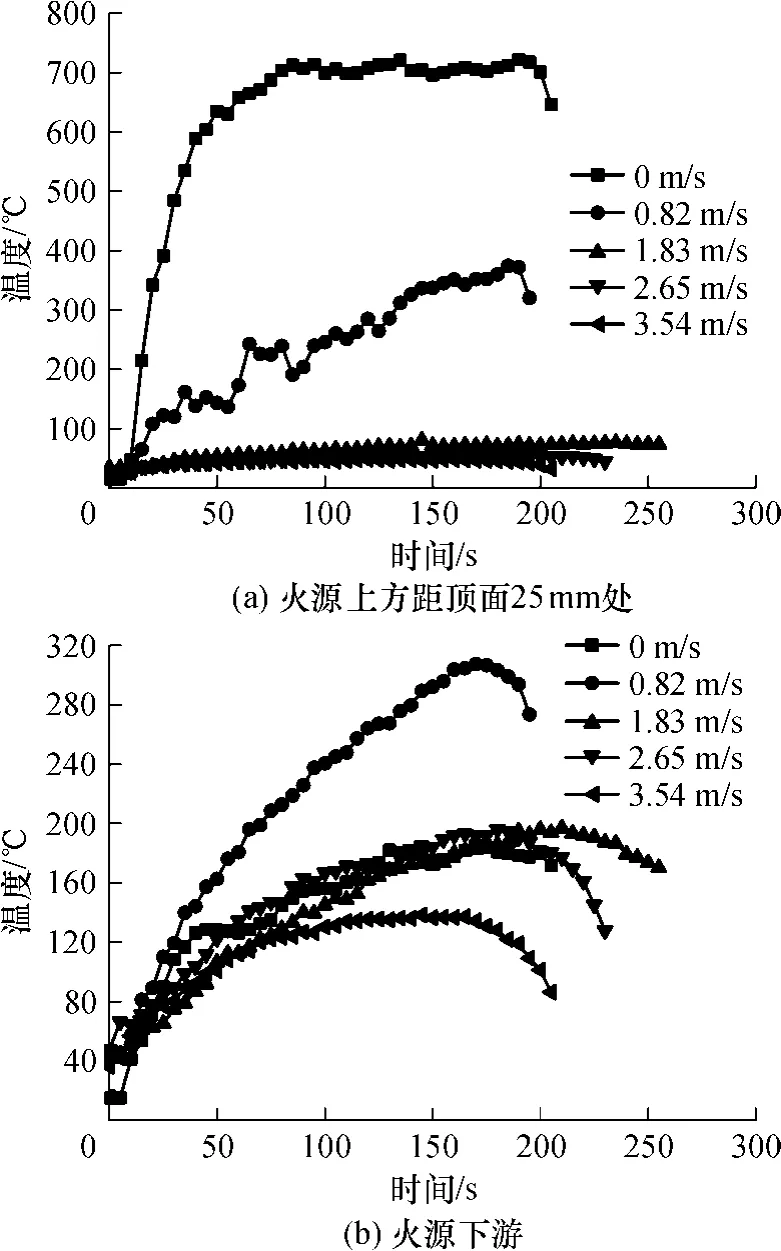
图6 实验 1中温度随时间的变化关系Fig.6 Relationships between the temperature and time in case 1

图7 实验 1中不同风速下的火焰传播Fig.7 Flame extension at different ventilation velocities in case 1

图6为实验1中温度随时间的变化曲线.图6表明,在风速较低(0.82m/s)的情况下,火源上方的温度可高达 400℃,风速对温度的影响比较大;当风速逐渐增大至某值(1.83m/s)时,该温度快速降低,随后变化平缓;风速继续增加,温度时变曲线的规律不变.即存在一个最低风速时,低于该风速时,火源上方的烟气温度高且变化快;高于该风速时,火源上方的温度变化平缓,温度保持稳定.由图 6、7知,火源下游在风速较低(0.82m/s)时的温度高于自然通风条件下的温度.原因是:后者的火焰呈对称形式并稳定在一定的范围内;而前者的火焰向下游偏转和扩展,高温烟气流过该点致使温度升高;风速继续增大,由于风流带走的热量增加,该点的温度又随风速的增大而下降.图 7说明,在风流的作用下,火焰发生偏转并向下游扩展一段距离,在风速达到0.82m/s以后,火焰偏向一侧,烟气逆流基本消失.根据Oka和Atkinson公式[12]可以计算出本实验中的临界风速为0.79m/s,当风速为1.83m/s时,不会出现烟气逆流的情况.

因此,与最小热释放速率和良好烟流特性相对应的风速值应为v2=1.83m/s,该风速下的烟气温度、烟气浓度已下降到较低的水平,而且继续增大风速,变化已经比较小,同时,烟气不产生逆流.

风速对火源上方和下游的温度以及烟气浓度的影响比较大,在某个风速值时,温度变化率和烟气浓度变化率显著增大,温度和烟气浓度快速下降;超过该风速值后,继续增加风速,温度和烟气浓度变化平缓.

4.2 地铁列车着火后在隧道内行驶的速度限值

热释放速率是描述火灾过程的重要参数,是决定火灾危险的基本因素.上述分析表明,列车着火的热释放速率在v2=1.83m/s时达到最小值.

在燃料用量相同的情况下,列车头部和中部着火,临界速度均约为 0.82m/s,尾部着火时的临界速度约为1.38m/s.列车着火部位相同的情况下,改变燃料用量,临界风速相同.相比其它速度,当风速为1.83m/s时,氧气浓度较高,火源上方和下游的温度均较低,且无烟气逆流;无论火源在车头、车中还是车尾,该风速下,列车向前行驶较为安全.该风速即为列车以某安全速度vt运动时的活塞风风速.

根据式(1)～(9)求出模型列车的速度:

活塞风风速vm=1.83m/s,

活塞作用系数km=1.535,

模型列车速度vtm=3.975m/s.

由速度相似关系得原型列车速度:

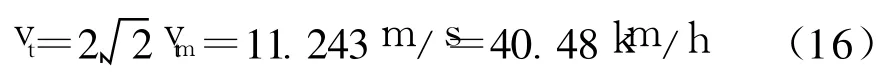
也可直接计算原型列车的速度.根据文献[6],若列车长度大于150m,活塞作用系数按下式计算:

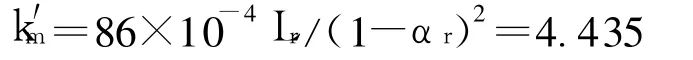
其中:αr为原型的阻塞比.

原型的活塞风速:

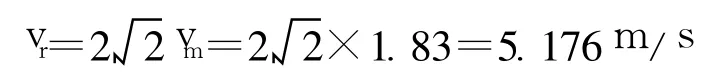
则原型列车速度由式(9)计算得:

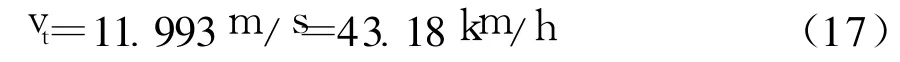
可见,两种方法计算得到的列车速度(16)、(17)非常接近,相差不超过6.5%,取两者的平均值作为最终的原型列车速度.即原型列车运行的活塞风风速是18.63km/h,对应的原型列车安全速度为41.83km/h.

5 结论

通过模型隧道内的油池火灾实验得到了风速与火灾热释放速率的关系:存在某一优化风速值,使火灾的热释放速率最小.风速低于该值,热释放速率减小,温度和烟气浓度快速下降;反之,热释放速率增大,继续增加风速,温度和烟气浓度变化平缓;风速达到该值不会使火势增强和烟气逆流.文中隧道列车火灾模型实验中,该优化速度为v=1.83m/s,该值对应于模型列车运行时产生的活塞风风速.因此,模型列车的活塞风风速不宜超过该值.

同时发现,在风速达到优化值时,模型列车不同部位着火时的热释放速率虽然不同,但均为该部位的最小热释放速率;温度和氧气浓度也对人员安全有利.这有利于制订应急预案对列车着火后继续行驶的速度实行统一控制.

根据上述模型实验,以北京地铁 1、2号线的隧道列车火灾为原型,通过相似变换可得到列车着火后继续行驶的优化速度——即列车着火后的运行安全速度,约为41.83km/h.不过,若是列车头部着火,应考虑活塞风推动部分烟气向前运动的情况.

[1] 王铭珍.国外地铁如何防火[J].山东消防,2003,4:9-10. Wang Ming-zhen.How to prevent fires in abroad[J]. Shandong Fire,2003,4:9-10.

[2] Carvd R O,Beard A N,Jowitt PW.The influence of tunnel geometry and ventilation on the heat release rate of fire[J].Fire Technology,2004,40(1):5-26.

[3] 里查德◦卡维尔,阿兰◦比尔德,保尔◦乔威特.隧道突发火灾时的明智通风控制 -纵向通风对放热速率的影响 [J].王晔,译.消防技术与产品信息,2001 (9):46-49.

Richard Carville,Alan Beard,Paul Qiao Weite.The intelligentventilation control at the time of tunnel fire-In fluence of Longitudinal Ventilation on HRR[J].Wang Ye, translation.Fire Technique and Products Information, 2001(9):46-49.

[4] 杨英霞,陈超,屈璐,等.关于地铁列车火灾人员疏散问题的几点讨论 [J].中国安全科学学报,2006,16 (9):45-50.

Yang Ying-xia,Chen Chao,Qu Lu,et al.Discussion on some problems of evacuation from metro train fire[J]. China Safety Science Journal,2006,16(9):45-50.

[5] 屈璐,陈超,杨英霞,等.地铁列车区问隧道着火时行车安全性的讨论 [J].地下空间与工程学报,2003,3 (5):832-836.

Qu Lu,Chen Chao,Yang Ying-xia,et al.Discussion about safe velocity of on-fire train in subway tunnel[J].Chinese Journal of Underground Space and Engineering, 2003,3(5):832-836.

[6] 金学易,陈文英.隧道通风及隧道空气动力学 [M].北京:中国铁道出版社出版,1983.

[7] 范维澄,王清安.火灾学简明教程 [M].合肥:中国科学技术大学出版社,1995.

[8] 钟委,霍然,史聪灵.热释放速率设定方式的几点讨论[J].自然灾害学报,2004,13(2):64-69.

Zhong Wei,Huo Ran,Shi Cong-ling.Some discussion on methodology to design heat release rate[J].Journal of Natural Disasters,2004,13(2):64-69.

[9] Roh JS.An experimental study on the effect of ventilation velocity on burning rate in tunnel fire-teptane pool fire case [J].Building and Environment,2008,43(7):1225-1231.

[10] GB50157—2003.地铁设计规范[S].

[11] Kuldeep Prasad,Yuji Nakamura.Effect of wind velocity on flame spread in microgravity[C]∥Proceedings of the Combustion Institute.USA:[s.n.],2002:2 553-2560.

[12] Oka Y,Atkinson C T.Control of smoke flow in tunnel fires[J].Fire Safety Journal,1995,25(4):305-322.