基于半圆试件的沥青混合料动态模量测试方法*

刘宇 张肖宁 陈少幸

(1.华南理工大学土木与交通学院,广东广州 510640;2.广东交通集团检测中心,广东广州 510420; 3.中南大学土木建筑学院,湖南长沙 410083)

沥青混合料作为一种典型的黏弹性材料,其动态模量不仅反映了应力与应变的力学性质,更主要是反映了不同荷载下材料的动态响应特性.新版的基于力学-经验法的AASHTO 2002沥青路面设计指南即采用单轴压缩动态模量作为其基本材料参数,近几年研究者逐渐意识到单轴压缩试验测定的动态模量用于新建路面质量评价和路面维修改造中存在这样一个问题,即通常沥青层厚度不能够产生单轴压缩试验所需要的150mm高的试件,导致设计标准中采用的单轴压缩动态模量不能被用于对设计的符合性检验[1]中.采用间接拉伸动态模量替代弯拉模量来分析结构层底的弯拉应力或弯拉应变也缺乏充分的依据,试验方法不同,测定的沥青混合料动态模量也不同,而取值不同又会影响路面结构层的应力、应变和位移技术,从而影响沥青路面的结构设计,因此需要建立用于弯拉模量符合性检验的动态模量试验方法.

目前,对路面芯样进行室内试验分析仍是对已建成路面进行质量评价的最主要技术手段.近年来,在欧洲和美国,一种采用路面芯样为试验标本的半圆弯曲试验方法(Semi-Circular Bending Test,简称SCB试验)越来越引起人们的注意,这种试验方法可以对多种成型方法的沥青混合料进行分析和评价,尤其是可以对路面芯样进行方便快捷的多种目的试验.半圆弯拉试验原用于岩石力学性能的研究[2],后由 Krans等[3]引入到沥青加铺层的设计中,用于评价加铺层的抗裂性能;Mull等[4]采用带切口的半圆试件评价了橡胶沥青混合料的抗裂性能; Bayomy等[5]采用带缺口的半圆试件评价了34种沥青混合料路面芯样的抗裂性能.

目前,在沥青混合料性能研究中,半圆弯曲试验多用于测定断裂韧度和弯拉强度,而用于系统地测定动态模量仍罕有报道,采用半圆弯曲试验方法测定混合料的动态模量,会为对已建成路面质量对设计的符合性检验建立一种有效方法和技术手段.文中研究开发了半圆弯曲试验动态模量测定方法,采用开发的方法测定了常用沥青面层混合料的动态弯拉模量,对试验数据的一致性和有效性进行了深入分析.

1 试验参数选择

1.1 试验装置

半圆弯曲试验装置如图 1所示.在半圆形试件的底部有两个圆棒作为支点,支点的距离随试验要求而定,在半圆试件上部居中位置用圆棒加载.采用圆棒作为支点和加载可以减少试件与边界之间的摩擦力,使试件边界条件简单化.

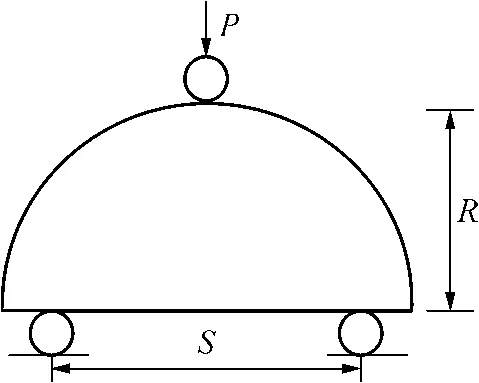
图1 SCB试验装置Fig.1 SCB test facility

1.2 支点间距选择

由半圆弯曲试验的受力状态可知,在较大的支点间距下可以得到较大的应力响应,试验时希望施加的荷载较小而又有较大的应力响应,较小的荷载会减小加载处和支点处的凹陷变形,而支点间距过大,接近试件边缘时会导致支点处剪切面过小而出现剪切破坏,如图 2所示.由预备试验确定支点距离不宜超过0.9倍直径,试验中选择支点间距为0.8倍直径.

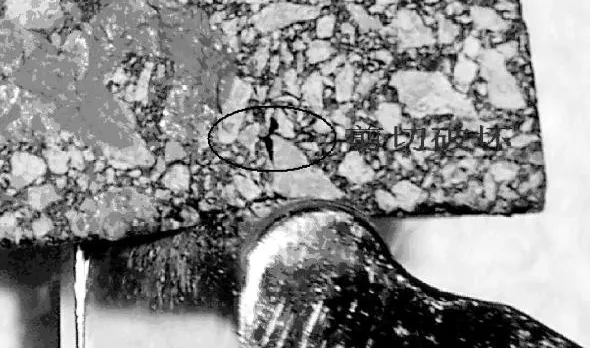
图2 支点处剪切破坏Fig.2 Shearing damage of bearing

1.3 切割允许偏差分析

半圆试件一般由一个圆形试件切割形成,在切割过程中会由于锯片厚度和切割损耗导致试件出现缺失,需要对此造成的误差进行分析来选择切割工艺.基于二维平面假设,以直径100mm试件,支点间距80mm为例进行切割损耗后试件的应力响应计算,分别假设半圆试件损失为1.0、1.5、2.0和3.0mm,查看试件底部中心拉应力 S11的变化.分析时取弹性模量E=1000MPa,泊松比μ=0.30,施加荷载为1N/mm的线荷载.

由表1可以看到,当半圆试件切割损耗为1.0mm时导致的偏差为2.95%,当切割损耗为1.5mm时导致的偏差为4.63%,当损耗达到3.0mm时引起的误差已经超出了10%以上.这就要求切割锯片厚度最少控制在2.0mm以内,切割的误差及磨耗控制在0.5mm以内,则半圆试件的切割损耗及误差和可以控制在1.5mm之内,由此引起的计算误差不超过5%.

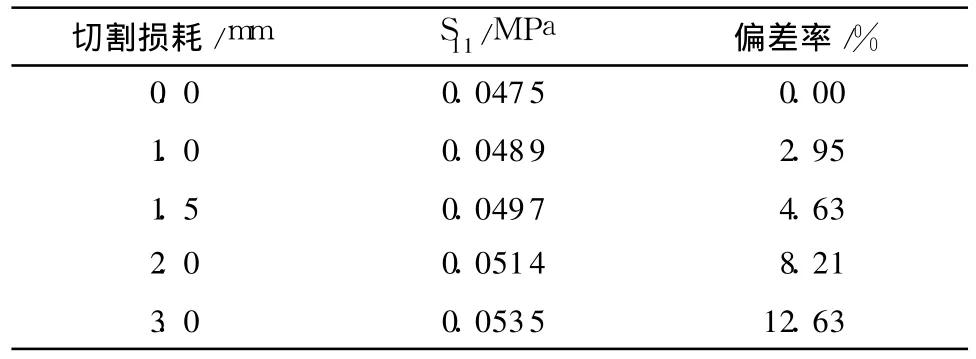
表1 切割损耗引起的计算偏差Table 1 Calculation deviation caused by the incision ullage

1.4 试件厚度选择

在力学分析时,常对试件进行平面应力假设或平面应变假设,而实际的试件厚度即非极薄也非无穷厚,试验时希望得到一个稳定的试验结果就需要分析试件厚度对试验结果的影响.按不同试件厚度分别建立三维有限元模型,选取C3D20单元.模拟半圆弯曲试验进行沥青混合料弯拉强度评价时常采用位移控制方式施加荷载,加载速率设为50mm/min,分析荷载位移δ=0.5mm时的荷载响应.

由图3可见,在荷载位移δ=0.5mm的情况下,试件厚度为20mm时应力响应最小,随着试件厚度增加到30mm时应力响应达到最大值;在试件厚度超过30mm之后应力响应趋于稳定,试件厚度为40和 50mm时的应力响应相差不大.在进行试验时,选择试件厚度为 50mm,一方面是希望得到的试验结果是稳定的,另一方面可以减少试件厚度误差对试验结果的影响.

图3 试件厚度对应力的影响Fig.3 Influence of thickness of specimen on stress

1.5 用于计算模量的响应选择

半圆弯曲试验在荷载作用下可以得到试件底部中心点位移和应变两个容易测量的响应,这两个响应都可以反算得到沥青混合料的模量.采用位移作为响应计算模量比较简单,但需采用有限元模型进行一定荷载下的频率扫描,建立模量与位移的关系[6],应用起来比较烦琐.沥青混合料作为黏弹性材料,在荷载作用下会发生黏塑性变形,不同支点假设条件下得到的位移系数也有差别:Molenaar等[7]假设半圆试件支点位置存在一个刚性的垫块得到的位移系数为1.84,Bayomy等[5]将支点假设为刚性辊轴,得到的位移系数为 2.26,两种假设下的位移相差较大;而应力系数一个为4.8,另一个为4.888,两种假设下的应力相差较小.由以上分析可知,采用试件底部中心处的位移作为荷载的响应反算模量并不合适,而半圆试件底部应变受支点边界假设条件及支点处变形影响极小,且可以应用应力与应变的关系建立动态模量关系.

2 试验装置和试验方案

试件采用旋转压实成型方法,用芬兰产双面锯切割为厚度为50mm的试件,再将之用厚度为1.6mm的超薄金刚石切割片切割为半圆试件.采用MTS公司生产的GPM(Gage-Point-Mounted)测量系统测量半圆试件底部应变,其标距为 25.4mm,试件表面装配微型变形测定引申计,引申计距试件表面高度为6.25mm,最小量程为10-10mm.半圆形试件制作成型后,安装用于固定引申计的纽扣及定位卡槽,试验装置如图4所示.

试验采用MTS 810材料试验机进行,应变由变形测定引申计测定,荷载由 MTS荷载传感器采集,传感器最大量程为10kN.

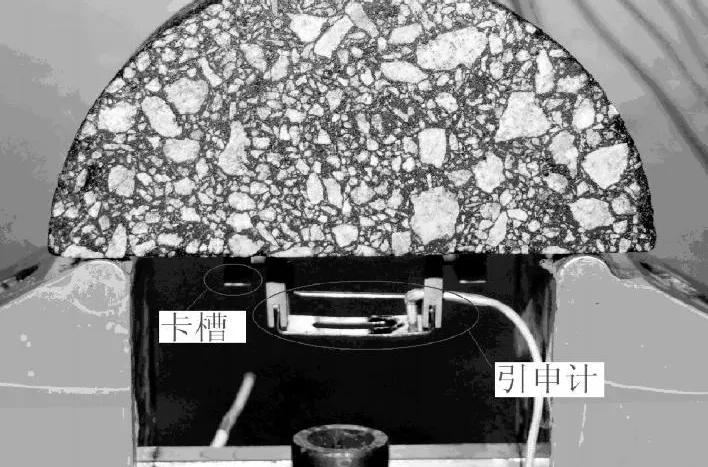
图4 半圆弯拉动态模量试验装置Fig.4 Test device of semi-circular bending dynamic modulus

对沥青路面上、中、下面层常用 3种沥青混合料进行弯拉动态模量测试,研究中选用花岗岩集料,中海油AH-70重交沥青和石灰石矿粉,各项指标均符合国家规范要求,最佳沥青含量由马歇尔试验确定, 3种沥青混合料级配如表 2所示.

表2 混合料级配及沥青用量Table 2 Gradation of asphaltmixture and contentof asphalt

采用偏正弦波荷载连续加载,试验中设置程序采集每个加卸荷循环的荷载峰值和应变峰值,为避免产生脱空现象,取最小荷载为最大荷载的5%.动态模量试验在 -10、0、5、15和 20℃下进行,每一温度下施加0.1、0.5、1.0、5.0和10.0Hz 5个频率的偏正弦波荷载,重复试验3～4次.

3 动态模量计算方法

3.1 有限元计算

半圆试件在荷载下的应力位移响应目前仍没有解析解,多采用有限元技术来得到数值解.文中基于材料的线弹性假设,获得半圆试件底部中心区域的应力系数.设模量为1000MPa,μ=0.30.三维模型模拟试验实际状况,半圆试件模型直径为 100mm,厚度为50mm,支点间距为80mm.为提高计算精度,选取20节点六面体二次完全积分单元(C3D20),种子间距设为 2.5mm,采用结构化网格划分技术,其三维拉应力分布如图5所示.

由图 5可以看到,在试件底部沿直径方向,拉应力并非均匀分布,因此需得到引伸计测量范围内的平均应力系数来进行模量计算,试件底部引申计测量范围内的应力系数如表3所示.

由表 3可见,试件底部沿直径方向应力系数由中心的4.98下降到4.56,取其均值4.81作为模量计算所需的应力系数.

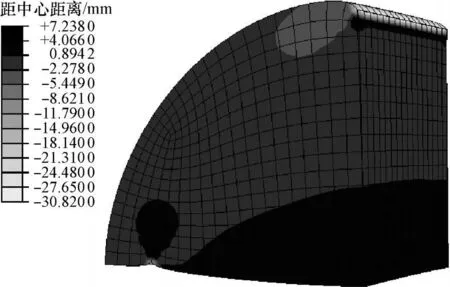
图5 半圆试件三维拉应力分布Fig.5 Three-dimensional tensile stress distribution of semi-circular specimen

表3 半圆弯曲试件直径方向应力系数Table 3 Diametrical stress factor of sem i-circu lar bending specimen

3.2 有限元结果的反算验证

平均应力与试验中测得的平均回弹应变的比值即为动态模量,但需要对试验测得的模量结果进行反算验证.这样做有两个目的:第一,因为沥青混合料为粘弹性材料,半圆试件底部应力区域并不均匀,受材料非线性的影响,试验结果会与线弹性假设的有限元结果有所差别,所以需要对试验结果进行反算来查看试验误差是否符合要求;第二,将试验中荷载传感器测得的荷载幅值和计算得到的动态模量带入三维有限元模型重新计算模型的应变响应,将之与实测结果进行对比,来验证有限元方法计算结果是否正确及精度是否符合要求.以试验中测到的AC-13沥青混合料在-10、20℃时,0.1和 10.0Hz荷载下的应变作为验证算例进行反算验证,试验时根据需要确定荷载循环次数,计算时取加载时正弦荷载的最后 5个循环的荷载均值和应变均值为计算参量,计算结果见表4.

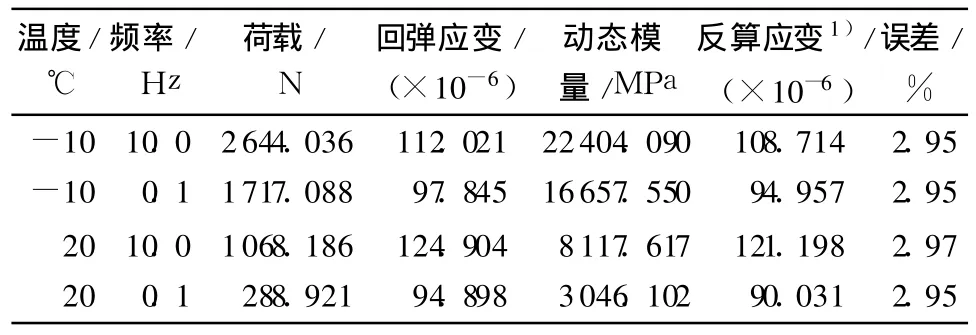
表4 有限元结果与实验结果对比Tab le 4 Contrasting of finite element resu ltswith test results

由表 4可以看到,有限元反算的结果与实际测量的结果有很好的一致性,误差都在 3%以内,计算结果有很好的精度.

4 半圆弯拉动态模量测试结果分析

4.1 常用面层沥青混合料测试结果

将AC-13、AC-20和AC-25沥青混合料在5种温度和 5种频率下测得的动态模量及相位角结果绘于图6中.每组试验进行3～4次平行试验,进行误差分析并剔差后取其平均值作为最终结果.

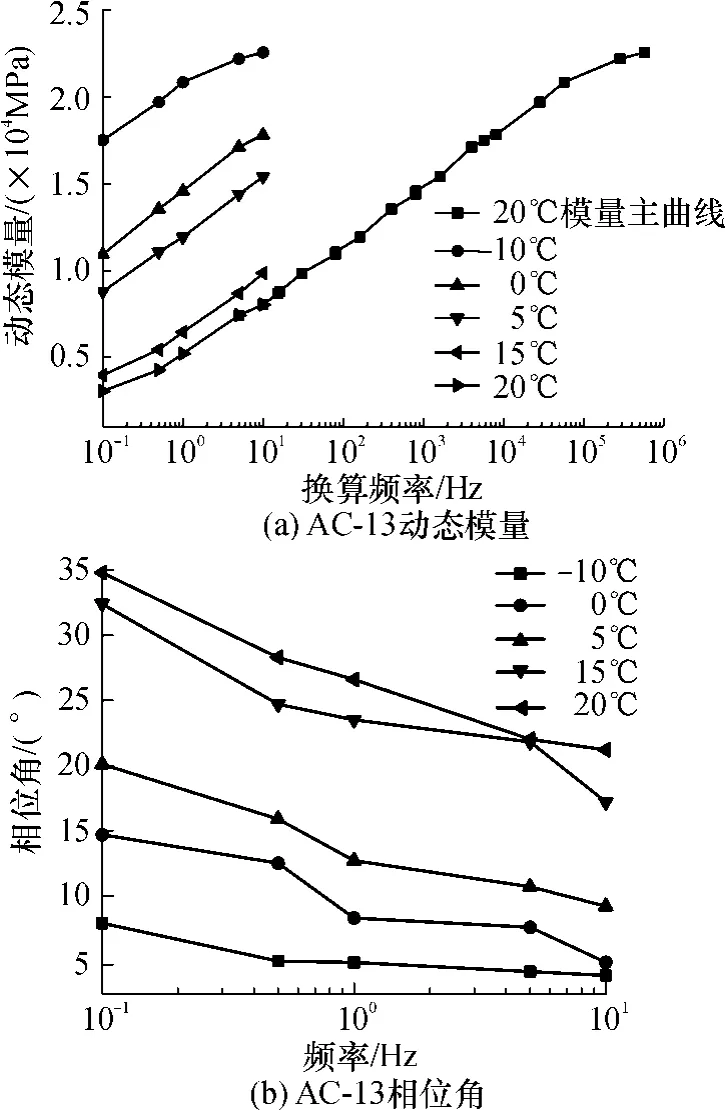
图6 沥青混合料动态模量与相位角测试结果Fig.6 Test results of asphalt mixture dynamic modulus and phase angles

由图 6可以发现,3种沥青混合料的动态模量随着频率的升高而增大,随着温度的升高而减小;沥青混合料的相位角随着频率的增大而减小,随着温度的升高而增大.这表明沥青混合料对于温度和频率敏感,其动态模量是频率与温度的函数,在工程中,频率与行车速度相关,温度与使用环境相关,将动态模量用于路面结构设计更符合工程实际状况.由图 6还可以发现,较高温度的低频部分模量与较低温度的高频部分模量有等效性,也就是说材料的应力 -应变响应关系分别依赖于温度效应与时间效应,而这种温度效应和时间效应可以通过一定的原则进行转换,也就是常说的时温转换效应.通过时温转换原则可以选择其中一个温度作为基准温度,将其它温度下的曲线沿水平方向平行左、右移动一定的距离,与基准温度下的模量曲线重合,这样可以得到该参考温度下动态模量的主曲线.图6(a)、(c)和(e)分别以 20℃为参考温度得到了 3种沥青混合料的动态模量主曲线,将动态模量主曲线进行西格摩德模型拟合(西格摩德模型为为沥青混合料动态模量;fr为参考温度下的加载频率;δ为动态模量极小值的对数; δ+α为动态模量极大值的对数;β、γ为描述Sigmoidal模型形状的参数),得到的拟合参数如表5所示.

表5 动态模量主曲线西格摩德模型Table 5 Sigmoidamodelof dynam icmodulusmaster curve

西格摩德模型的拟合结果表明回归模型对试验结果的拟合程度很高,试验结果对于模型的离散性很小,模型拟合效果良好.

4.2 试验结果变异性分析

对多个温度和频率下的半圆弯曲动态模量平行试验进行数据变异性分析有助于了解半圆弯曲试验方法的可靠性和数据离散的规律性,半圆弯曲动态模量的变异系数如表6所示.

由表 6可以看出,动态模量的变异系数绝大部分都在15%以内.变异系数较小,说明试验结果离散性和复现性偏差均较小,试验数据的准确性和精密度都控制得较好,试验结果真实可靠,一方面说明试验方法具有很好的稳定性,另一方面也说明采用来源一个圆柱体半圆试件可以减少数据的变异.从表6中还可以看出,在最大公称粒径为 20mm以下的数据的模量变异系数更小,最大公称粒径为 25mm的数据模量变异性稍大,说明集料的粒径大小对半圆弯曲动态模量的测试有一定的影响,因为微型变形引申计的测量范围为25.4mm,粒径的分布会影响测量的结果.

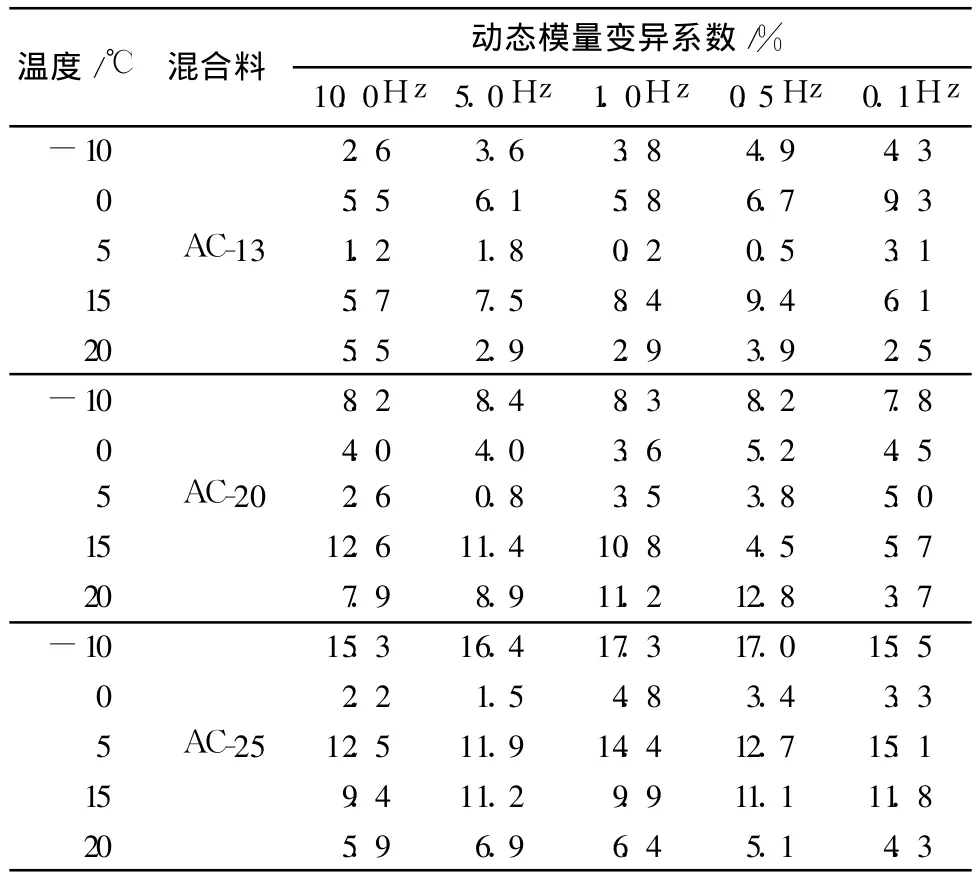
表6 半圆弯曲动态模量变异系数Table 6 Coefficient of variation of semi-circular bending dynamic modulus

沥青混合料的相位角由应力峰值与应变峰值的时间差结合频率进行计算,在系统加载时施加的偏正弦波并不是理想化的偏正弦波,从比荷载周期小1到 2个数量级的时间尺度来看,荷载是带杂波的,采集到的力的峰值与理想化的峰值并不重叠,同样应变的峰值也具有一定的波动性,这样就导致相位角的数据具有较大的离散性.无论是何种动态模量的测试方法都不可避免这样的问题,表 7为半圆弯曲动态模量测试时得到的相位角变异系数.

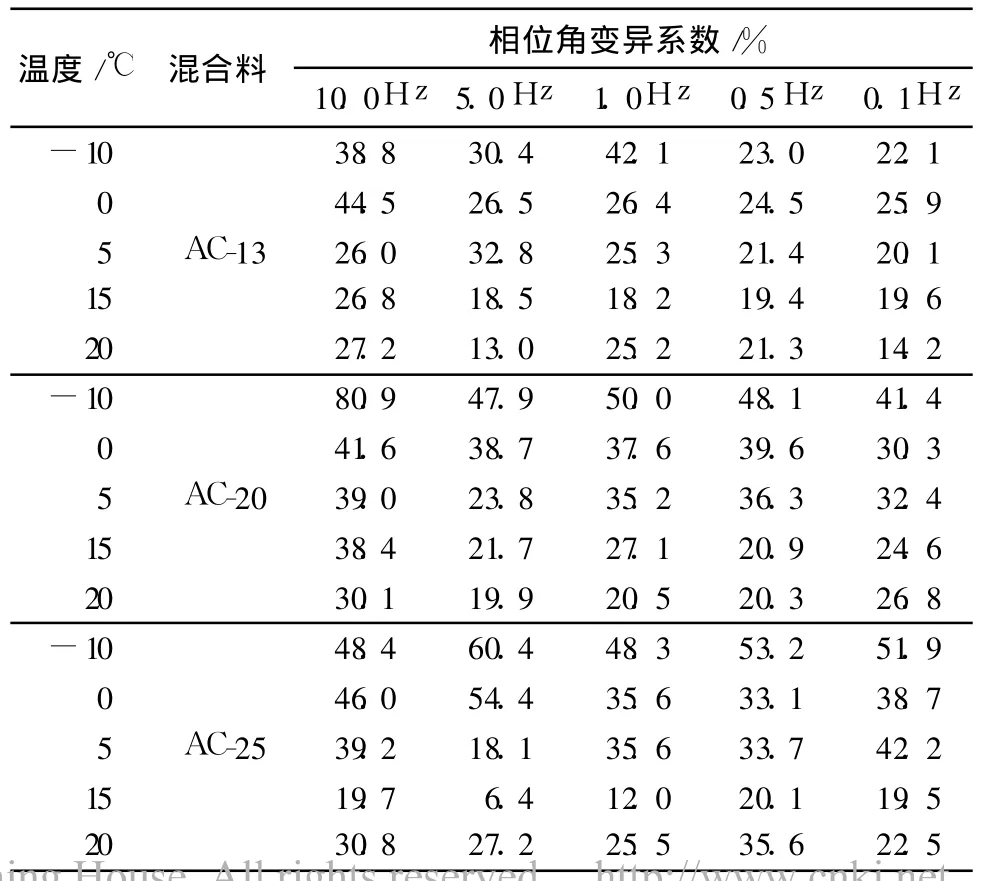
表7 相位角变异系数Table 7 Coefficientof variation of phase angle

可见,相位角相对动态模量来讲,变异系数明显偏大,随着粒径增大,相位角变异系数增大;同一温度下,当频率降低时,相位角增大,相位角变异系数变小.

5 结论

文中基于半圆试件开发了弯拉动态模量测试方法,对常用沥青面层沥青混合料进行动态模量测试,得到以下结论:(1)在分析半圆弯曲试验的荷载响应的基础上,开发了半圆弯曲动态模量测试方法,确定了试验参数.(2)开发的半圆试件测试动态模量可以为基于路面芯样的路面质量对设计的符合性检验建立可行的试验方法,通过三维有限元方法确立的应力系数有很好的精度,得到的弯拉动态模量符合精度要求,得到的动态模量主曲线与西格摩德模型符合得很好.(3)对试验数据的变异系数分析表明试验结果的离散性和复现性偏差均较小,说明试验方法具有很好的稳定性,动态模量的变异性会随着最大公称粒径的增大而稍有增加;相位角的变异性随着温度的增加或频率的降低而减小.

[1] 张肖宁.沥青混凝土路面施工的全面质量管理 [J].公路,2005,2:56-61.

Zhang Xiao-ning.Total quality management of construction of asphalt concrete pavements[J].Highway,2005, 2:56-61.

[2] Ayatollahi M R,Aliha M R M.Fracture parameters for cracked semi-circu lar specimen[J].J Rock Mech Min Sci,2004,41(3):1-5.

[3] Krans R L,Tolman F,Van de Ven M F C.Semi-circular bending test:a p ractical crack growth test using asphalt concrete cores[C]∥The 3th RILEM Con ference on Reflective Cranking in Pavements.Maastricht:[s.n.], 1996:331-342.

[4] Mull M A,Sturt K,Yehia A.Fracture resistance characterization of chemically modified crumb rubber asphalt pavement[J].Journal of Materials Science,2002,37: 557-566.

[5] Bayomy Fcuad,Abu Abdo Ahmad,Mull Mary Ann,et al. Evaluation of hotm ix asphalt(HMA)fracture resistance using the critical strain energy release rate[C]∥Jc Transportation Research Board 85th Annual Meeting. Washington D C:[s.n.],2006:9-14.

[6] Huang B,Zhang Z,Kingery W,et al.Fatigue crack characteristics of HMA mixtures containinng RAP[C]∥5th RILEM Conference on Cracking in Pavements-Mitigation, Risk Assessment and Prevention.France:[s.n.],2004: 631-637.

[7] Molenaar A A A,Scarpas A,Liu X,etal.Semi-circular bending test,simple butuseful[J].Journalof the Association of Asphalt Paving Technologists,2002,71(3):794-815.