隧道内列车着火的火焰顶棚射流温度特性研究*

毛军 郗艳红 樊洪明

(1.北京交通大学土木建筑工程学院,北京 100044;2.北京工业大学建筑工程学院,北京 100022)

列车发生火灾并停留在隧道内时,由于隧道顶棚较低,所以容易形成夹带火焰的顶棚射流.国内外有关烟气顶棚射流的研究较多,但对火焰顶棚射流的研究很少.例如,Alpert等[1-2]通过烟气羽流撞击顶棚实验得到了温度分布关系;Kurioka等[3]通过缩尺模型隧道实验提出了纵向风速下火源上方的最高温度预测模型;钟委[4]分析了地铁站台端部壁面对烟气顶棚射流最高温度的影响;Hu等[5-7]研究了烟气温度沿隧道顶棚的分布规律;王彦富等[8]研究了顶部开口半敞开式隧道在自然通风模式下的火灾特性.对于火焰顶棚射流,Hinkley等[9]研究了顶棚射流在走廊内蔓延的情况;毛军等[10]分析了列车中部着火时的火焰顶棚射流的温度特性.事实上,由于受火源位置和边界条件的影响,当火源位于列车的中部、头部或尾部时,顶棚射流特性会有所不同.研究隧道内列车着火时不同着火部位对火焰顶棚射流的温度特性的影响,有助于更好地给防火救援以指导.

1 列车头部和尾部着火的模型实验和数值模拟

由于客观条件的限制,难以在现场进行隧道列车火灾的全尺寸试验,因此,文中在1∶8几何缩尺的模型隧道内进行实验,再通过相似变换对原型进行研究.此模型比例尺可以保证与原型实验的相似性和精度.

(1)主要物理量的相似关系.

为了保证实验的相似性,还应满足运动相似、动力相似、热相似和边界条件相似.在隧道内列车火灾中,浮力效应起主导作用,火源附近的烟气流动为重力流;在机械通风的条件下,离火源较远处的气流是压力流,但由于雷诺数较大、容易进入阻力平方区,雷诺准则自动满足.因此,采用弗劳德准则作为相似准则.

弗劳德数:

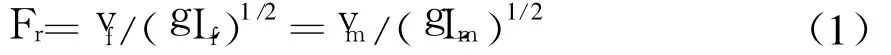
速度关系:

时间关系:

热相似准则采用无量纲量:

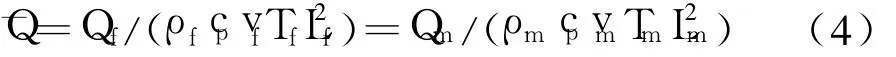
将式(2)代入式(3)得:

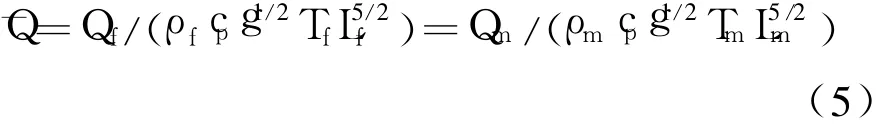
为了直接反映原型的温度变化规律,温度比例尺确定为1,即Tf=Tm,因此,热释放速率关系:

上式中:v为速度,m/s;g为重力加速度,m/s2;L为长度,m;Q为热释放速度,kW;ρ为密度,kg/m3;cp为定压比热,J/(kg◦K);T为温度,K;下标f代表原型;下标m代表模型.

(2)模型实验方法.

为了模拟实际列车的热释放速率和便于测量,采用液态庚烷作为燃料,燃料用量为 250mL,油面距离隧道顶面的高度为 200mm.由于地铁火灾的热释放速率一般为0～10MW,根据式(5)换算出本模型实验中的热释放速率应为 0～55 kW.油面距离隧道顶面的高度为 200mm,模型列车的尺寸为260mm×3000mm×350mm,相应的实验测点布置如图1所示.

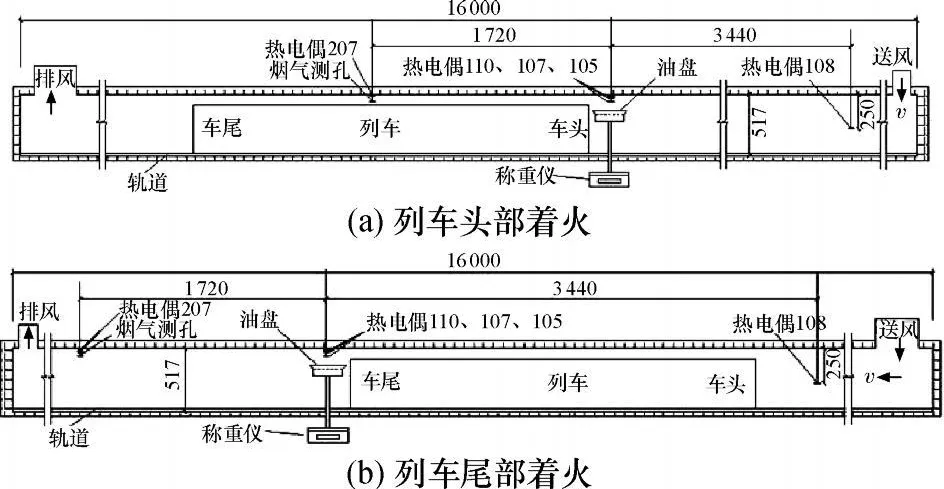
图1 地铁隧道模型的几何结构及测点布置图Fig.1 Geometric structure and layout ofmeasurement points in the subway tunnelmodel

采用质量损耗率法测定热释放速率:Q= φm˙ΔH.其中,φ为可燃物的燃烧效率,正庚烷燃烧充分时φ=93%[11];m˙为质量损失速率,将支承油盘的支架安装在电子天平上,对电子天平实时监测燃料质量随时间的变化情况;采样间隔为10s,燃烧时间为2～10min,由此换算得到m˙;ΔH为可燃物的热值,正庚烷的燃烧热值为48.24kJ/g.经过计算,燃料用量为250mL的庚烷,其热释放速率为38.66kW.隧道处于自然通风状态,风速近似为零.

图1中,编号分别为 110、107、105、108和 207的热电偶测点,离隧道顶的距离分别为 25、50、100、250和25mm,用于测量所在位置的温度.火源在装置中的相对位置未变,温度测点 110、107和 105始终位于火源的上方.将车厢移动到火源的左侧位置使火源位于列车的头部,相当于列车的头部着火,温度测点 207位于列车的上方;将车厢移动到火源的右侧位置使火源位于列车的尾部,相当于列车的尾部着火.

(3)数值模拟及其与模型实验的对比.

利用PHOENICS3.6软件,按实验模型中的相应尺寸和火源位置建模.采用带浮力修正的 k-ε两方程模型及有限容积法和SIMPLE算法,采用直角坐标系,计算域尺寸为556mm×8640mm×627mm,划分为 18200个网格,即加密火源处及环形空间处的网格.时间采用均步,每20.6s一步,共10步,内迭代次数为1500.

初始条件:假定在初始时刻(t=0)隧道内压强p=p0,速度分量u=0、v=0、w=0,温度θ=16℃,烟雾浓度C=0;在火源处,烟雾浓度C=5%;火源功率为38.66kW.

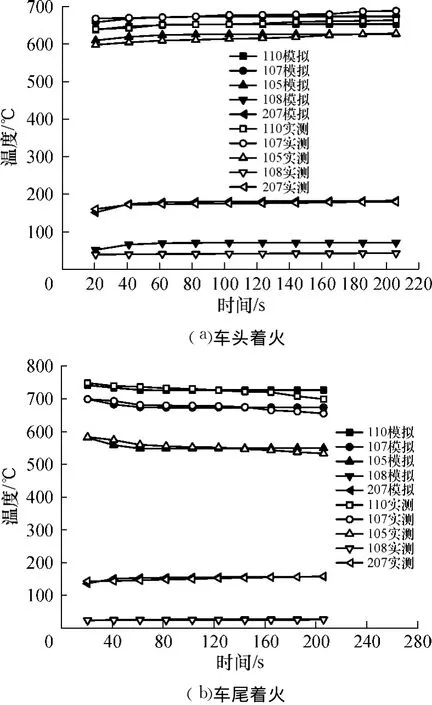
图2 实测与模拟温度对比Fig.2 Comparison ofnumerical and experimental temperatures

边界条件:隧道进口,给出速度条件,温度 θ= 16℃,烟雾浓度为 0;隧道出口,给出压力条件,出口边界使用充分发展条件,即在出口断面上的节点参数值对于出口边界内侧最邻近节点参数无影响.

隧道壁面:在隧道围护结构固体壁面及列车侧壁表面上,速度分量均采用无滑移边界条件.隧道及列车壁面均采用钢质材料,壁面函数采用对数壁面率,粗糙度均取为 0.013,辐射系数设为0.85.

考虑隧道内热辐射效应.烟气介质所含颗粒群的吸收和散射系数比气体大得多,可近似视为灰体,吸收系数为0.77,散射系数为 0.23,辐射换热模型选用IMMERSOL模型[12].

图2是温度的实测值与模拟值的对比情况.由图 2可见,绝大多数温度点的模型实验值与数值模拟值吻合较好,高温烟气层的温度尤为接近,只有个别低温区出现了较小的偏差,数值模拟结果是可信的.

2 列车头部和尾部着火时顶棚射流的温度特性

2.1 纵向温度时变规律

图3给出了风速为 0m/s的情况下,车头和车尾着火时的热释放速率时变曲线.由图 3可以看出,两者的变化趋势相近.燃烧初期,热释放速率逐步增大,在120 s左右达到最大;随着燃料的减少,热释放速率逐步减小.在相同的燃烧时间内,车头和车尾着火时的平均热释放速率近似相等,约为38.66kW.图4(a)、(b)分别为车头和车尾着火时的温度时变曲线.火源中心线位置的温度远高于其它纵向位置的温度.无论是车头还是车尾着火,各测点的温度时变曲线的变化趋势基本相同.在燃烧初期,火焰上方的温度在较短的时间内达到最高值,火焰和列车周围的烟气温度均快速上升,远离火源位置的温度因传热的延迟而温升滞后,在该段时间内变化不大;燃烧一段时间后,即 120s左右时各处温度在热释放速率达到最高并维持至燃烧结束.车头、车尾和中部着火时的最高温度分别约为 650、750和 700℃[10].

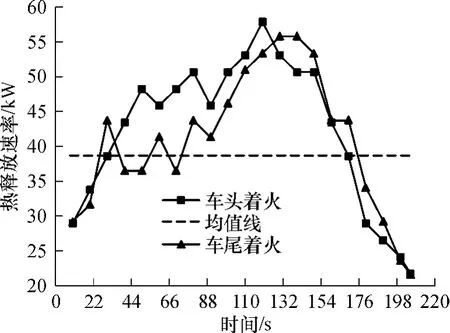
图3 热释放速率时变曲线Fig.3 Time-varying curve of heat release rate

图4 火源两侧位置温度时变曲线Fig.4 Temperature curves changing with time on both sides of the fire source

2.2 温度在隧道高度上的变化规律

与列车中部着火的情况相似,列车头部或尾部着火,火焰顶棚射流在高度方向上也产生温度变化.

图5(a)、(b)分别给出了隧道及列车与隧道顶的空间在高度方向上的火焰顶棚射流的温度分布情况.显然,由于壁面吸热,最高温度也不是出现在隧道顶壁,而是出现在离隧道顶较小的距离内.对于列车头部、尾部着火的情况,最大温度出现在距隧道顶 δ= 50mm的位置,燃料液面距离隧道顶H=200mm, δ=0.25H.这与纯烟气顶棚射流的最高温度出现在δ≤0.01H区域内的情况不同,与中部着火的最高温度出现在δ=0.18H也不同.此外,火源上方充满高温烟气,而在低于火源面的高度以下,烟气温度迅速降低.离开火源中心线一定距离后,热烟气层的厚度逐步稳定.火焰沿车长方向的列车顶部扩展,但其宽度小于隧道宽度,因此烟气层厚度等于列车顶部到隧道顶部的高度;离开列车后,烟气层的厚度变大,温度逐步下降.

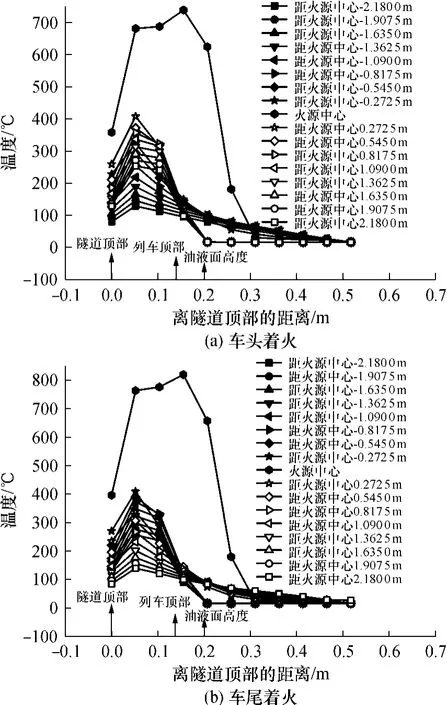
图5 火源中心线处温度随离开隧道顶部的距离变化曲线Fig.5 Temperature curves changing with different distances from the tunnel ceiling in the center line of fire

2.3 最高温度的纵向变化规律

图6(a)、(b)是火源中心线两侧最高温度随纵向距离衰减的情况,无论是头部还是尾部着火,在燃烧82.4s后纵向温度稳定下来,不再随时间变化.对其后燃烧时间内的温度曲线进行平均,并分成左右两段,以火源中心线为原点对平均曲线进行拟合,得到不同时刻的火焰顶棚射流最高温度的纵向变化规律,如图7所示.由图 7可知,在火源中心线附近温度产生突变,离开中心线一定距离后(图中±0.28m以内),纵向温度变化较为平缓,并呈抛物线规律.各时间段的对称轴非常接近,不同的是顶点值.而由文献[10]中可知,中部着火的纵向温度呈线性规律平缓变化,并且各时间段的斜率非常接近,不同的是温度坐标轴上截距值.

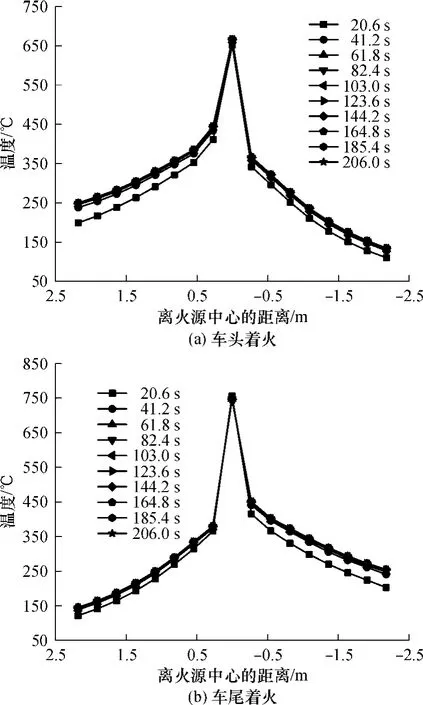
图6 火源两侧纵向的最高温度时变规律Fig.6 Maximum temperature curves changing with time in different distances from the fire source

回归曲线的相关系数 R用于检验回归方程是否符合变量变化的规律和判断回归方程的精度,若值接近 1,说明实测数据点都在回归曲线上,公式可靠,若值接近0,则所得的公式无意义.计算表明,在20.6、41.2、61.8 s时刻以及82.4～206.0 s的时间段平均的回归曲线中的相关系数均超过0.99,接近 1,故可认为此公式是可靠的.

由相似理论原理,将模型实验和数值模拟得到的数据换算到原型隧道,即可得到原型隧道列车着火的温度纵向衰减规律.

式中:Θ为隧道原型中摄氏温度;为时间;Y为原型隧道纵向坐标;B()、K()、A()为原型隧道中与时间有关的系数.数据见表2.

图7 最高温度对时间的平均值随离开火源中心距离变化的拟合曲线Fig.7 Maximum temperature fitting curves changing with differentdistances from the center line of fire

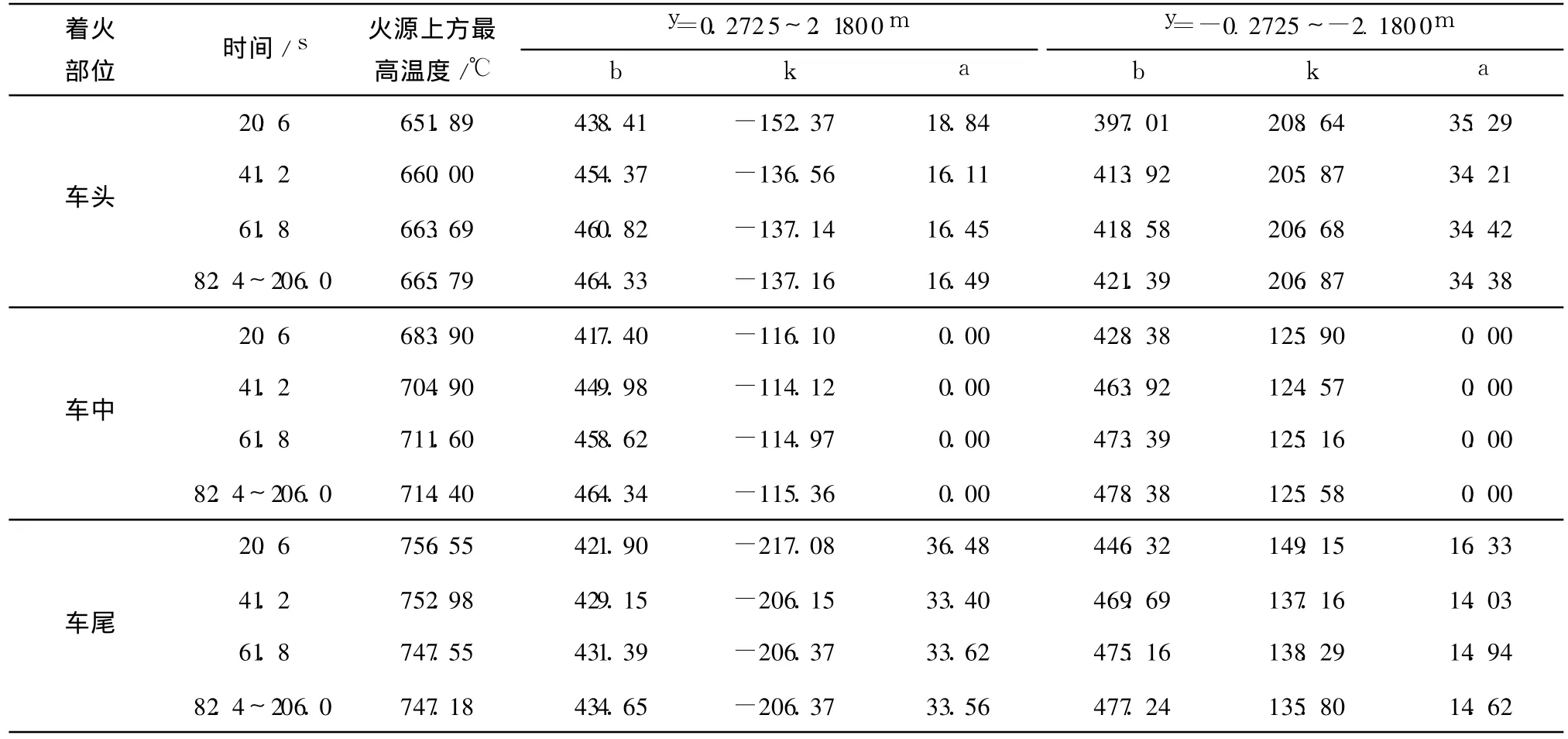
表1 模型中火焰顶棚射流温度的纵向衰减曲线系数(自然通风)Tab le 1 Coefficientof temperature vertical attenuation curve in flame ceiling jet(natural ventilation)-model

表2 原型中火焰顶棚射流温度的纵向衰减曲线系数(自然通风)Table 2 Coefficient of temperature vertical attenuation curve in flame ceiling jet(natural ventilation)-p rototype

由图 7及文献[10]可知,隧道内的地铁列车着火时,火焰顶棚射流的最高温度沿隧道的纵向衰减规律与一般隧道火灾纯烟气的温度衰减规律不同.后者是指数衰减规律,而前者在列车与隧道顶部空间以及列车首尾附近呈抛物线或直线衰减形式,且衰减速率不随时间变化;离开列车一定纵向距离后,不夹带火焰的烟气温度又呈指数形式变化,且温度梯度大于直线衰减的梯度.此外,无论车头还是车尾着火,其沿纵向的最高温度都不是关于火源中心线的对称分布形式.同样地,不论是车头、车中还是车尾着火,火源上方温度均产生突降.

图8(a)为纵向火源中心立剖面和隧道侧壁附近立剖面上的温度纵向变化曲线,Z为隧道宽度.由图可知:列车的头部或尾部着火时,火源附近的温度分布极不均匀,存在突变;不同的横断面和纵向断面的最高温度相差非常大,最大可达 400℃以上,隧道内的纵向温度分布也不再具有对称性.火源的无列车一侧的温度下降梯度明显大于有列车一侧的温度下降梯度.纵向火源中心立剖面上的温度衰减规律与隧道侧壁附近立剖面上的温度衰减规律在夹带火焰的顶棚射流区域内(有列车一侧)有所不同:前者在温度突降之后以抛物线规律衰减,而后者以指数规律衰减;但它们在纯烟气流动区域(无列车一侧的隧道)内的温度衰减规律则相同,都是以指数规律衰减,说明烟气在无列车的隧道内横向混合得比较均匀.因此,列车头部或尾部着火时,在夹带火焰的顶棚射流中,温度纵向衰减有两种形式共存:火焰区的温度以抛物线规律衰减,而纯烟气区域的温度则以指数形式衰减.

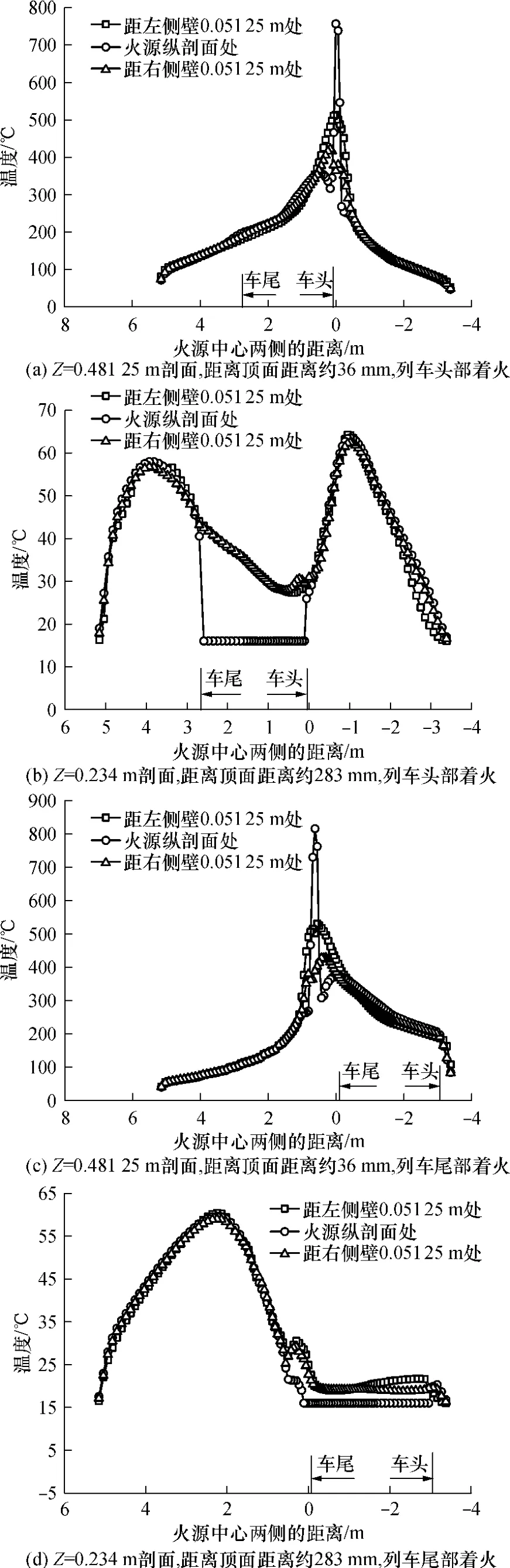
图8 不同高度上的温度随离开火源中心距离变化的情况Fig.8 Temperature curves changing with different distances from the center line of fire in different level

图8(b)、(d)所示的水平面距隧道顶面283mm,离隧道地面234mm,在列车上形成水平截面.在该高度,纵向中心立剖面的列车模型长度段的温度为常温(实际上不考虑列车模型的内部温度),所以温度分布在列车模型长度段内呈水平线,而在列车段之外与隧道侧壁附近纵向立剖面的温度分布规律相同.在隧道侧壁附近,以列车头部或尾部为基准,纯烟气的纵向温度由于热积累作用而逐渐升高;当烟气完全进入没有列车的区域时,其温度又因卷吸隧道内的冷空气而逐步下降.并且,在进入无列车的隧道区域后,隧道断面的温度分布均匀化.可见,顶棚射流的热烟气层未扩散到离隧道地面234mm高的以下区域,该高度以下区域的气体位于高温烟气层之外,主要受对流传热和部分热辐射的作用,最高温度不超过 65℃,因此,该区域内相对安全.根据几何相似,将模型隧道换算到实际隧道,对于列车着火的顶棚射流,该安全高度为 1872mm,低于该高度,烟气温度相对较低,相应的烟气浓度也较低;在火灾应急逃生和救援中,人员的行走高度只要低于 1.8m,安全逃生的机会较大.

4 结论

(1)列车头部、尾部着火时,火焰顶棚射流的最高温度出现在距隧道顶 δ=0.25H的位置,最高温度可达 800℃,中部着火时火焰顶棚射流的最高温度出现在δ=0.18H的位置,最高温度可达750℃以上;而纯烟气顶棚射流的最高温度出现在0.01H以内,相差较大;与列车中部着火的情况不同,列车车头和车尾着火的纵向温度变化不再以火源为中心对称分布,有列车一侧的纵向温度明显高于无列车一侧对应点的温度;

(2)无论列车头部、尾部着火,还是列车中部着火,火焰顶棚射流燃烧稳定后,温度沿隧道纵向变化的规律是分段的:前者在列车段及列车首尾附近的一定范围内,各断面的最高温度以抛物线规律衰减,后者则以线性规律衰减;离列车一定距离后,夹带火焰明显减少,二者的烟气顶棚射流最高温度都呈指数形式衰减;

(3)在夹带火焰的顶棚射流中,列车顶部的温度分布规律与隧道侧面附近的温度分布规律不同,存在两种形式的温度衰减方式:火焰区域的温度抛物线衰减规律和纯烟气区域的温度指数衰减规律;

(4)对于列车火灾形成的火焰顶棚射流,在一定的高度(这里为1.8m)以下,仍然存在温度较低的安全区域(低于 65℃)适合于人员疏散,而且列车另一端隧道内的烟气温度低于着火端隧道内的温度.

[1] Hasem i Y,Tokunaga T.Some experimentalaspects of turbu lent diffusion flames and buoyant p lumes from fire sources againsta wall out in a corner of walls[J].Combustion Science and Technology,1984(40):1-17.

[2] Alpert R.Ceiling-Jet Flows.In SFPE hand-book of fire protection engineering[M].[S.l.]:Natl Fire Protection Assu,1995:233-246.

[3] HitoshiKurioka,YasushiOkab,Hiroom iSatoha,etal.Fire properties in near field of square fire source with longitudinal ventilation in tunnels[J].Fire Safety Journal,2003 (38):319-340.

[4] 钟委.地铁站火灾烟气流动特性及控制方法研究[D].合肥:中国科学技术大学安全技术及工程学院, 2007.

[5] Hu LH,Huo R,Wang H B,etal.Experimental studies on fire-induced buoyant smoke temperature distribution along tunnel ceiling[J].Building and Environment,2007,42 (11):3905-3915.

[6] Hu L H,Huo R,Li Y Z,et al.Tracking a ceiling jet front for hot smoke tests in tunnels[J].Journal of Fire Sciences,2007,25(2):99-108.

[7] Hu L H,Huo R,Wang H B,etal.Experimental and numerical studies on longitudinal smoke temperature distribution upstream and downstream from the fire in a road tunnel [J].Journal of Fire Sciences,2007,25(1):23-43.

[8] 王彦富,龚延风,蒋军成,等.半敞开式隧道火灾实验[J].解放军理工大学学报:自然科学版,2008,9(3): 248-254.

Wang Yan-fu,Gong Yan-feng,Jiang Jun-cheng,et al.Fire testof tunnel with openings on roof[J].Journal of PLA University of Science and Technology:Natural Science Edition,2008,9(3):248-254.

[9] Hinkley P L,W raight H G H,Theobald C R.The contribution of flames under ceilings to fire spread in compartments[J].Fire Safety Journal,1984(7):227-242.

[10] 毛军,郗艳红,樊洪明.地铁隧道列车火灾的火焰顶棚射流温度特性研究 [J].土木工程学报,2010,43 (2):119-126.

Mao Jun,Xi Yan-hong,Fan Hong-m ing.Analysis of the characteristics of the flame ceiling jet temperature due to train fire in subway tunnels[J].China Civil Engineering Journal,2010,43(2):119-126.

[11] 范维澄,王清安,姜冯辉,等.火灾学简明教程 [M].合肥:中国科学技术大学出版社,1995:245-251.

[12] 王应时,范维澄,周力行,等.燃烧过程数值计算[M].北京:科学出版社,1986:176-201.