非线性油膜力作用下转子弯扭耦合振动特性研究

林海英

(北京航空航天大学 无人驾驶飞行器设计研究所,北京 100191)

崔 颖

(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)

非线性油膜力作用下转子弯扭耦合振动特性研究

林海英

(北京航空航天大学 无人驾驶飞行器设计研究所,北京 100191)

崔 颖

(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)

建立了非线性油膜力作用下转子-轴承系统弯扭耦合振动的数学模型.采用Rugge-Kutta数值积分方法计算模拟了转子升速过程中弯曲振动和扭转振动的不平衡响应,得到了转子弯曲振动的三维谱图和分岔图.分析发现,转子的弯曲振动会发生倍周期和概周期等复杂的非线性动力学行为.通过与不考虑弯扭耦合作用的系统特性进行比较,指出在转子弯曲振动临界转速附近,弯扭耦合作用对转子弯曲振动特性影响最大.数值分析揭示了扭转振动随转速升高,振幅基本保持不变,频率减小,有助于更深入地认识转子-轴承系统的弯扭耦合振动特性.

转子-轴承系统;弯扭耦合振动;非线性;不平衡响应

转子-轴承系统的振动特性是旋转机械领域研究的重点问题之一.在具有滑动轴承的转子系统中,在转子振动与润滑油流体运动相互耦合激励下转子在某些参数域内会发生油膜涡动甚至油膜振荡现象,这给转子的稳定运行造成严重影响.近年来,主要针对具有非线性油膜力的 Jeffcott转子模型的弯曲振动进行研究,揭示了一些复杂的非线性动力学行为特征[1-3].而实际转子的弯曲振动和扭转振动之间存在着相互耦合作用,这种耦合作用在一定条件下会对转子振动特性产生较大影响.文献[4]提出了利用弯扭耦合振动特性对旋转机械进行振动诊断的思想.文献[5-9]对转子弯扭耦合振动的研究仅限于对具有刚性支承或线性弹性支承的转子系统进行分析,还不能够对非线性油膜力作用下转子某些振动特性给出准确的解释.深入分析转子弯扭耦合振动特性,对于转子-轴承系统动力学设计和故障诊断技术的发展具有重要意义.

本文建立了考虑非线性油膜力的转子-轴承系统弯扭耦合振动数学模型,采用数值计算模拟转子的振动响应,得到了系统在一些参数域内的振动分岔图、三维谱图、时域波形、轴心轨迹等,直观显示了系统的弯扭耦合运动状态和特点,分析结果为采用滑动轴承转子系统的设计提供了一定的理论参考.

1 系统弯扭耦合振动模型的建立

1.1 转子-轴承系统的非线性动力学方程

以单盘柔性转子-轴承系统模型为研究对象,转子可简化为质量为 M2的轮盘与两个分布在轴承处质量为 M1的轴颈,它们之间由弯扭柔性的无质量轴连接,轴为各向同性,如图 1所示.转子支承在两个圆柱型滑动轴承上,作用在轴颈上的油膜力分量为 Fx,Fy.图 1中,O1为轴颈几何中心;O2为转子轮盘几何中心;M1为轴承处轴颈集中质量;M2为转子轮盘质量;c1为转子在轴承处结构阻尼;c2为转子轮盘阻尼;k为转轴弯曲刚度;kt为转轴扭转刚度.

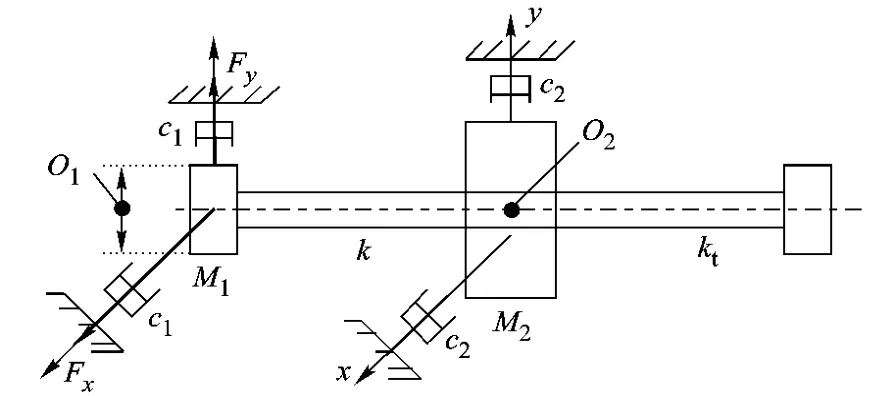
图1 转子-轴承系统模型示意图

设转子的旋转角速度为 Ω,Oc绕 O2的转角为 φ,θ为轮盘处扭转角位移,则有:

设 O1的坐标为(x1,y1),O2的坐标为(x2,y2).由于转子材料的不均匀、安转误差等原因,不平衡总是存在的,轮盘的不平衡偏心距为 e.

对轮盘作受力分析,得到轮盘弯曲振动微分方程:

轮盘的转动惯量为 J,对 O2点列力矩平衡方程式:

经整理,得轮盘扭转振动微分方程式为

轴颈弯曲振动微分方程:

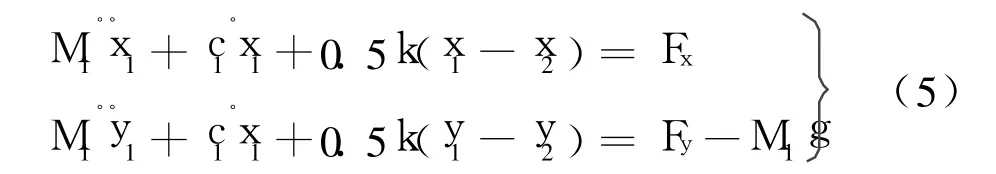
则单盘柔性转子弯扭耦合振动微分方程组为

1.2 非线性油膜力模型

文献[10]给出的非线性油膜力模型具有简洁明晰的解析表达式,并对转子-轴承系统动态响应特性的数值计算和分析具有较好的适用性.该油膜力模型的无量纲形式为

其中

2 数值计算结果及分析

对表 1中给定的系统参数,采用 Rugge-Kutta数值方法对式(6)进行求解,可计算出各种参数情况下转子弯曲振动和扭转振动的响应.

表 1 转子-轴承系统参数的取值

2.1 转子弯曲振动频率特性分析

对升速过程中转速区间内各转速下转子弯曲振动响应的时域计算结果进行 FFT分析,由三维频谱图可以得到转子弯曲振动的频率成分变化特征.如图 2所示,转子在低转速 200～360 rad/s区间内为工频振动;升高转速后系统出现 1/2倍频的成分,产生半速涡动,并且 1/2倍频成分的振动幅值随转速的增加而增大.在转速 510 rad/s时转子弯曲振动的频率除工频外不再是单一的 1/2倍频成分;进一步升高转速,系统出现 1/2,1/4和3/4倍频成分;转速升至转子弯曲振动一阶固有频率 707 rad/s附近时 1/2倍频成分的振动幅值减小;继续升高转速,系统的半速涡动间断地出现,并且半频成分的振动幅值逐渐增大.在非线性油膜力作用下考虑弯扭耦合作用,转子弯曲振动具有较为复杂的频率成分.

图2 轮盘弯曲振动三维谱图

2.2 转子弯曲振动分岔特性分析

Poincare截面是动力系统的流在状态空间中的横截超曲面.在前面建立的转子-轴承系统弯扭耦合振动的非自治系统方程中,Poincare截面上的一个点对应一个连续时间间隔为 T的时间点序列(T为激振力的周期).如果振动的周期为nT,Poincare映射为 n个离散的点.对于概周期运动,Poincare映射呈闭环结构.将转速作为分岔参数,绘制各个转速下的 Poincare截面,进而得到分岔图(图 3),可以分析转子的分岔特性.随转速的升高,系统的弯曲振动经历同步周期运动—倍周期—概周期运动—四倍周期—倍周期—概周期—倍周期—概周期一系列复杂的变化过程.通过与不考虑弯扭耦合作用的转子-轴承系统弯曲振动分岔图(图 4)相比较可见,由于弯扭耦合作用,在转子的一阶固有频率 707 rad/s附近转子的弯曲振动特性区别很大,转子的振动更加复杂.

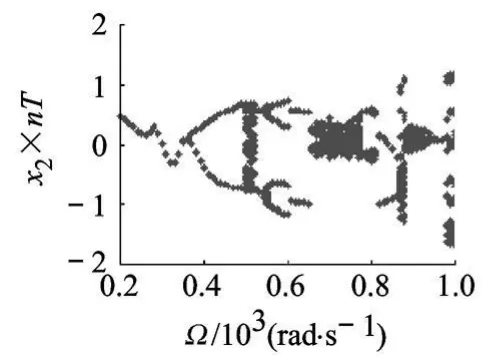
图3 考虑弯扭耦合轮盘弯曲振动的分岔图

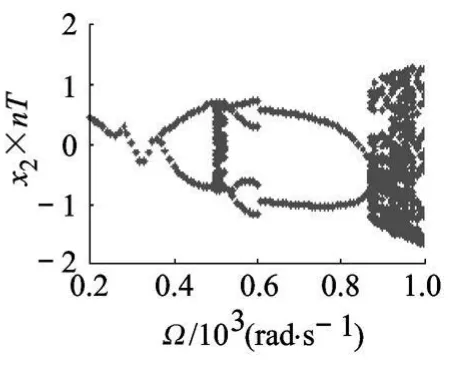
图4 不考虑弯扭耦合轮盘弯曲振动的分岔图

2.3 不同转速下转子弯曲和扭转振动运动分析

下面对几个典型转速下的转子弯曲振动和扭转振动的运动状态进行分析.图 5a为转速 Ω=265rad/s时转子的轴心轨迹,由图 3可见,在该转速下转子弯曲振动的 Poincare映射为单点,转子的弯曲振动频率与转速同步.图 5b为转速Ω=425 rad/s时的轴心轨迹,由图 2,该转速下转子振动出现转速的1/2倍频成分.由图 5c,在转速 Ω=510 rad/s下转子弯曲振动的频率成分中不再是转速的 1倍频和单一的 1/2倍频的叠加,而是在1/2倍频附近有多个频率成分.图 5d为转速 Ω=590rad/s时的轴心轨迹.由图 3可见,弯曲振动的Poincare映射为 4个单点,为四倍分岔运动.

该模型转子的一阶固有频率为 707 rad/s,在此转速附近区域,转子弯曲振动与扭转振动之间的耦合作用对系统的动力特性影响较大.图 6a为考虑弯扭耦合作用的情况下,转速 Ω=700 rad/s时转子的轴心轨迹,结合该转速下的频率成分分析(参见图 2),该转速下转子的低频分量含有多个频率成分.不考虑弯扭耦合作用的情况下,转速Ω=700 rad/s时转子弯曲振动的轴心轨迹如图 6b所示,该转速下 Poincare映射是两个单点的倍周期运动(参见图 4).通过比较图 6a与图 6b可知,转子-轴承系统在一阶固有频率附近弯扭耦合作用对转子弯曲振动特性的影响很大.

图5 在不同转速下轮盘的轴心轨迹

图6 转速Ω=700rad/s下轮盘的轴心轨迹

转子扭转振动的运动状态如图 7所示,图中给出了各个转速下扭转振动的时域波形,横坐标设为 τ=Ωt.在各个转速下,转子扭转振动的频率均远低于弯曲振动的频率;随着转速的升高,扭转振动的频率降低,而振幅基本不变.由于转子弯曲振动的频率成分与扭转振动的振幅、角频率有关,那么随着扭转振动角频率的降低,弯扭耦合作用在加强.

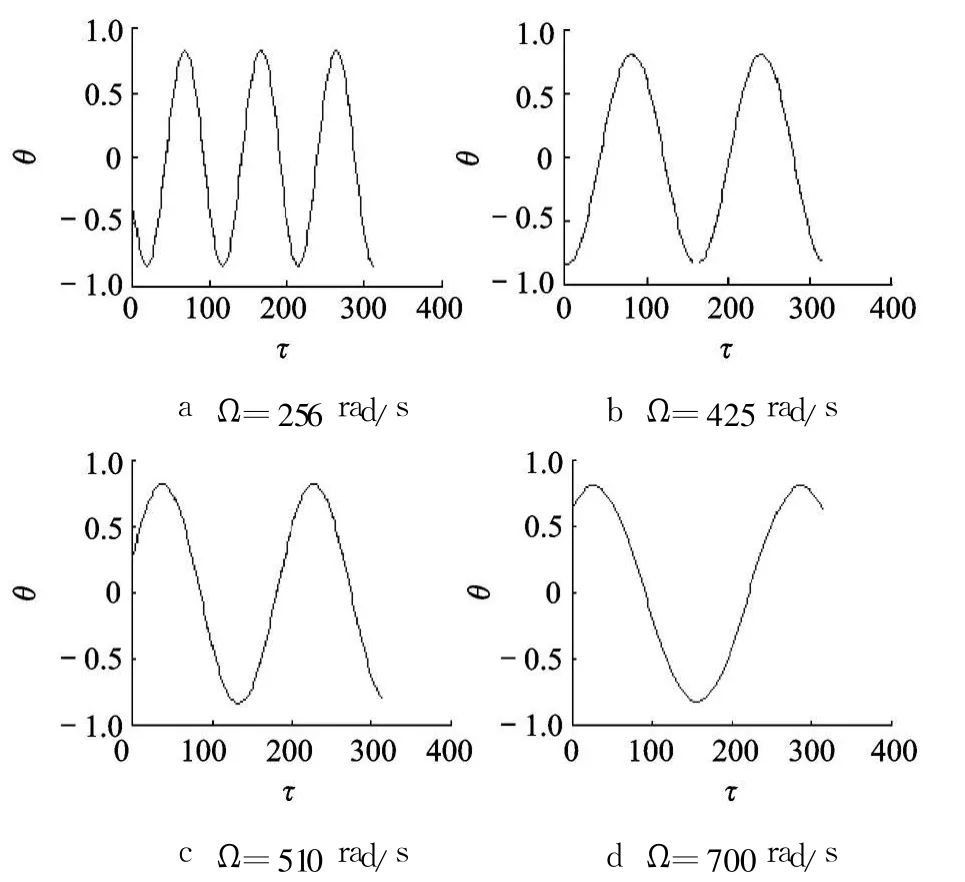
图7 转子扭转振动的时间历程

3 结 论

1)对于非线性油膜力作用下的转子-轴承系统,考虑弯扭耦合作用的情况下,系统有发生复杂非线性动力学行为(如倍周期、概周期运动、四倍周期)的可能.

2)转子-轴承系统的转速接近 1/2一阶固有频率时,系统开始产生半频涡动,调整系统参数,使系统出现此低频分量的转速不在工作转速区内,对转子的稳定运行具有重要的意义.在一阶固有频率附近区域,转子的弯扭耦合作用更加明显,对系统的运动状态影响最大.

3)随着转速的增大,考虑非线性油膜力的转子-轴承系统的扭转振动的频率随之降低,振幅变化不大,系统弯曲振动和扭转振动之间的耦合作用不断加强.

References)

[1]Adiletta G,Guido A R,Rossi C.Chaotic motions of a rigid rotor in short journalbearings[J].Nonlinear Dynamics,1996,10(3):251-269

[2]Wang JK,Khonsari M M.Application of hopf bifurcation theory to rotor-bearing system with consideration of turbulent effects[J].Tribology International,2006,39(7):701-714

[3]陈予恕,丁千,孟泉.非线性转子的低频振动失稳机理分析[J].应用力学学报,1998,15(1):113-117 Chen Yushu,Ding Qian,Meng Quan.Mechanism of subsynchronous vibration for a nonlinear rotor[J].Chinese Journal of Applied Mechanics,1998,15(1):113-117(in Chinese)

[4]Muszynska A.Vibration diagnostics of rotating machinery malfunctions[J].International Journal of Rotating Machinery,1995,1(3/4):237-266

[5]Kellenberger W B.Forced resonances in rotating shafts:the combined effects of bending and torsion[J].Brown Boveri Rev,1980,2:117-121

[6]Cohen R,Porat I.Coupled torsional and transverse vibration of unbalanced rotor[J].Journal of Applied Mechanics,1985,52(9):701-705

[7]Nataraj C.On the interaction of torsion and bending in rotating shafts[J].Journal of Applied Mechanics,1993,60(3):239-241

[8]Wong E.Dynamic response of a coupled spinning Timoshenko shaft system[J].Journal of V ibration and Acoustics,1999,121(1):110-113

[9]何成兵,顾煜炯,陈祖强.质量不平衡转子的弯扭耦合振动分析[J].中国电机工程学报,2006,26(14):134-139 He Chengbing,Gu Yujiong,Chen Zuqiang.Coupled flexural-torsion vibration of rotor with unbalance mass[J].Proceeding of the CSEE,2006,26(14):134-139(in Chinese)

[10]Capone G.Descizioneanalitica del campodiforze fluidodinamico neicuscinetticilindrici lubrificati[J].L'Energia Elettrica,1991,68(3):105-110

(编 辑 :李 晶)

On coupled bending and torsion of rotor w ith nonlinear oil-film force

Lin Haiying

(Research Institute of Unmanned Aerial Vehicle,Beijing University ofAeronauticsand Astronautics,Beijing 100191,China)

Cui Ying

(School of Energy Science and Engineering,Harbin Institute of Technology,Harbin 150001,China)

Am a thematic al model of a rotor with nonlinearoil-film force was presented,in which coup led bending and torsion were considered.The unbalance response of the rotor was numerically calculated by Rugge-Kutta method,and the bifurcation diagrams and waterfall plot were obtained to analyze dynamic characteristics of the system.The results revealemultiform complex nonlinear dynamic behavior of the rotor,that comprises periodic,double periodic and quasi-periodic motion.By comparing with dynamic characteristic of the system without considering the interaction of bending and torsion,its hows that bending vibration is heavily affected by the interaction of bending and torsion when rotating speed is near by the critical speed.The numerical study illustrated characteristics of torsion with increasing rotating speed.The results can provide a deeper understanding to coupled bending and torsion of the rotor-bearing system.

rotor-bearing system;coupled bending and torsion;nonlinear oil-film force;unbalance response

TH 212;TH 213.3

A

1001-5965(2010)05-0588-04

2010-01-28

航空科学基金资助项目(2008ZB51011)

林海英(1971-),男,吉林永吉人,工程师,haiying@buaa.edu.cn.