基于运动灵活性的蟑螂机器人机构参数优化

张建斌 宋荣贵 陈伟海 张广萍

(北京航空航天大学 机械工程及自动化学院,北京 100191)

基于运动灵活性的蟑螂机器人机构参数优化

张建斌 宋荣贵 陈伟海 张广萍

(北京航空航天大学 机械工程及自动化学院,北京 100191)

从仿生蟑螂机器人机构特点出发,基于运动灵活性,选择椭圆形身体布局,分别以单腿工作空间和整机雅克比矩阵的条件数倒数作为灵巧度指标,在兼顾运动灵活性和可靠性的基础上,对机器人机构参数进行优化配置,选择了最优的杆长比例.利用分析得出的优化尺寸建立 ADAMS参数化仿真模型进行实验研究,仿真结果与理论分析相吻合,验证了优化配置的可行性和正确性,为样机的研制和机器人的驱动及控制等进一步研究奠定了基础,也为其他六足机器人的开发提供了参考.

仿生蟑螂机器人;灵活性;优化;雅克比矩阵

仿生蟑螂机器人是基于蟑螂运动灵活稳定,对地形适应能力强等优点而开发的并联运动机构,通常采用三角步态行进[1],具有较好的机动性,对不平路面适应能力突出,可以轻松跨过较大障碍物.因此在抗震救灾、搜索救援、外星探索等领域有着广泛的应用[2].

从机构学角度看,仿生蟑螂是一个复杂的冗余驱动多支链并联机构,优化配置其机构参数,提高运动灵活性和稳定性极其重要,目前主要是采用工作空间和灵巧度进行优化[3-5].

工作空间是机器人的操作区域,是机器人运动性能的重要指标.而灵巧度则可以认为是表征机器人自主改变其位姿或方向以及传递力和力矩的能力[6],常用雅克比矩阵条件数和可操作度[2-3]表示.

国内外许多学者基于雅克比矩阵条件数、工作空间以及全局灵巧度指标[4]对多种机器人进行了研究[7-10].采用工作空间和基于雅克比矩阵的灵巧度指标,对机器人的结构参数进行优化配置,其结果更加可靠和准确,在体现运动灵活性的基础上,保证了运动的准确和可靠性,同时也可以使机器人尽量远离奇异空间.

本文从仿生蟑螂机器人的机构学特点出发,基于运动灵活性,分别以单腿工作空间和整机雅克比矩阵的条件数倒数作为灵巧度指标,对其机构参数进行优化配置.利用分析得出的优化尺寸建立了参数化模型进行仿真研究,验证了优化配置的可行性和正确性,为样机的研制铺平了道路,也为其他六足机器人的开发提供了参考.

1 蟑螂机器人机体结构

蟑螂有 6条腿,对称式分布,一般研究常用的机器蟑螂结构如图 1a所示.机体成长方形,六足对称分布,每条腿有 4个关节,分别为髋关节、大腿、小腿和踝关节,其中前 3个关节为驱动关节,各关节之间的连杆分别称为基节、股节和胫节.

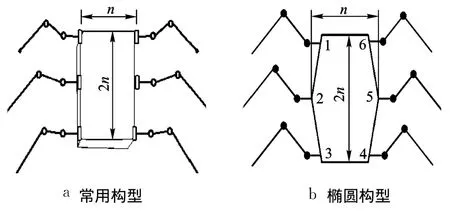
图1 蟑螂机器人机构简图

实际蟑螂及大多数昆虫的身体都不是长方形,而是呈椭圆形[11],后者运动性能更好.

图2为等长宽比、不同结构的髋关节摆动范围及支撑三角形,阴影部分表示髋关节可达到的转角范围.图 3为支撑三角形对比,DE与 D′E′为表征机器人运动稳定性的重要指标[12]:纵向稳定裕量 SL.可以看出,椭圆形布局减少了腿的碰撞,增大了髋关节转动范围,提高了运动灵活性;同时明显增大了纵向稳定裕量,提高了机器人的运动稳定性.因此,本研究中的仿生蟑螂机器人采用椭圆型的身体结构.

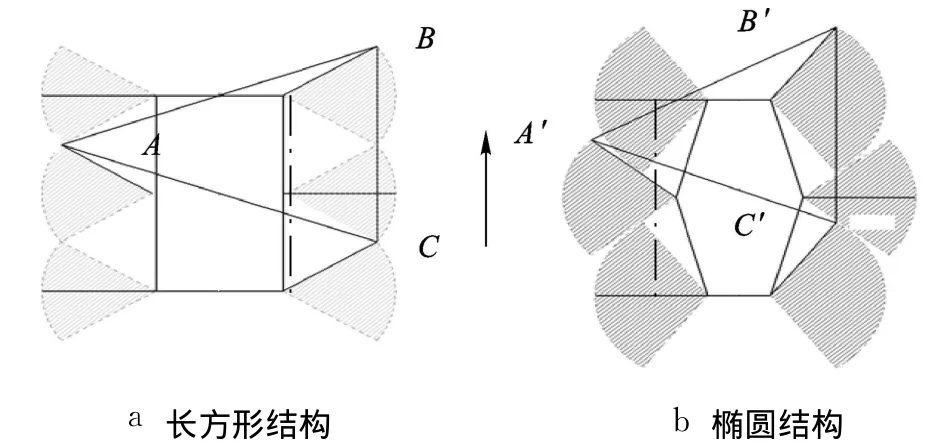
图2 两种结构髋关节摆角及支撑三角形

图3 支撑三角形对比

2 基于单腿工作空间的参数优化

机器人摆动腿可视为串联机械臂,其足端所能到达的工作空间可以参照机械臂工作空间求得,并作为衡量机器人运动能力的重要指标.

2.1 仿生蟑螂步行足工作空间求解

蟑螂机器人足端工作空间就是机器人足端在机构限制下所能达到的空间点的集合,决定了机器人所能选择的立足点范围.工作空间越大,机器人末端操作空间越大,步行足的灵活性也越大.

应用蒙特卡洛法随机选取关节空间变量组合,然后根据机器人正向运动学计算出足端坐标,这些坐标值的集合就形成了机器人足端的工作空间[13].

取机器人一条腿为研究对象,根据 D-H法建立坐标系,如图 4所示,表 1为其 D-H参数.

图4 步行足 D-H坐标系示意图

表 1 步行足D-H参数表

由机器人前向运动学可知,步行足末端 A在固定坐标系 O-xyz中的坐标为

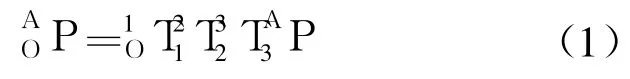
在各个关节变量的变化范围内,随机生成 n组关节变量的组合,由式(1)求出其固定坐标值,将 n组点同时显示出来,就形成了机器人步行足摆动腿的工作空间点云图.

图5所示为采用 30 000个随机点,取 L1=50mm,L2=100mm,L3=200mm时步行足工作空间点云图及其在 xy平面的投影.

图5 摆动步行足工作空间及其 xy面投影

2.2 工作空间大小与关节长度的关系

机器蟑螂单腿工作空间的体积大小,直接决定了其躲避障碍和选择立足点的空间大小.在各个关节转角范围一定的情况下,各个关节杆的长度比例是影响工作空间大小的主要因素.因此以工作空间体积大小为目标合理配置关节杆长.

2.2.1 工作空间大小计算

工作空间点云图显示了工作空间的形状,所得到的是一系列离散的数据点.其体积大小则需要根据这些离散点,采用微积分的思想求出[12].

具体步骤如下:1)沿 z向,将工作空间等分为 n块平面片;2)对每个平面片,沿 x方向再次等分为 m个矩形条,用每个矩形条的面积和来近似实际面积;

3)求和得出每个平面片的面积,与 z向间距相乘后再求和,即可得出工作空间的近似体积.

对于可能存在的空洞,需要进行判断:将 x方向等分的 m个矩形长条中的 y坐标进行排序,然后判断相邻的两个值是否相差很大,例如若超过等分间距的 3倍,即视为空洞,加以剔除.

2.2.2 工作空间大小与关节长度比例的关系

随着各个关节杆长度比例的不同,机器人步行足工作空间大小在不断变化,因此,需要选择合理的长度比例配置,满足工作空间最大的原则.

设机器人的单腿长度为 350mm,其中基节比例为 μ1,股节比例为 μ2,胫节则为 1-μ1-μ2.取μ1∈ [0,0.4],μ2∈ [0,0.6],编程计算关节比例和工作空间体积的关系,结果如图 6所示.

图6 关节比例与工作空间体积关系

可以看出,基节比例在[0,0.1]之间,股节比例在[0,0.3]之间时,工作空间体积较大,此时单腿的灵活性较高.机器人可以在较大的工作空间内自主选择立足点,从而可以更加灵活地适应各种复杂的路面情况.

3 基于躯体灵巧度的参数优化

蟑螂机器人处于站立或者采用三角步态行走时,其躯体从机构学角度看,分别是一个由 6条、3条支撑腿组成的复合多变的多支链闭环并联机构.

运动机构应该远离奇异形位.当机器人接近奇异形位时,其雅克比矩阵为病态矩阵,逆矩阵精度降低,从而使输入和输出运动间的传递失真.

灵巧度就是衡量这种失真程度的指标,目前对于灵巧性的考察,主要有雅克比矩阵条件数、可操作度等指标.矩阵的条件数定量的表示矩阵求逆的精度和稳定性,因此本文用矩阵条件数来表示机器人的灵巧性.

3.1 仿生蟑螂机体雅克比矩阵

对于仿生蟑螂这样的多支链并联机构,首先要研究其单腿的雅克比矩阵[14-15],建立相应的坐标系,如图 7所示.

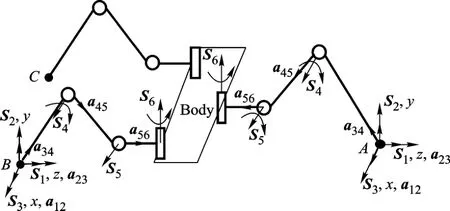
图7 仿生蟑螂步行足相关坐标系

从机体开始,单腿依次由一个球关节(与地接触)和 3个转动关节组成.球关节可以看成图 8所示的 3个串联转动关节的组合.

图8 球关节简化为旋转关节

主运动副轴线用单位矢量Si表示,相邻轴线间公法线为单位矢量 a12,a23,…,aij,公法线间沿Si的偏距为 Si,公法线长度为 aij,公法线间转角为 θj,坐标系间转角为 αij.

机器人单腿分支关节角与仿生蟑螂机体之间的关系见下式:

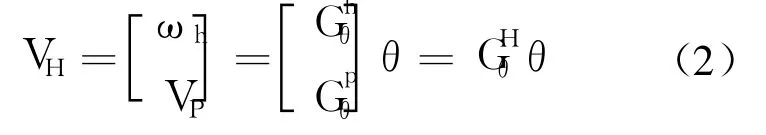
其中

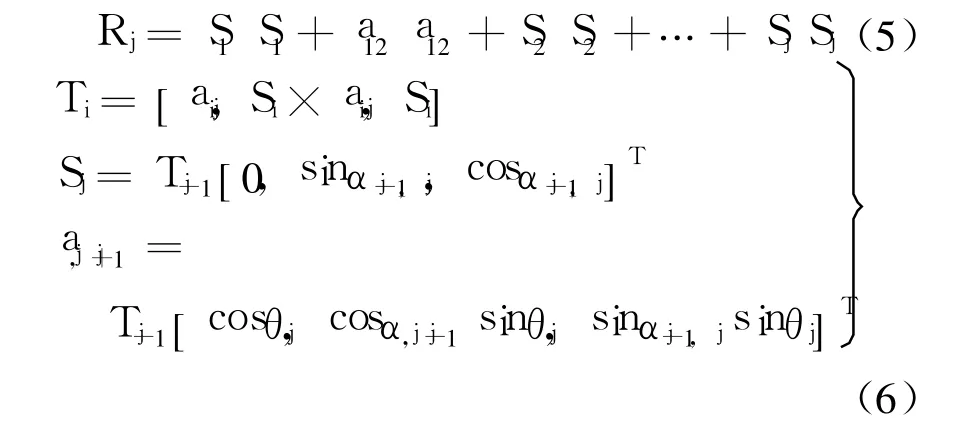
P为机体重心在分支腿末端坐标系中的坐标,根据几何关系和各个关节杆的长度,向末端坐标系进行投影可以获得.初始时:S1=[0,0,1]T,a12=[cosθ1,sinθ1,0]T.

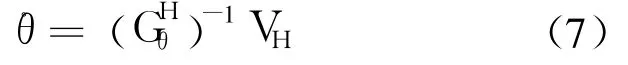
蟑螂机器人通常采用三角步态行走,有三条支撑腿,不妨取 1,3,5腿.在此位姿下,这 3个分支腿与机体的运动关系分别为

蟑螂机器人各分支中只有 4,5,6关节为主动关节,因此,取出上面各矩阵的 4,5,6行组成:

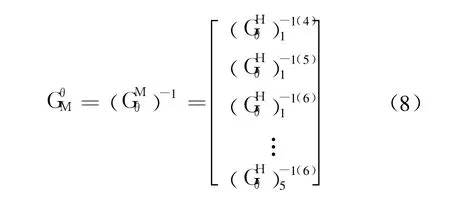
3.2 基于灵巧度的机构参数优化

表 2为采用三足支撑爬行状态下仿生蟑螂1,3,5腿的相关参数.

表 2 仿生蟑螂支撑腿坐标系相关参数

由式(2)～式(9)可计算出此位姿下机器人的雅克比矩阵.在固定的形位下,雅克比矩阵及其条件数和机器人的机构尺寸关系紧密.因此,以雅克比矩阵的条件数倒数为灵巧度指标优化关节参数.

采用 Frobenius范数计算雅克比矩阵条件数,G表示雅克比矩阵,则灵巧度指标为

根据不同的关节长度比例配置,以 η∈[0,1]为指标,在 MATLAB中编程计算出关节杆长和灵巧度的关系如图 9所示.

图9 灵巧度与关节长度比例关系

可以看出,当基节比例在[0,0.1]之间,股节比例在[0.3,0.6]之间时,机器人灵巧度较大,接近奇异形位时,输入和输出之间的误差最小,机器人可以稳定可靠地执行运动命令,整机运动性能较高且灵活可靠.

综合可知,采用椭圆对称型身体结构,基节杆长取为单腿总长的 0.05,股节比例取为 0.3,胫节比例为 0.65,蟑螂机器人单腿和整机的运动灵活性和可靠性都比较好,机器人可以在较大的范围内适应复杂路面情况,灵活选择合适的立足点,同时能保证较高的运动精度和可靠性.

4 仿真研究

利用 ADAMS参数化建模和评估功能,建立仿生蟑螂机器人的参数化模型,通过试验设计(DOE,Design Of Experiments)的方法同时研究基节和股节比例变化对机器人整体的影响.

采用文献[9]提出的评价指标灵活度 F作为试验设计的评价目标.

式中,Sx,Sy,Sz和 φx,φy,φz分别表示机器人沿 x,y,z 3个方向所能移动和转动的最大范围.

参照文献[11],利用 ADAMS建立机器人参数化模型,见图 10.将基节和股节的比例设置为参变量,以 F最大化为目标进行 DOE计算,计算结果图 11.基节比例范围取[0.01,0.2],股节比例范围取[0.3,0.5].

图10 ADAMS中仿生蟑螂机器人参数化模型

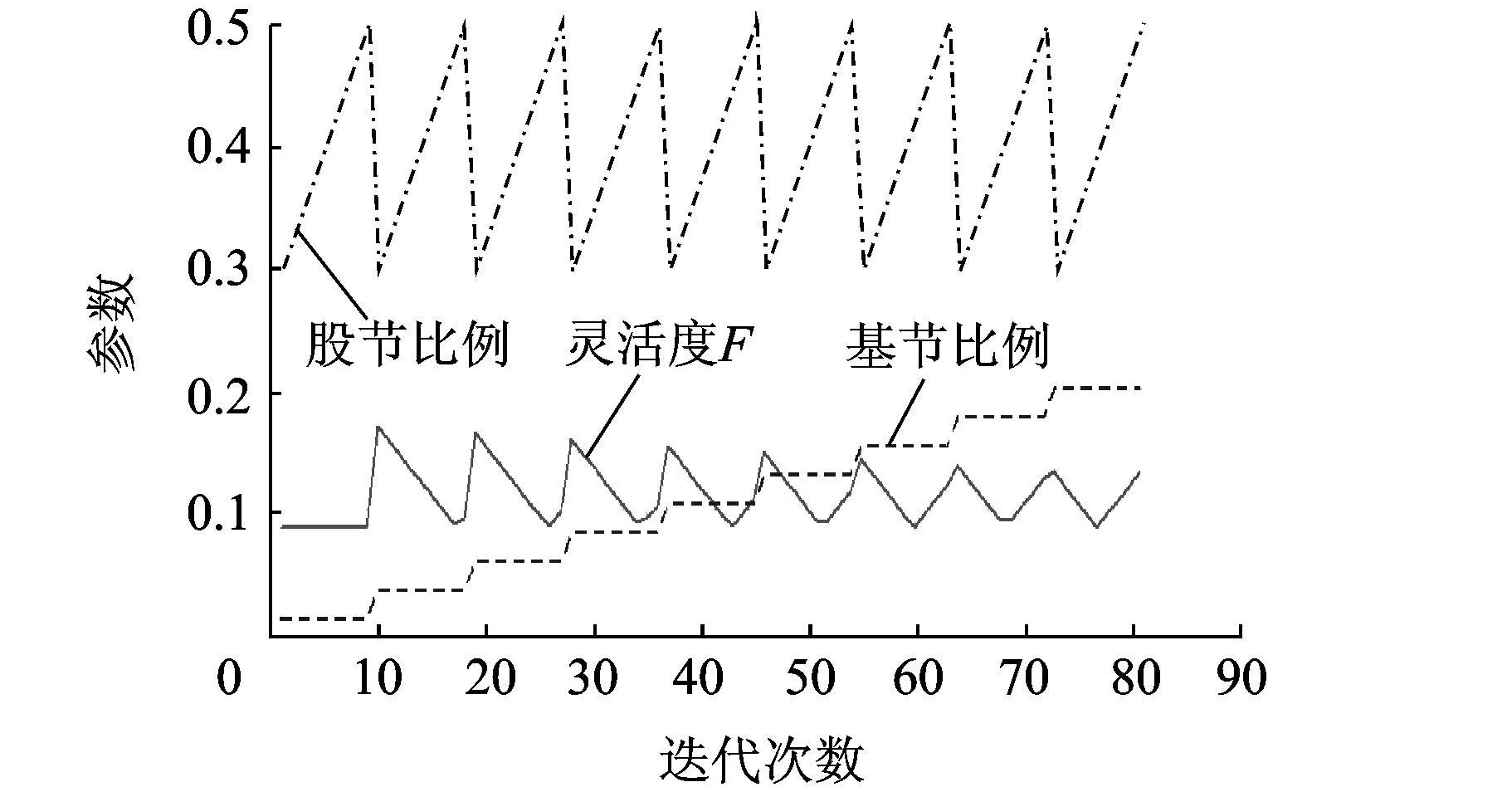
图11 ADAMS试验设计结果

可以看出,当基节比例较小时 (图 11中0.01～0.045),由于容易发生干涉,F较小;当基节比例为 0.045,股节比例为 0.3时,F最大,表明此时机器人机体所能运动的范围和运动能力最大;之后随着基节和股节比例的增大,F减小.

仿真结果表明:在不影响整机布置和装配关系时,取基节比例 0.045,股节比例 0.3时,机器人具有较好的运动能力和灵活性.这与理论分析中所取的基节比例 0.05和股节比例 0.3相一致,从而验证了理论分析的正确性和可行性.

5 结 论

本文从仿生蟑螂机器人的机构学特点出发,选择采用椭圆形身体布局,基于运动灵活性分别以单腿的工作空间和整机的雅克比矩阵条件数倒数作为灵巧度目标,对其机构参数进行优化,确定了各个关节杆长的最优配置.并通过 ADASMS仿真模型,进行了试验设计,结果表明优化后的机器人运动性能良好,运动灵活,与理论分析吻合,验证了优化配置的可行性和正确性,为其他六足机器人的驱动和控制等进一步研究奠定了基础.

References)

[1]Bai Shaoping,Low K H,Guo Weimiao.Kinematographic experimentson legmovements and body trajectoriesof cockroach walking on diffent terrain[C]//Proc of IEEE Inter Conf on Robotics and Automation.San Francisco:IEEE,2000:2605-2610

[2]Chen Weihai,Yang Guilin,Ho E H L,et al.Interactive motion controlofmodular reconfigurablemanipulators[C]//Inter Conf on Intelligent Robots and Systems.Las Vegas:IEEE,2003:1620-1625

[3]Gosselin CM,Angeles J.The optimum kinematic design ofa planar 3-DOF parallelmanipulators[J].ASME Journal of Mechanical Design,1998,110(1):35-40

[4]Gosselin C M,Angeles J.A global performance index for the kinematic optimization of robotic manipulators[J].ASME Journal of Mechanical Design,1991,113(3):220-226

[5]Kumar V.Characterization of workspacesofparallelmanipulators[J].ASME Journalof Mechanical Design,1992,114(3):368-375

[6]Xu Qingsong,Li Yangmin.K inematic analysis and optimization of a new compliant parallel Micromanipulator[J].Inter Journal of Advanced Robotic Systems,2006,3(4):351-358

[7]Kircanski M.Kinematic isotropy and optimal kinematic design of planar manipulators and a 3-DOF spatial manipulator[J].International Journal of Robotic Research,1996,15(1):61-77

[8]唐粲,贠超,栾胜.一种新型医疗机器人运动学及灵活性分析[J].北京航空航天大学学报,2005,31(7):748-752 Tang Can,Yun Chao,Luan Sheng.Analysis of kinematics and dexterity for new surgery robot[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(7):748-752(in Chinese)

[9]赵铁石,赵永生,黄真.仿蟹步行机构模型灵活度分析 [J].中国机械工程,1998,9(3):52-54 Zhao Tieshi,Zhao Yongsheng,Huang Zhen.The flexibility of walking machine imitating a crab[J].China Mechanical Engineering,1998,9(3):52-54(in Chinese)

[10]韩宝玲,王秋丽,罗庆生.六足仿生步行机器人足端工作空间和灵活度研究 [J].机械设计与研究,2006,22(4):10-12 Han Baoling,Wang Qiuli,Luo Qingsheng.Mechanical optimization and analyses of hex apod walking bio-robot[J].Machine Design and Research,2006,22(4):10-12(in Chinese)

[11]罗庆生,韩宝玲.现代仿生机器人设计[M].北京:电子工业出版社,2008:48-60 Luo Qingsheng,Han Baoling.The design ofmodern bionic robot[M].Beijing:Publish House of Electronics Industry,2008:48-60(in Chinese)

[12]曹毅.显微外科手术机器人工作空间分析与综合[D].天津:天津大学机械工程学院,2004 Cao Yi.Workspace analysisand synthesis ofmicrosurgical robot[D].Tianjing:School ofMechanical Engineering,TianjingUniversity,2004(in Chinese)

[13]张明.机器人工作空间仿真研究 [J].现代机械,2000(4):38-39 Zhang Ming.The simulation research of robot workspace[J].Modern Machinery,2000(4):38-39(in Chinese)

[14]黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997:91-103 Huang Zhen,Kong Lingfu,Fang Yuefa.Theory and control of mechanism for parallel robotics[M].Beijing:China Machine Press,1997:91-108(in Chinese)

[15]孙磊.仿生机器蟹原理样机的研究[D].哈尔滨:哈尔滨工程大学机电工程学院,2005 Sun Lei.Research on theprototype of crab-like robot[D].Harbin:College of Mechanical and Electrical Engineering,Harbin Engineering University,2005(in Chinese)

(编 辑 :李 晶)

Mechanism optimization of bionic cock roach robot based on locomotion dexterity

Zhang Jianbin Song Ronggui Chen Weihai Zhang Guangping

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The oval body con figuration based on the characteristic of mechanism and the locomotion dexterity ofa bionic cockroach robot was chosen.The workspace of a single leg and the dexterity denoted by the reciprocal of condition number of the whole body's Jacobian matrix were used to optimize and configure the parameters of mechanism.The optimal length ratios of links were decided via dexterity and reliability.The parameterization simulation model was built in ADAMS.Simulation result according with the analysis by theory indicates that the optimization and con figuration are correct and suitable.This method provides a basis for the development of actual pro to and the control of bionic cockroach robot.It also can be referable for the design of other hexapod robots.

bionic cockroach robot;dexterity;optimization;Jacobian matrix

TP 242

A

1001-5965(2010)05-0513-05

2009-06-15

国家 863计划资助项目(2008AA 04Z210);国家自然科学基金资助项目(60775059);北京市自然科学基金资助项目(3093021)

张建斌(1960-),男,江西萍乡人,教授,jbzhang@buaa.edu.cn.