三角网格曲面模型快速分层算法

孙殿柱 朱昌志 李延瑞

(山东理工大学 机械工程学院,淄博 255091)

三角网格曲面模型快速分层算法

孙殿柱 朱昌志 李延瑞

(山东理工大学 机械工程学院,淄博 255091)

提出一种三角网格曲面模型快速分层算法,该算法基于 R*-tree建立三角网格动态空间索引结构,依据索引结构数据结点的分布状况计算各层截平面的位置;采用深度优先遍历方法获取与截平面相交的三角面片集合,并计算该集合中各面片与截平面的交线,将交线首尾相连,生成截面轮廓线,实现三角网格曲面模型的快速分层;实例证明该算法可对各种复杂三角网格曲面模型进行分层,算法准确、稳定,运行效率高.

三角网格曲面模型;R*-tree;深度优先遍历;截面轮廓线;快速分层

快速成型制造中,通常将 CAD模型离散为三角面片,生成三角网格曲面模型,随后进行分层处理生成截面轮廓线,采用光敏树脂等材料堆积出与截面轮廓线形状一致的薄层,逐层累加,得到零件的实体模型.高效准确地对三角网格曲面模型进行分层处理是快速成型制造的首要条件[1].

目前,三角网格曲面模型的分层方法主要有2类:第 1类基于三角网格拓扑关系进行分层[2-3];第 2类基于三角面片几何特征进行分层[1,4-5].

第 1类方法建立三角面片邻接关系表,令第1个与截平面相交的三角面片为初始面片,计算其与截平面的交线段,依据邻接关系表查询初始面片的邻接三角面片,并计算该面片与截平面的交线,依次追踪,直至得到当前层封闭的截面轮廓线;重复上述过程获取所有层的截面轮廓线,实现三角网格曲面模型的分层处理.该方法需建立三角面片邻接关系表,系统资源消耗高,算法运行效率低.

第 2类方法分别依据三角面片 z坐标的最小值和最大值对所有三角面片排序,得到最小值序列和最大值序列;在分层处理时,分别遍历两序列,排除最小 z值大于截平面高度和最大 z值小于截平面高度的面片,得到与截平面相交的三角面片,并计算其与截平面的交线,将交线首尾相连,得到截面轮廓线.该方法需对三角面片进行 2次排序,且查询相交三角面片时分别遍历最小值序列与最大值序列,算法运行效率低.

针对上述问题,提出一种三角网格曲面模型的快速分层算法,该算法基于 R*-tree[6-8]建立三角网格动态空间索引结构,以该结构组织三角面片间的拓扑关系,基于该结构计算各层截平面的位置并获取与截平面相交的三角面片集合,计算集合中各面片与截平面的交线,并将交线首尾相连,生成截面轮廓线;最后通过 2组实验方案验证了该算法的可行性.

1 动态空间索引结构的建立

通过改进 R*-tree建立三角网格动态空间索引结构,实现三角网格的动态存取及相交三角面片的快速查询.

1.1 索引结点规范化表示

R*-tree结点插入算法以 MBR(Minimum Bounding Rectangle)体积增量[9]作为结点聚类分簇的判定条件,该算法应用于三角面片集合的空间聚类分簇时,若局部三角面片平行于坐标平面分布,结点的 MBR将由三维退化为二维,体积增量为零,导致 R*-tree结点插入失效,破坏了R*-tree结点的聚合性.为解决该问题,如图 1所示,将三角面片及索引结构的结点MBR统一表示为四维点对象(x,y,z,r),其中 x,y,z为结点 MBR中心坐标,r为结点 MBR外接球半径.

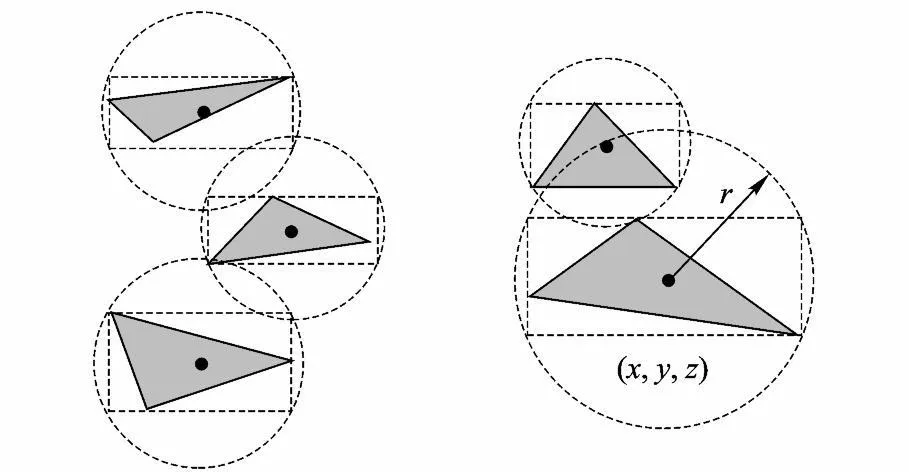
图1 索引结点规范化表示

1.2 三角面片集合的 k-m eans聚类分簇

采用 k-means算法[10]实现三角面片集合的空间聚类分簇.在选取初始分簇中心时,为减少 kmeans迭代次数,将结点中心相距最远的一对结点的 MBR中心作为初始分簇中心.

确定初始分簇中心后,将数据对象添加到中心距其最近的分簇中.为使结点 MBR均匀,避免出现 MBR奇异的结点,根据 R*-tree定义,若分裂所得结点的子结点数 k小于 R*-tree最小子结点数 m,则将另一簇中距离当前簇较近的(m-k)个结点插入到当前簇中,并调整分裂结果.

采用 k-means算法对 R*-tree索引结点进行聚类分簇,需要迭代定位最终的分簇中心.对于同簇结点中的 N个索引结点,其四维标准化坐标为分簇中心坐标)可由下式计算:

各索引结点至聚类分簇中心的距离,可由公式(1)计算:

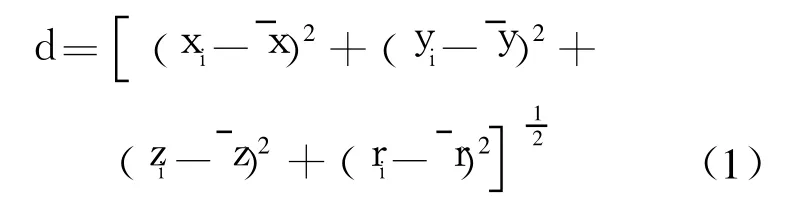
该索引结构由 4种结点组成,最上层为根结点,最底层为数据结点,次底层为叶结点,其余为内部结点,每个数据结点存储一个三角面片.基于四维点表示的三角网格动态空间索引结构如图 2所示.

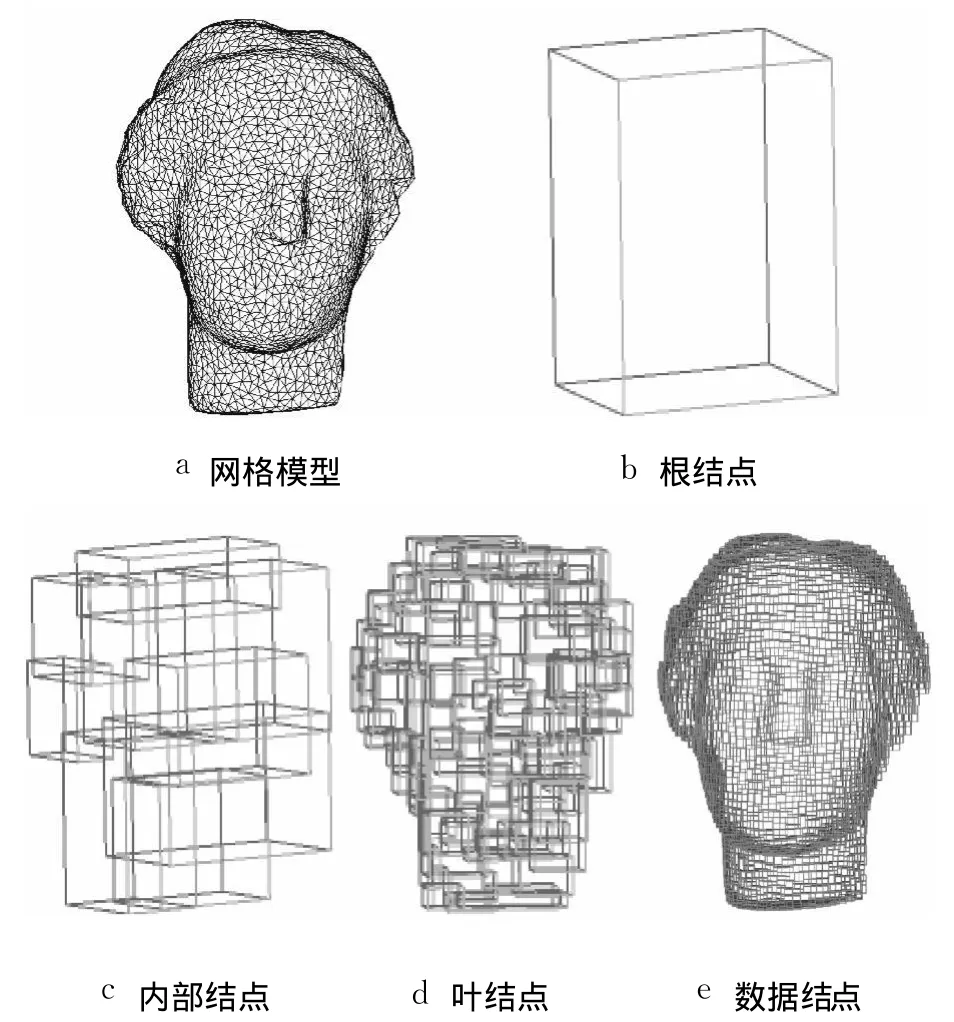
图2 维纳斯头像网格模型的空间索引结构

2 三角网格曲面模型的快速分层

2.1 索引结点与截平面的位置关系

令索引结点的顶点为 vi(1≤i≤8),q为截平面上任意点,n为截平面的法矢,采用公式(2)判断索引结点与截平面的位置关系.

若 εi＜0,表示索引结点位于截平面负侧;若 εi＞0,表示索引结点位于截平面正侧.如图 3a所示,若索引结点 8个顶点的 εi值均为正(或负),则表示该结点与截平面相离;如图 3b所示,若 εi的值不同时为正(或负),表示该结点与截平面相交.

图3 索引结点与截平面的位置关系

2.2 截平面位置的计算

设截平面平行于 xOy平面分布,法矢 n指向z轴正方向,三角网格在 z轴上的极值为 zmin与zmax,采用公式(3)计算初始截平面位置:

其余各层截平面的位置可由公式(4)计算:

令与第 i层截平面相交的数据结点集合为 L,则 εj为 L中各数据结点的顶点距截平面的距离,由公式(2)计算;n为 L中位于截平面正侧(即εj＞0)的数据结点顶点数;μ为控制层数的参数,与层数成反比,通常取 1.0.

2.3 相交三角面片的获取

基于以上判断法则,深度优先遍历三角网格动态空间索引结构,获取与截平面相交的三角面片,具体步骤如下:

1)输入 R*-tree根结点;

2)若当前结点为数据结点,判断该结点与截平面的位置关系,若相交,则将该结点包含的三角面片添加到相交三角面片序列 L中;

3)若结点为内部结点,则循环取得当前结点的子结点,执行步骤 2).

2.4 交线段的计算及排序

如图 4所示,三角面片与截平面相交存在以下 3种情况,交线段的计算方法如下:

1)若有 2点落在截平面上,则以该 2点组成的线段为交线段;

2)若无点落在截平面上,则依据三角面片各顶点计算交线段;

3)若只有一点落在截平面上,则不计算其与截平面的交线段.

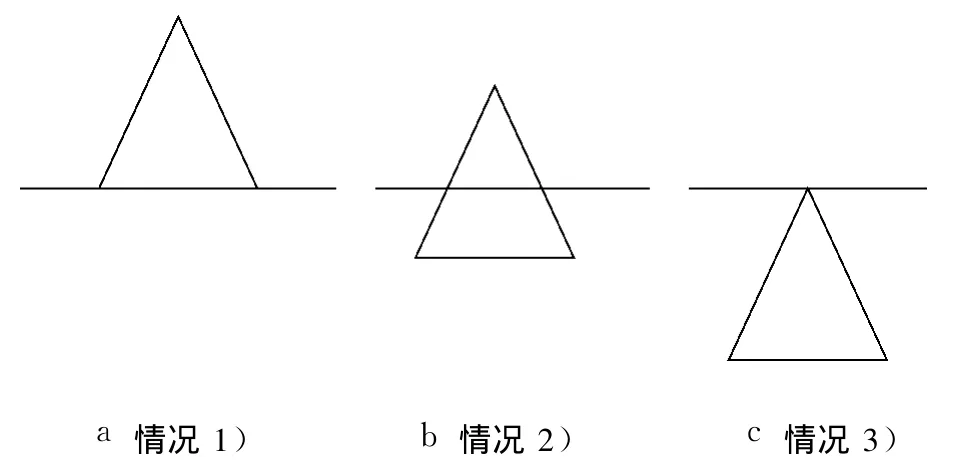
图4 三角面片与截平面的位置关系

采用文献[1]算法将交线段首尾相连,得到有序的截面轮廓线,实现三角网格曲面模型的分层处理.

3 应用实例

制定 2组实验方案对本文算法进行验证.方案 1采用本文算法及相关算法对同一三角网格曲面模型进行分层处理,分析不同算法的分层效果;方案 2采用本文算法及相关算法对不同三角网格曲面模型进行分层,分析不同算法的运行效率及适应性.

方案 1中,采用本文算法及文献[5]算法对图 5a所示三角网格模型进行分层处理,层数均为50,分层效果如图 5b和图 5c所示.可以看出,本文算法分层处理后的模型在型面特征复杂区域截面数据分布较为密集,在平坦区域截面数据分布较为稀疏,达到了准确表达模型外形信息的目的.

图5 b lade模型及分层效果

方案 2中,采用本文算法及文献[5]算法对图 6所示的 4种三角网格模型进行分层,各模型的三角面片数分别为 12 520,40 168,1 087 716,1765388,将各模型分为 50层,各算法运行时间如表 1所示.可见,本文算法有效提高了三角网格曲面模型的分层效率,平均提高 30%～50%.

图6 三角网格模型

表 1 不同算法的运行时间 s

4 结 论

本文算法与相关算法相比具有以下优点:

1)基于 R*-tree建立三角网格曲面模型动态空间索引结构,可对各种复杂型面三角网格曲面模型进行分层,算法适应性强;

2)依据索引结构各层数据结点的分布情况计算相邻层截平面的位置,有效提高了分层数据的准确性;

3)基于三角网格动态空间索引结构,快速准确地获取与截平面相交的三角面片,提高了三角网格曲面模型的分层效率.

References)

[1]胡德州,李占利,李涤尘,等.基于 STL模型几何特征分类的快速分层处理算法研究[J].西安交通大学学报,2000,34(1):37-40 Hu Dezhou,Li Zhanli,Li Dichen,et al.Algorithm for rapid slicing based on geometric feature classification of STLmodel[J].Journal of Xi'an Jiaotong University,2000,34(1):37-40(in Chinese)

[2]Pan Haipeng,Zhou Tianrui.Generation and optimization of slice profile data in rapid prototyping and manufacturing[J].Journal of Materials Processing Technology,2007,187/188:623-626

[3]赵吉宾,刘伟军.快速成形技术中基于 STL模型的分层算法研究[J].应用基础与工程科学学报,2008,12(6):224-233 Zhao Jibin,Liu Weijun.Research on slicing algorithm based on STLmodal for rapid prototyping technology[J].Journal of Basic Science and Engineering,2008,12(6):224-233(in Chinese)

[4]赵保军,汪苏,陈五一.STL数据模型的快速切片算法[J].北京航空航天大学学报,2004,30(4):329-333 Zhao Baojun,Wang Su,Chen Wuyi.Algorithm for rapid slicing STLmodel[J].Journal of Beijing University of Aeronautics and Astronautics,2004,30(4):329-333(in Chinese)

[5]李占利,梁栋,李涤尘,等.基于信息继承的快速分层处理算法研究[J].西安交通大学学报,2002,36(1):43-46 Li Zhanli,Liang Dong,Li Dichen,et al.Algorithm for rapid slicing based on the information inheriting[J].Journal of Xi'an Jiaotong University,2002,36(1):43-46(in Chinese)

[6]孙殿柱,朱昌志,李延瑞.散乱点云边界特征快速提取算法[J].山东大学学报:工程科学版,2009,39(1):84-86 Sun Dianzhu,Zhu Changzhi,Li Yanrui.An improved extraction of boundary characteristic from scattered data[J].Journal of Shandong University:Engineering Science,2009,39(1):84-86(in Chinese)

[7]孙殿柱,范志先,李延瑞,等.散乱数据点云型面特征分析算法的研究与应用[J].机械工程学报,2007,43(6):133-136 Sun Dianzhu,Fan Zhixian,Li Yanrui,et al.Research and application of surface feature analysis for scatter data points[J].Chinese Journal of Mechanical Engineering,2007,43(6):133-136(in Chinese)

[8]孙殿柱,李心成,范志先,等.采用 R*-tree的三角网格曲面非均匀精简算法[J].西安交通大学学报,2008,42(9):1179-1183 Sun Dianzhu,Li X incheng,Fan Zhixian,et al.Simplified algorithm for triangular mesh surface based on R*-tree[J].Journal of Xi'an Jiaotong University,2008,42(9):1179-1183(in Chinese)

[9]张明波,陆锋,申排伟,等.R树家族的演变和发展[J].计算机学报,2005,28(3):289-300 Zhang Mingbo,Lu Feng,Shen Paiwei,et al.The evolvement and progress of r-tree family[J].Chinese Journal of Computers,2005,28(3):289-300(in Chinese)

[10]Brakatsoulas S,Pfoser D,Theodoridis Y.Revisiting R-tree construction principles[C]//Manolopoulos Y,Ndvrat P.6th East European Conference on Advances in Databases and Information Systems.London:Springer-Verlag,2002:149-162

(编 辑:文丽芳)

Fast slicing algorithm for triangular mesh model

Sun Dianzhu Zhu Changzhi Li Yanrui

(School of Mechanical Engineering,Shandong University of Technology,Zibo 255091,China)

A fast slicing algorithm for triangular mesh model was proposed.The node splitting algorithm and the clustering algorithm of R*-tree were improved and the spacial index structure of triangular mesh model was established based on the improved R*-tree.The position of slice planes was computed according to data nodes'distributing of the spacial index structure,thus the distribution of slice planes was intensive in the cragged region of triangular mesh,and the distribution of slice planes was sparse in the smooth region of triangular mesh.The intersection triangular facets with slice plane were obtained with depth-first traversal algorithm of R*-tree.The intersection line segments between slice plane and interection triangular facets were computed and they were sorted end to end,then the orderly section contour lines were obtained.It was proved that this algorithm can obtain section contour line accurately,effectively and has strong adaptability of triangular mesh model.

triangular mesh;R*-tree;depth-first traversal;section contour line;slicing algorithm

TP 391.72

A

1001-5965(2010)03-0279-04

2009-02-27

国家 863计划资助项目(2006AA 04Z105)

孙殿柱(1956-),男,山东烟台人,教授,zhuchzhi@126.com.