考虑土渐近状态特性的应力应变关系

罗 汀 田新国

(北京航空航天大学 交通科学与工程学院,北京 100191)

考虑土渐近状态特性的应力应变关系

罗 汀 田新国

(北京航空航天大学 交通科学与工程学院,北京 100191)

在经典弹塑性理论框架下,根据 SMP(Spatially Mobilized Plane)破坏准则并结合变换应力方法,通过引入准弹性体积模量的概念,建立了用增量法表示的考虑土渐近状态特性的三维应力应变关系式.针对三轴压缩应力条件,给出了相应的简化应力应变增量矩阵,以三轴压缩试验中的常规三轴压缩、不排水剪切和控制应变增量比的 3种应力路径为例,推导出了便于应用的应力应变增量关系式.最后,利用文中的公式进行了预测分析和试验对比,结果表明:新推导的公式能方便地预测考虑渐近状态特性下土的应力应变关系,并能合理描述试验结果.

土;渐近状态;弹塑性;应力应变关系

地基中饱和土通常是在某种约束下受力变形的,这种变形约束会影响到土的应力应变关系,即对于同一种土,不同的变形约束条件会对应着不同的应力应变规律.而且在变形约束下的剪切受力极限应力比有时会比峰值破坏应力比低很多.作者等在土的统一硬化模型[1]的基础上,采用耦合硬化和非耦合硬化相结合的思路提出了一个能反映饱和砂土渐近状态特性的本构模型[2],该模型能够合理预测各种复杂应力路径下的应力应变规律,也包括合理预测各种路径下的极限应力比.

地基中的应力状态一般是三维的,如果不对已经提出的反映渐近状态特性的本构模型合理三维化,在三轴压缩以外应力状态的土的应力应变特性还是得不到合理描述.本文在经典弹塑性理论的框架下,建立了用增量法表示的考虑渐近状态特性的土应力应变关系式,合理考虑了非耦合部分塑性应变增量的计算.对于三维应力状态,给出了结合变换应力方法的三维应力应变增量矩阵,也即弹塑性本构张量.针对土工试验中常见的各种应力路径,推导出便于应用的应力应变关系式.此外还应用文中的应力应变公式进行了预测分析.

1 渐进状态模型

考虑到不同约束条件下砂土具有不同的峰值强度,为了能够合理地表示不同约束条件的影响,把硬化参量 H分解为耦合硬化参量 Hc和非耦合硬化参量 Hunc两部分,硬化参量的耦合部分表示塑性体积应变与平均正应力 p和广义剪应力 q均相关,硬化参量的非耦合部分表示塑性体积应变只由平均正应力 p引起,与广义剪应力 q无关,其中定义的耦合参量 μ可以由峰值应力比 Mf和特征状态应力比 M求出.

渐近状态模型中体积应变增量和广义剪切应变增量定义为

式中,＜μ＞表示弹塑性区 ＜μ＞=μ,弹性区＜μ＞=0;cp=(λ-κ)/(1+e0);e0为初始孔隙比;λ和 κ分别是根据等向固结试验得出的压缩和回弹参数.设

式(1)还可以表示为

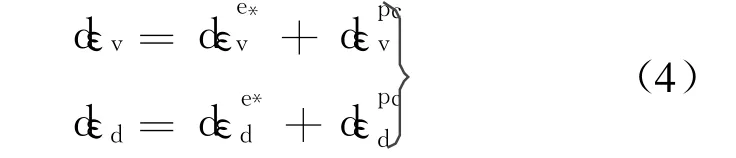
式(4)中的弹性部分因为加入了非耦合部分的影响,所以称为准弹性部分.有了式(4),就可以用类似于普通弹塑性理论建立应力应变关系那样建立增量公式.

渐进状态模型中的耦合塑性应变部分仍由常规的弹塑性理论方法导出.

2 三维化方法

在通常情况下,弹塑性模型三维化是通过假设其屈服面在 π平面上为圆形来实现的,模型的剪切屈服和剪切破坏均采用扩展 Mises准则.而土材料三轴压缩和三轴拉伸的强度明显不同,SMP(Spatially Mobilized Plane)破坏准则[3]能合理表示这种情况.

为了能够合理地描述不同情况下的应力应变关系,可以采用变换应力的方法把 SMP外凸三角形变换为圆形,在变换应力空间建立本构模型就可以反映三维应力应变关系特点.变换应力计算公式[4]为

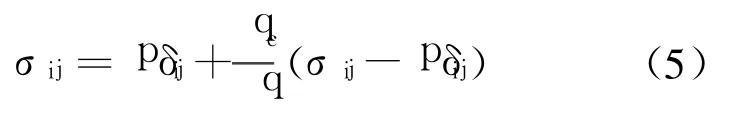
式中 ,当 i=j时 δij=1,当 i≠j时 δij=0;qc是 SMP线在三轴压缩条件下的对应值为

式中,I1,I2,I3为应力不变量.在变换应力空间平均正应力和广义剪应力分别为

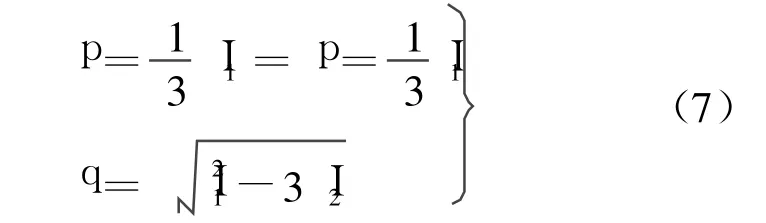
在变换应力空间屈服函数为

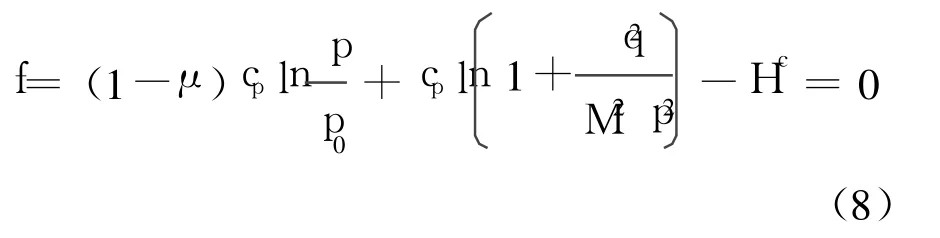
若取η=q/p,硬化参数 Hc为

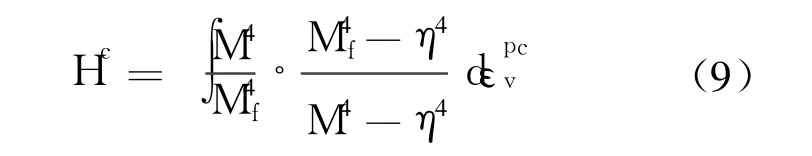
塑性势函数为

式中,px为塑性势面与p轴的交点.

3 基于弹塑性理论的增量公式

由一般的弹塑性理论可知,应力增量与应变增量弹塑性本构张量[5]可写为

考虑非耦合塑性应变后:

其中准弹性本构张量可表示为

式中,L*和 G称为拉梅常数:

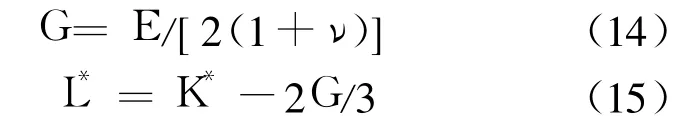
把等向固结试验结果在 e-ln p坐标系中进行整理,其关系为线性关系的土材料,弹性模量可写为E=3(1-2ν)(1+e0)p/κ,ν是泊松比,K*是考虑非耦合塑性应变后的准弹性体积模量.

下面推求 K*,若应力和应变分别用 p,q,εv,εd表示,根据弹性理论,弹性应变增量与应力增量的关系为

式中,体积模量 K=E/[3(1-2ν)];De是弹性刚度矩阵,把式(2),式(16)代入式(3)可得

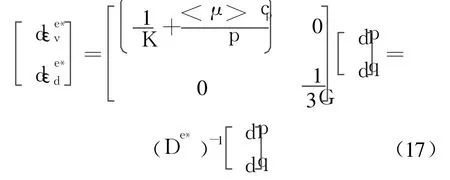
由式(17)可得

所以

根据弹塑性本构理论,经推导得

由屈服函数式(8)求得

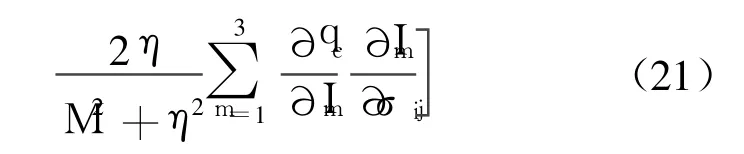
式中,Im=I1,I2,I3.

由塑性势函数式(10)求得

把式(21),式(22)代入到式(20),即可得到考虑了土的三维化的渐进状态模型应力应变增量张量.对于三轴压缩情况,p=p,q=q,此时式(20)中的弹塑性本构张量可以较为简捷地表示出来.

4 三轴压缩情况

4.1 基本公式

对于实验室常用的三轴压缩情况,式(20)可简化为二维形式,用矩阵表示为

经推导,可得弹塑性刚度矩阵 Dep中的 4个系数分别为

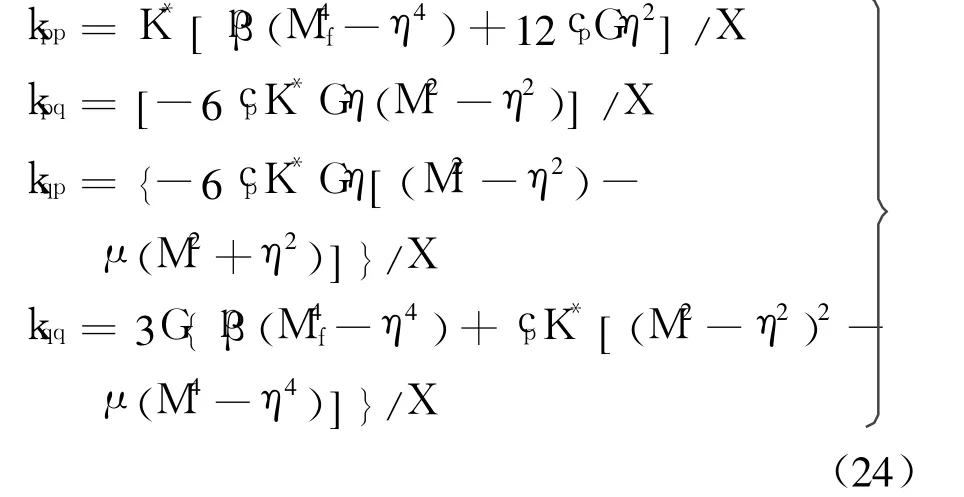
由屈服函数式(8)可知,当耦合参数μ=0,并且 Mf=M时,就是修正 Cam-clay模型,因此在弹塑性刚度矩阵系数式(24)中,取 μ=0,和 Mf=M(β=1),就可以得到修正 Cam-clay模型的弹塑性刚度矩阵 Dep.

4.2 特殊应力路径下的应力应变增量公式

在三轴压缩试验中常见的应力路径有固结不排水应力路径,σ3=c路径等,可以根据式(23)、式(24)预测不同应力路径下考虑渐进状态特性的应力应变关系.试验中一般体积应变增量和剪应变增量不会直接给出,而垂直应变增量 dε1在试验中是可以控制的.预测时模拟试验过程,给出垂直方向的应变增量 dε1,求出水平方向的应变增量、应力增量 dε3,dσ1,dσ3分别与 dε1的关系,其它的应力应变关系就很容易得到.

在三轴压缩条件下

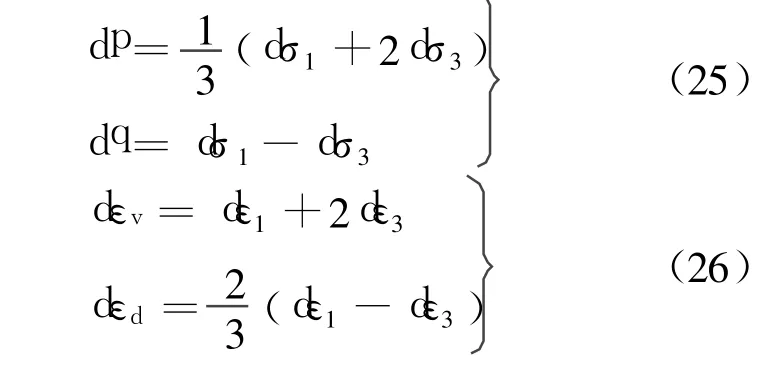
根据不同的应力路径条件和式(23)～式(26)可以分别求出不同应力路径时径向应变增量和主应力增量.

1)固结不排水剪切路径.

固结不排水试验是在某设定的围压下固结,然后在不排水条件下剪切至破坏.把剪切过程中的条件 dεv=0和式(25)、式 (26)代入式(23)得

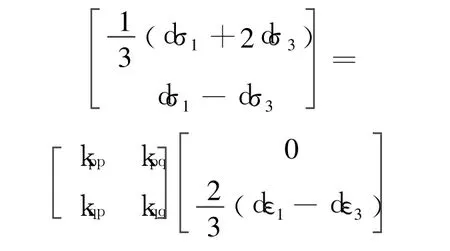
整理上式得

2)路径 σ3=c.

这是实验室常用的围压为常数的试验,把试验条件 dσ3=0和式 (25)、式 (26)代入式 (23)整理得

对于其他的应力路径也可以参照上述方法得出相应的计算公式.

5 模型预测

取土性参数为[6]ν=0.3,M=1.00,Mf=1.57,λ=0.0048,κ=0.002 8,e0=0.614,根据渐进状态模型可求得 M0=1.33,μ=0.54.图 1是预测与实际的比较,图 1a是应力路径,图 1b是应力应变关系.①号线是不排水剪切试验及预测结果;②号线是控制应变比 n=-0.43的试验及预测结果.由图可知,不同的变形约束条件对应着不同的应力应变规律,预测结果与试验结果符合较好.

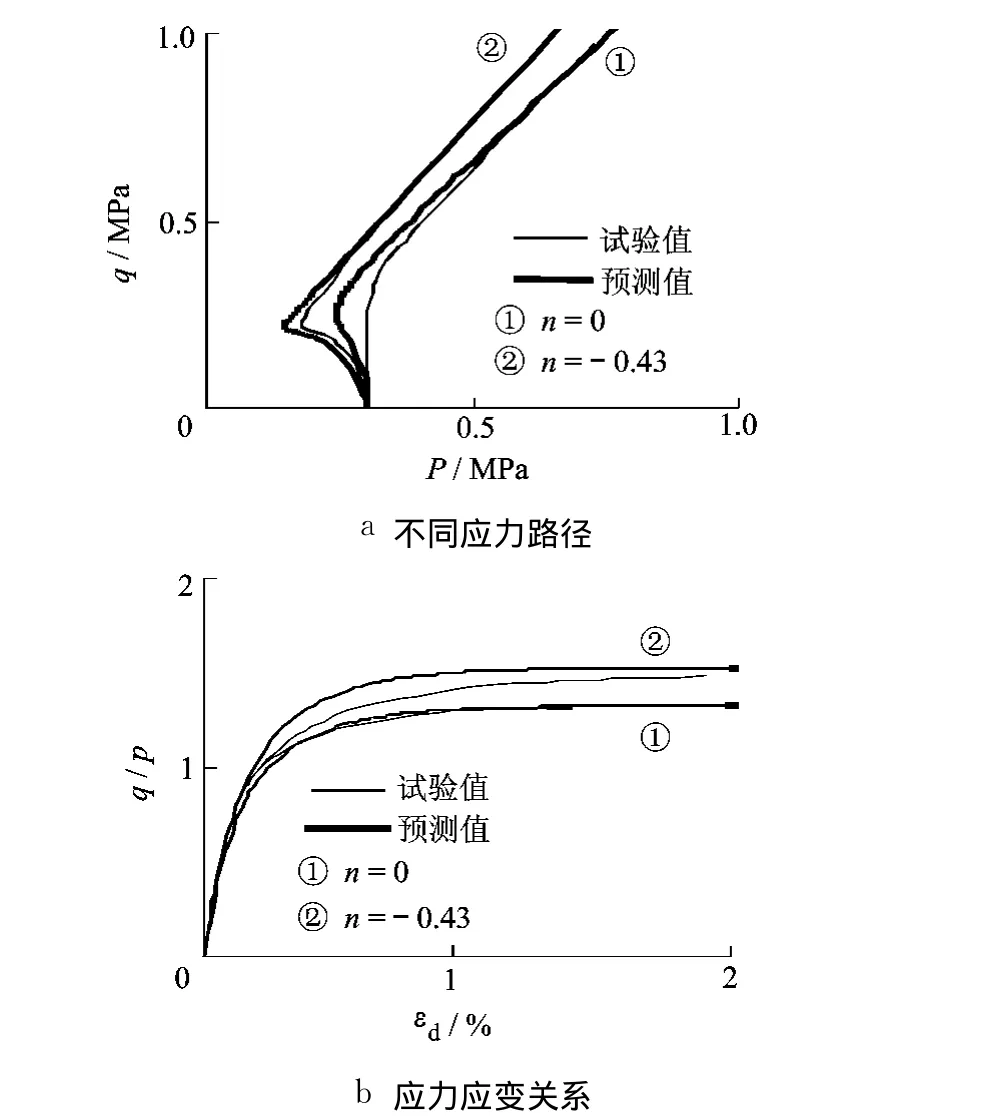
图1 渐进状态模型预测与实测比较

6 结 论

1)考虑渐进状态特性的本构模型,实质就是考虑复杂应力路径影响的本构模型,本文建立了考虑渐近状态特性土的三维应力应变本构张量.

2)对于常见的三轴试验应力路径,推导出了便于应用的应力应变增量关系,修正 Cam-clay模型是其特例.通过实例表明,本文的方法能方便地预测考虑渐近状态特性下土的应力应变关系,并能合理描述试验结果.

References)

[1]Yao Y P,Sun D A,Matsuoka H.A unified constitutive model for both c lay and sand with hardening parameter independent on stress path[J].Computers and Geotechnics,2008,35:210-222

[2]Luo Ting,Yao Yangping,Chu Jian.Asymptotic state behaviour and its modeling for saturated sand[J].Science in China(Ser E),2009,52(8):2350-2358

[3]Matsuoka H,Nakai T.Stress-deformation and strength characteristics of soil under three different principal stresses[J].JSCE Proceedings of the Japan Society of Civil Engineers,1974,232:59-70

[4]Matsuoka H,Yao YP,Sun D A.The cam-clay models revised by the SM Pcriterion[J].Soils and Foundations,1999,39(1):81-95

[5]松岡元.地盤工学の新しいアプローチ[M].日本:京都大学学術出版会,2003 Matsuoka H.A newmethod for geotechnique[M].Japan:Kyoto University Press,2003(in Japanese)

[6]Chu J,Lo SCR.Asymptotic behaviour of a granular soil in strain path testing[J].Geotechnique,1994,44(1):65-82

(编 辑 :张 嵘)

Stress-strain incremental law in asymptotic state for soils

Luo Ting Tian Xinguo

(School of Transportation Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Based on the classicalelasto-plastic theory,the transformed stress space deduced from the spatially mobilized plane(SMP)criterion and a new concept of similar elastic volume modulus,the stress-strain incremental equations of soils for the asymptotic state constitutive model were established.A simple stress strain incremental matrix under triaxial compression condition was formulated,in which the modified Cam-clay model was a special case.The stress-strain incremental equations were then proposed to simulate the stress strain relationships in some triaxial stress path tests as the triaxial compression,the consolidated undrained and the strain incremental ratio controlled.The proposed equations were used to simulate and compare the triaxial test results.They show that the equations proposed can be used easily and the asymptote state model can describe the stress-strain and strength behaviors of soils reasonably.

soils;asymptotic state;elastop lastic;stress-strain relationship

TU 431

A

1001-5965(2010)03-0315-04

2009-01-01

国家自然科学基金资助项目(50879001,10872016,90815024)

罗 汀(19 57-),福建长汀人,女,副教授,tluo@buaa.edu.cn.