基于确定性和随机性原理的复合材料二维孔隙模型比较

张 翔， 林 莉， 陈 军， 郭广平， 李喜孟

(1.大连理工大学无损检测研究所，辽宁大连116024;2.北京航空材料研究院，北京100095)

孔隙是复合材料最常见且对使用性能有重要影响的缺陷［1～3］。由于孔隙会导致复合材料的层间剪切强度、弯曲强度、纵/横向拉伸强度等性能下降，因此对孔隙率的鉴定是判断复合材料质量的重要手段。依据构件重要程度不同，复合材料孔隙率通常控制在1%～2.5%，准确可靠的孔隙率(1%～5%)无损检测技术成为航空航天领域的迫切工程需求［2］。

目前受到广泛认可的孔隙率检测方法是超声衰减法，即通过测量超声衰减系数的大小来确定层压板内部的孔隙含量。此研究的核心内容是孔隙的超声散射衰减数学模型和物理机制，其重要前提是建立合理的孔隙形貌特征描述模型。二十世纪七十年代，沿用传统的金属材料超声检测的思想和模式，Martin借鉴Hashin提出的含孔隙均匀、各向同性固体介质的弹性理论［4］，研究了含有离散分布球形孔隙复合材料中的超声纵波和横波散射情况，率先建立了孔隙率超声散射衰减模型［5，6］。此后，Hale和Ashton假定孔隙为球状或圆盘状且尺寸符合不同函数的分布［7］，对 Martin提出的模型作了改进。Jeong，Hsu等人在利用超声频域法检测时，又将孔隙假设为具有椭圆截面的长圆柱形状进行了实验和理论研究［8］。浙江大学周晓军等人对孔隙形状与分布做了更为细致的假设和描述，对模型进行了完善［9］。尽管上述各模型中对孔隙形状、尺寸的假设有所不同，但它们的理论依据都是Martin所采用的含孔隙各向同性均匀介质弹性理论，都假设孔隙具有某种确定的、规则的几何形状，且超声波波长远大于孔隙尺寸，即超声波散射与孔隙形状无关。然而，上述理论模型与实验结果之间仅在部分孔隙率范围和某些特定频率下取得定量对应关系，至今尚未建立具有普遍意义的复合材料孔隙超声衰减检测模型以及完善的孔隙超声衰减机理。

最近的研究发现，尽管孔隙率在孔隙与各种场(如超声场)的相互作用以及与复合材料性能相关的研究中起到重要作用，然而，孔隙形状、尺寸、取向及数量等形貌特征因素也不能忽略［10］。在研究孔隙对复合材料性能的影响时，仅仅考虑孔隙率的变化并不全面，还必须考虑孔隙微观形貌的影响。然而，由于制备工艺的特点，导致复合材料构件的组织结构及性能具有明显的随机性和不确定性。真实孔隙形貌十分复杂，它们不但尺寸变化范围大，从几微米到几十、甚至几百微米，而且无序分布，同时孔隙形状还很不规则，边界粗糙，从数学和物理角度都很难处理。

针对上述问题，本课题组率先将随机介质理论引入到复合材料孔隙的描述中，依据统计学原理，基于显微观察法获得不同孔隙率试样中的大量孔隙形貌照片及对孔隙形状、尺寸及分布等进行统计分析和数据处理的结果，建立了二维随机孔隙模型［11，12］。本研究通过比较以Martin为代表建立的确定性孔隙模型与随机孔隙模型的建模思想和研究结果，试图找到更为合理的孔隙形貌特征描述原理和方法，建立有效的复合材料孔隙率超声衰减法检测模型。

1 基本原理

超声波的散射强烈依赖于介质的弹性特性，为了准确表征复合材料孔隙率及其变化情况，必须研究孔隙引起的弹性参数变化对超声波传播的影响，其外在表现之一则是超声衰减系数的变化。

1.1 确定性模型

Martin借鉴Hashin提出的含孔隙均匀、各向同性固体介质的弹性理论，研究了含有离散分布球形孔隙复合材料中的超声纵波和横波散射情况，基于基体为含孔隙的各向同性介质，所有孔隙为半径相等、均匀分布的球形，超声波波长远大于孔隙尺寸等假设条件，率先建立了孔隙率超声检测模型。此后，Hale和Ashton对Martin提出的模型作了改进，给出了超声衰减系数的表达式［7］:

式中，αV是超声衰减系数，P是材料的体积孔隙百分含量，ρt是无孔隙材料理论密度，f是超声频率，E是弹性模量，a是孔隙半径，g是材料常数，g值由下式决定:

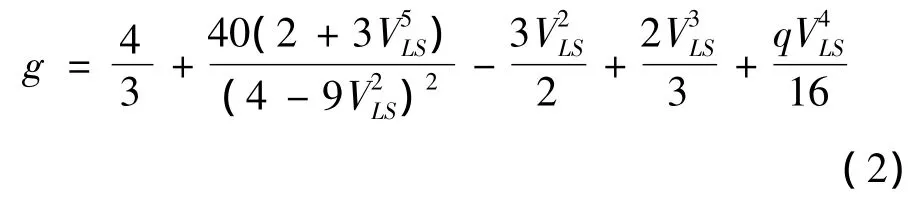
1.2 随机孔隙模型

随机介质模型是针对非均匀介质提出的统计学描述方法，它由大、小两种尺度的非均匀性所组成。大尺度的非均匀性描述介质的平均特性，而小尺度的非均匀性是加在上述平均值上的随机扰动。以二维随机介质为例，在空间点(x，z)处的弹性参量M (x，z)(密度、拉梅常数等)可分解为［13］:

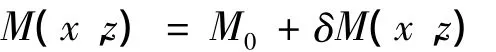
式中:M0为大尺度非均匀性参数，假设为常数或随二维空间坐标(x，z)缓慢变化;x和z分别为二维直角坐标系的水平与垂直方向坐标;δM为加在前者之上的小尺度非均匀扰动量，并假设其为具有零均值、一定方差及某一自相关函数的空间平稳随机过程，于是介质的弹性参数在小尺度上的空间扰动就可以用空间自相关函数、相关长度、均值及标准差等几个统计量来描述。对于含孔隙复合材料而言，反映背景介质弹性特性的超声纵波、横波速率及密度均可以通过实验直接测得;用于描述孔隙带来的弹性参数随机扰动的统计参量，则可根据由显微照相法对孔隙形态特征进行观测、统计得到的数据，借助数学手段获得。

依据上述原理和方法，可以建立适合于描述复合材料孔隙形貌的随机孔隙模型［14］。为了计算不同孔隙率条件下的超声衰减系数，需要对弹性波方程进行求解。弹性固体中声场问题只有对简单几何形状才可能有解析解，随机孔隙模型较为复杂，因此采用时域有限差分法求解固体中的波动方程，进而计算超声衰减系数。具体计算方法请参考其他文献，此处不予赘述。

2 实验

实验样品为16层预浸料热压成型碳纤维单向增强环氧树脂基复合板，厚度2mm，纤维体积含量(69±3)%。该复合板面积大于200 mm×250mm。通过控制热压成型过程中的压力，得到孔隙率变化范围为0.03%～4.62%的试件。

超声衰减系数的测量选用底板反射回波法［15］，超声检测仪器为USIP40超声探伤仪，所用探头为MATEC-ISO504GP平探头，晶片直径12.5mm，频率5MHz。采用MeF4A金相显微镜进行孔隙率统计及孔隙形态的显微分析。

3 模拟结果

3.1 孔隙几何相似性

比较由Martin提出的确定性模型和随机孔隙模型所模拟的孔隙形貌的几何相似性。图1为孔隙率P=1.5%和P=4.62%时，由两种模型模拟的含孔隙复合材料物理模拟结果与金相照片的对比情况。观察发现，Martin提出的确定性模型假设孔隙全部为大小相等、离散均匀分布的球形，与实际孔隙的几何相似性差别较大。而由随机孔隙模型模拟的孔隙，在形状、尺寸、取向及分布等特征方面均表现出明显的随机性，与实际孔隙之间的几何相似性较好。

图1 确定性模型和随机孔隙模型得到的孔隙形貌与孔隙显微照片比较Fig.1 Comparison of void morphology from deterministic model and random void model (a)deterministic model(P=1.5%); (b)void morphology from microscope(P=1.5%);(c)random void model(P=1.5%);(d)deterministic model(P= 4.62%);(e)void morphology from microscope(P=4.62%);(f)random void model(P=4.62%)

3.2 孔隙引起的超声衰减

3.2.1 孔隙率与衰减系数对应关系

以孔隙率1.5%为例，比较利用Martin提出的确定性模型和随机孔隙模型计算超声衰减系数的差异。由公式(1)和(2)，可以计算出Martin模型对应的超声衰减系数α=0.029dB/mm。随机孔隙模型由于考虑到孔隙形貌特征的随机性，因此，即使在同一孔隙率下，也可以得到若干不同的孔隙形貌分布图，此处随机选取其中的12幅含孔隙复合材料物理模拟结果，如图2所示。进一步利用时域有限差分正演方法，计算得到相应的超声衰减系数，如图3所示。观察发现，孔隙率不变的情况下，孔隙形貌特征的随机性会引起超声衰减系数的波动，P=1.5%时，α的波动范围为3.62～4.17dB/mm，相对波动约为13%。即，对于给定的复合材料，利用确定性的Martin模型，每一个孔隙率对应一个确定的超声衰减系数;而依据随机孔隙模型，一个孔隙率对应着一个衰减系数的变化范围。

图2 利用随机孔隙模型得到的含孔隙复合材料物理模拟结果Fig.2 Modeling results of composites containing voids from random void model(void content P=1.5%)

3.2.2 衰减系数理论预测值与实验结果对比

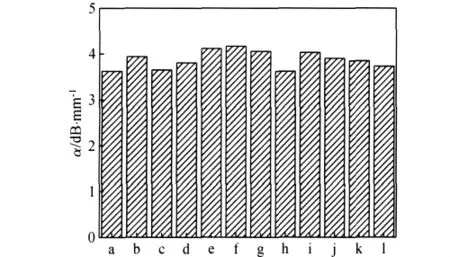
图3 对应图2模拟结果(a～l)的超声衰减系数变化情况Fig.3 Ultrasonic attenuation coefficient(f=5MHz)of simulation results for a～l in Fig.2

图4为5MHz下，复合材料孔隙率与超声衰减系数理论预测和实验测试对比结果。观察发现，随着孔隙率增加，衰减系数实验值不断增加。且对于孔隙率小于0.5%的试样，衰减系数增加的速率要小于孔隙率大于0.5%的试样。如将本实验研究的复合材料孔隙全部看做是大小相等、均匀分布的球体，则折算过来的球形孔隙平均半径为21.2μm，按此数据，依据Martin模型可以算出相应的衰减系数理论值。可以看出，利用此模型得到的衰减系数随着孔隙率的增加变化不大，尤其在孔隙率小于2%阶段，衰减系数几乎保持不变，整体上的理论衰减系数远远小于实验测试结果。为了使Martin模型的预测结果与实验结果接近，只能进一步增加孔隙的平均半径。研究发现，当球形孔隙半径增加到60μm时，对应的超声衰减系数计算值与实验测试结果相当，表明Martin的确定性模型大大低估了实际孔隙造成的超声衰减。对于利用随机孔隙模型得到的理论预测值，可以看出，随着孔隙率的增加，相应的衰减系数计算结果不断增加，二者之间的符合程度远远优于Martin的确定性模型。另外值得关注的是，对于孔隙率3.8%，实验测试得到的衰减系数显示出异常高值(金相分析发现有长度超过300μm的异常大孔隙存在)，此时，Martin模型对应的计算结果未显示衰减系数有“跟随性”的升高，但此时由随机孔隙模型得到的衰减系数却与实验值同步增加，这充分表明随机孔隙模型能够灵活跟踪、准确捕捉孔隙形貌变化及其对超声衰减的影响。

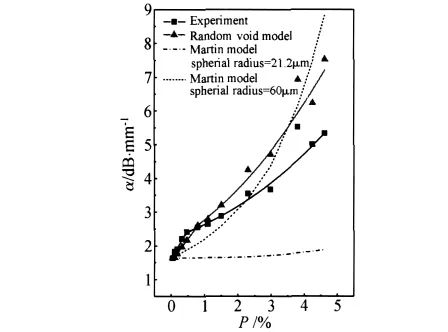
图4 超声衰减系数模型预测结果与实验结果比较(5MHz)Fig.4 Comparison of measured and theoretical ultrasonic attenuation coefficients using random void model and Martin model(at 5MHz)

4 分析与讨论

由上述比较可知，以Martin为代表提出的确定性模型将含孔隙复合材料看做各向同性均匀介质，假设孔隙形状规则、分布离散均匀，因此，对于给定的材料，在孔隙率确定的条件下，孔隙的形貌是固定不变的。随机孔隙模型依据随机介质理论，采取统计学原理和方法，将基体看做是大尺度上具有平均特性的背景介质，将孔隙看做是小尺度上的随机扰动，由此得到的随机孔隙模型能够得到与真实孔隙几何相似性良好的孔隙形貌。此外，随着孔隙率增加，基于此模型得到的超声衰减系数明显增加，模型预测结果和实验结果之间具有较好的一致性和跟随性。与传统的确定性模型相比，随机孔隙模型显示出较好的灵活性和适应性。同时，由随机孔隙模型构建原理可知，其还具有良好的“可塑性”，即，可以根据实际复合材料中孔隙形貌特征数据统计分析的结果对模型进行反复优化，使其更为准确地反映实际孔隙形貌。

利用随机孔隙模型能够解释经典的确定性孔隙模型无法解释的一些现象。例如，大量资料表明［16～18］，孔隙的存在会导致复合材料力学性能下降，众多研究结果从定性角度均取得很好的一致性，但定量结果却有很大差异。孔隙率每增加1%，不同报道给出的层间剪切强度下降的幅度在5%～15%之间变化［10］。又如，对于树脂传递模塑成型工艺或热压罐法等不同复合材料体系或加工方法，对于同样的孔隙率，复合材料性能差异却很大。以上现象产生的主要原因，即在于孔隙形貌特征的差异，即对于给定的材料，尽管孔隙率相同，但孔隙形状、尺寸、取向和分布等微观形貌特征的差异，导致含孔隙复合材料介质的局部密度、弹性模量等物理及力学性能的差别，宏观上即表现为复合材料力学性能数据具有明显的离散性。

5 结论

(1)随机孔隙模型适合于描述碳纤维增强复合材料中孔隙的几何形貌特征。

(2)孔隙率相同时，孔隙形貌的变化对超声波衰减系数产生影响。

(3)基于随机孔隙模型和有限差分法获得的超声波衰减系数的模拟结果与实验测量结果更为接近。

［1］JEONG H.Effects of voids on the mechanical strength and ultrasonic attenuation of laminated composites［J］.Journal of Composite Materials，1997，31(3):276-292.

［2］BIRT E A，SMITH R A，A review of NDE methods for porosity measurement in fibre-reinforced polymer composites［J］.Insight，2004，46(11):681-685.

［3］CASAL E，GRANDA M，BERMEJO J，et al.Influence of porosity on the apparent interlaminar shear strength of pitch based unidirectional C-C Composites［J］.Carbon，2001，39:73-82.

［4］HASHIN Z.The elastic moduli of heterogeneous materials［J］.J Appl Mech，1962，29(1):143-150.

［5］MARTIN B G.Ultrasonic attenuation due to voids in fiber reinforced plastic［J］.Non-destructive Testing International，1976，9(5):242-246.

［6］MARTIN B G.Ultrasonic wave propagation in fiber reinforced solids containing voids［J］.Journal of Applied Physics，1977，48(8):3368-3369.

［7］HALE J M，ASHTON J N.Ultrasonic attenuation in voided fiber reinforced plastics［J］.Non-destructive Testing International，1988，21(5):321-326.

［8］JEONG H，HSU D K.Experimental analysis of porosity induced ultrasonic attenuation and velocity change in carbon composites［J］.Ultrasonics，1995，33(3):195-203.

［9］周晓军，莫锦秋，游红武.碳纤维复合材料分布孔隙率的超声衰减检测方法［J］.复合材料学报，1997，14 (3):107-113.

［10］HUANG H S，TALREJA R.Effects of void geometry on elastic properties of unidirectional fiber rein-forced composites［J］.Composites Science and Technology，2005，65:1964-1981.

［11］LIN L，ZHANG X，CHEN J.A novel random void model and its application in predicting void content of composites based on ultrasonic attenuation coefficient［J］.Appl Phys A，DOI 10.1007/S00339-010-6061.

［12］牟云飞.基于随机孔隙模型的CFRP孔隙率超声检测研究［D］.大连:大连理工大学材料科学与工程学院，2009.

［13］IKELLE L T，YUNG S K，DAUBE F.2-D random media with ellipsoidal autocorrelation function［J］.Geophysics，1993，58(9):1359-1372

［14］牟云飞，张翔，林莉，等.基于随机孔隙模型的CFRP孔隙率超声检测研究［J］.机械工程学报，2010，46(4): 22-26.

［15］罗明.碳纤维增强树脂基复合材料孔隙率超声无损检测［D］.大连:大连理工大学材料科学与工程学院，2007.

［16］朱洪艳，李地红，张东兴，等.孔隙对纤维增强聚合物基复合材料层压板力学性能影响的研究进展［J］.中国机械工程，2009，20(13):1619-1624，1629.

［17］BOWLES K J，FRIMPONQ S.Void effects on the interlaminar shear strength of unidirectional graphite-fiber-reinforced composites［J］.Journal of Composite Materials，1992，26(10):1487-1509.

［18］OLIVIER P，COTTU J P，FERRET B.Effects of cure cycle pressure and voids on some mechanical properties of carbon/epoxy laminates［J］.Composites，1995，26 (7):509-515.