基于应力状态参数的韧性材料损伤机理研究

何 敏， 李付国

(1.西北工业大学材料科学与工程学院，西安710072;2.徐州工程学院机电工程学院，江苏徐州221008)

韧性材料的损伤断裂问题一直是航空材料成形研究中较被关注的问题之一。在损伤微观机理的研究方面，由于小范围的屈服断裂会有较多的不确定性因素影响裂纹的起裂和扩展准则，如加载速率，材料界面，微裂纹的尺寸和其他复杂环境等［1］，传统的基于应力强度因子的K和J积分的裂纹起裂与扩展准则适用性受到一定限制［2～4］。Barenblatt和Dudgale首次提出将材料微尺度下的断裂描述为沿一定表面的分离，裂纹尖端塑性区上下表面服从内聚力模型(Traction-Separation law)［5］。Needleman，Rice等也倡导将断裂视为材料在扩展裂纹前端或内聚区克服内聚力而逐渐分离的过程，当内聚区域内曲线裂纹前端张开位移出现峰值点时，材料将分离并产生微观断裂［6］，即对材料施加载荷，断裂的过程就是内聚元上下表面逐渐分离的过程。同时，细观损伤力学理论及部分试验研究也证明，韧性材料的裂纹大部分起始于材料内部脆性二次相的破裂与脱粘［7，8］。这些微观损伤在外力持续作用下不断扩展与聚合，最终形成韧性材料的宏观断裂，在二次相断裂的位置最终形成韧窝，较大二次相粒子可在韧窝处观察到。

已有较多的试验表明，材料断裂过程除与材料内秉特性有关外，还与其应力状态密切相关，加载方式影响裂纹萌生的形式。但由于研究尺度的限制，损伤的微观机理尚不明确。为研究损伤在不同载荷下的萌生机制，利用应力莫尔圆给出了9种应力状态组成的载荷谱，并在基于能量释放原理的内聚元模型基础上研究5052铝合金微观裂纹的萌生-开裂过程，同时采用显式的应力状态参数探讨裂纹萌生-扩展过程中应力场对材料塑性变形和断裂形式的影响。通过应力状态参数的变化来判断细观裂纹的萌生模式和扩展类型等特征，从而为材料断裂的细观扩展规律研究提供参考。

1 内聚元本构关系模型

内聚元模型采用能量破坏作为损伤准则，其每一单元拉伸破坏都可等效为一个分层扩展过程，内聚元损伤-开裂过程用牵引力-位移关系来描述，如图1所示。

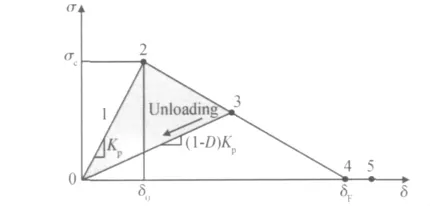
图1 内聚元牵引力-位移模型Fig.1 Traction-Separation law model in cohesive element

内聚元损伤准则反映了应力σ与裂纹尖端位移δ的关系。软化准则服从双线性模型，即当内聚区的承载达到损伤门槛值δ0后，内聚区材料的承载能力线性下降。对于I，II，III型裂纹，在界面正应力和剪应力达到各自的极限抗拉强度和极限抗剪强度后，材料刚度逐渐减少至0。应力-位移曲线所包络的面积即为断裂能(图中阴影部分所示)。用Rice提出的J积分理论描述内聚区域:

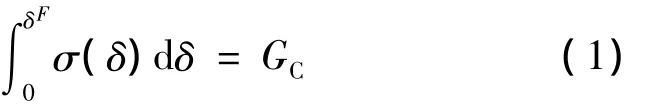
其中GC表示特定裂纹开裂模式下的能量释放率门槛值。

双线性关系求解内聚元软化关系。

①塑性区裂纹尖端位移小于损伤门槛值时，即δ＜δ0:

σ=KPδ;

②δ0＜δ＜δF:

σ=(1-D)KPδ，

其中D表示内聚元内的损伤累积变量，起始值为0，当该值渐变至1时，材料完全失去承载能量，发生破坏;

③δ＞δF:所有的罚刚度都等于0，出现裂纹闭合情况时，在内聚元本构模型中，需要定义起始罚刚度KP，断裂能GIC，GIIC，GIIIC及相应的名义抗拉强度T，抗剪强度S。

当内聚元能量释放量达到损伤能量门槛值后，材料出现局部微损伤，之后内聚元进入软化阶段，其表现为刚度弱化系数(SDEG)逐渐下降。当微观损伤发生以后，断裂面的自接触遵从法向罚函数刚度法则。即当断裂面出现面面渗透时，罚函数法作为求解面面接触的定解条件。同时，不考虑摩擦效应［9，10］。

韧性材料的断裂过程包括了孔洞的萌生，扩展，聚合三个阶段。在孔洞萌生阶段，大部分的孔洞来源于二次相粒子和夹杂，出于材料增强的目的，二次相往往比基体硬、脆。将二次相定义为内聚元，由于韧性材料中二次相在微米尺度，相应定义脆性层的厚度为微米级，并用脆性相的应力-应变弹性本构矩阵来初始化内聚元的弹性状态［7］。tn表示沿界面法向的拉伸应力矢量;ts，tt分别为沿界面切向的两个拉伸应力矢量，与此对应的位移分别为δn，δs，δt。定义脆性层厚度为T0，各应变量为:

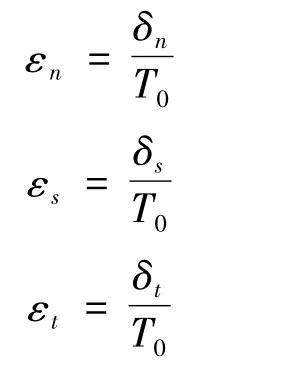
因此，脆性相的应力-应变弹性本构关系表达如下:

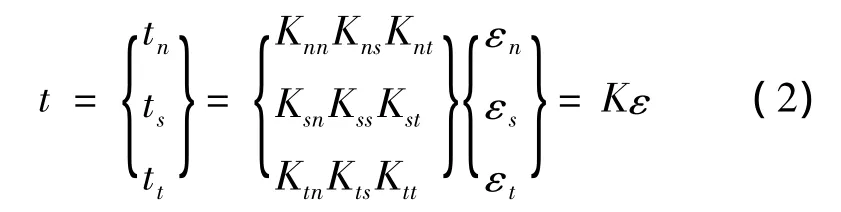
式中，K为刚度系数。

2 数值计算

2.1 有限元模型

以微观视场中长10μm正方形区域作为分析模型范围，在模型中心预置长椭圆形二次脆性相，有限元模型如图2所示。

图2 含二次脆性相韧性材料的视场有限元模型Fig.2 Finite element model containing the inclusion

基体为5052铝合金，主要成分及力学性能如表1，表2所示。

表15052 铝合金化学成分(质量分数/%)Table 1 Chemical composition of 5052 aluminum alloy(mass fraction/%)

表2 5052铝合金基本力学性能Table 2 Mechanical properties of 5052 aluminum alloy

二次相主要成分为Al2O3，基于纳米压痕试验方法利用岛津MCT-W501型微小材料试验机获得Al2O3加卸载曲线，根据Oliver-Pharr法计算Al2O3颗粒弹性模量［11，12］，如式(3)，(4)所示:

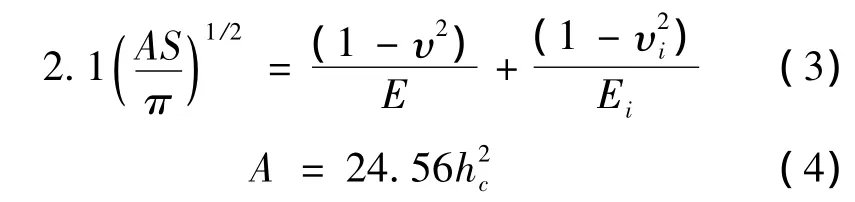
式中，Ei，υi分别为压头的弹性模量与泊松比;E，υ分别为被测材料的弹性模量与泊松比，S为卸载刚度。试验机使用金刚石锥型压头，压头的弹性模量Ei=1141GPa，泊松比υi=0.07。计算得出弹性模量为420GPa，其断裂能为210J/m2。

2.2 表征应力状态的载荷工况

对于薄板成形而言，在沿厚度方向的应力为零或者较小时，认为是平面应力状态。其应力状态用两个方向上的主应力来表示，共有以下4种状态:拉-拉，拉-压，压-压，压-拉。在塑性变形过程中，当材料质点满足屈服准则时即开始发生塑性变形。板料成形主应力表达式如式(5)所示:

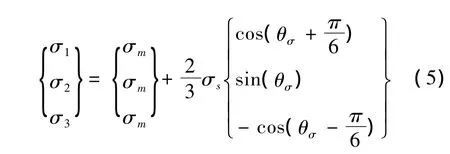
表3 板料成形的应力状态Table 3 Stress conditions of sheet mental forming

为使板料承受表3主应力，现分别在有限元模型 中施加X轴和Y轴等效应力σx，σy，见表4所示。

3 结果与讨论

应力状态参数与金属材料损伤与断裂存在一定的关系［13］。当脆性相受载时，裂纹尖端塑性区的应力状态发生变化，脆性相与基体材料内产生的塑性变形与应力集中程度随之改变，材料损伤断裂机理发生变化［14］。现采用应力状态参数中的三个量:应力三轴度Rd、应力状态软性系数α和罗德参数μd来表征板料受载形变后微观区域的应力状态:

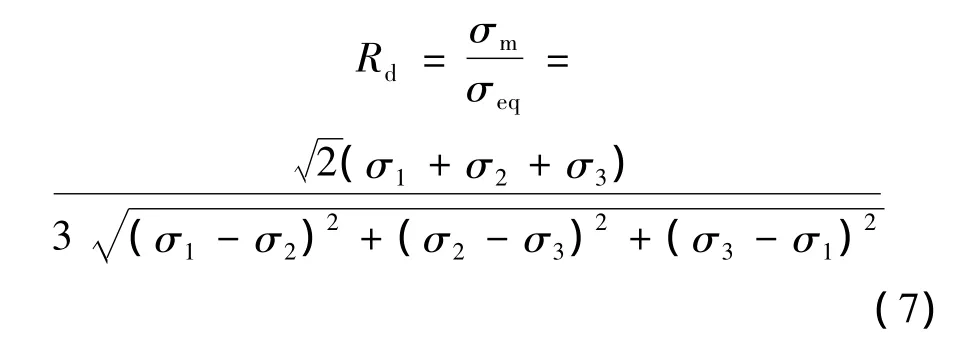
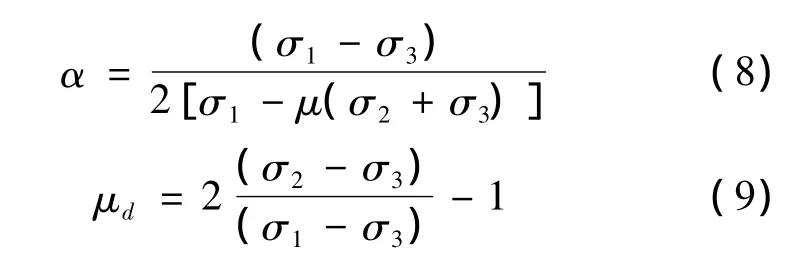
式中，σm，σeq分别表示平均应力和等效应力，μ为泊松比。

3.1 应力状态参数

在ABAQUS计算模型基础上，采用用户自定义子程序UVARM输出应力状态参数作为场变量，不同加载条件下各应力状态参数的等值线见图3所示。图a～d，e～h，i～l，m～p，q～t分别代表应力状态为单向拉伸，单向压缩，双向拉伸，双向压缩，纯剪切加载区域应力状态参数。

图3 不同加载条件下应力状态参数等值线 (a～d)单向拉伸;(e～h)单向压缩;(i～e)双向拉伸; (m～p)双向压缩;(q～t)纯剪切Fig.3 Stress state parameter contours on various loading mode (a～d)uniaxial tension;(e～h)uniaxial compression; (i～l)biaxial tension;(m～p)biaxial compression;(q～t)pure shear

3.2 分析讨论

应力三轴度Rd表征应力状态，Rd＞0时是以拉为主的应力状态，板料变形特征为厚度减薄;Rd＜0时是以压为主的应力状态，板料变形特征为厚度增厚;Rd=0时为纯剪切应力状态，此时板料厚度不变［15］。在微观机理方面，Rd代表材料内空穴韧窝机制的发展相对剪切机制发展的优势，当应力三轴度高时，材料内韧窝机制占优，空穴扩张较快，尽管剪切机制可能也有相当的发展，但材料的宏观表现为韧窝型;当应力三轴度较低而剪切应变高时，剪切机制占优［16］。

应力状态软性系数α反映应力状态的软、硬程度，α值越大材料中剪应力分量越大;反之，软性系数α越小。材料中正应力分量越大，应力状态越硬，材料越不易产生塑性变形，而易于产生脆性断裂［17］。

罗德参数μd表征材料的变形模式，并且决定了应变增量的比值，可从机理上反映构件的应变状态，其变化范围为-1≤μd≤1。μd决定了应变增量的比值。

SDEG的值表征材料刚度的变化情况，损伤起始于单元内部刚度最先衰减的位置。

①单向拉伸和广义拉伸

单向拉伸载荷下椭圆形脆性相粒子形变后应力三轴度，应力状态软性系数，罗德参数分布如图3a～d所示。从应力三轴度分布云图:基体材料Rd＞0，表现为宏观上受拉;脆性相应力三轴度由外向内逐渐降低，在中部Rd＜0受压应力作用。在软性系数云图中代表脆性相的内聚元内软性系数值最大，且均大于1，则平行于裂纹面并且垂直于裂纹前缘的剪应力是裂纹产生的主要动力，材料的韧性和塑性较大，产生的裂纹以II型裂纹为主。从罗德参数的分布可判断内聚元与基体变形不协调，内聚元基本处于μd＞0产生压缩类应变，基体部分μd＜0产生伸长类应变［18，19］。由于内聚元受压方向与自身的位形方向存在一定的偏心，内聚元压缩后在切应力的作用下率先出现断裂。因此，处于图示位相的椭圆形脆性相粒子起裂位置沿椭圆短轴，并在压应力作用下被切断萌生微观损伤，属于II型裂纹。

广义拉伸的加载方式与单向拉伸有相同的裂纹萌生机制，由于Y轴方向受压，相当于加强X轴方向受拉的作用程度，与单向拉伸相比更容易在较小的作用力下萌生裂纹。短轴方向的压应力对裂纹的萌生起到了促进作用。因此，切应力的作用更明显，裂纹将在椭圆体内部萌生，断裂方式为II型。

含椭圆形脆性二次相单轴拉伸后裂纹萌生的SEM照片如图4所示。

图4 椭圆形脆性二次相开裂微观组织Fig.4 Microstructure of cracked elliptic inclusions

将理论分析结果与试验结果比较，微观裂纹的起始路径与理论计算较为吻合。

②单向压缩和广义压缩

单向压缩载荷下椭圆形脆性二次相形变后应力三轴度，应力状态软性系数，罗德参数分布示于图3e～h，与单向拉伸类型的应力状态呈现相反的规律。在应力三轴度等值线图中，基体材料Rd＜0主要受压应力作用，即宏观上表现为受压。而在微观上脆性相椭圆长轴顶部和中间部分区域Rd＞0承受一定的拉应力作用。并在长轴顶部的脆性相与基体界面处的应力三轴度出现最大值。在软性系数等值线图中，基体的软性系数值较大，为1.3～1.5;内聚元内软性系数值较小，其值为0.5～0.7，表明脆性相中最大正应力分量较大，切应力分量小，应力状态“硬”。从罗德参数可以看出内聚元与基体变形的不协调，内聚元μd＜0产生伸长类应变，基体部分处于μd＞0产生压缩类应变。单向压缩加载条件下，裂纹出现在椭圆短轴处，为与基体脱粘的I型裂纹。

广义压缩其应力状态与单向压缩有相同之处，由于Y轴方向受拉，相当于加强了X轴方向的受压作用程度，与单向压缩相比更容易在较小的作用力下萌生裂纹。Y轴方向的拉应力对裂纹的萌生起到了促进作用。因此，脱粘作用更明显。

③双向拉伸和双向等拉

双向拉伸应力状态分布如图3i～l所示。而双向等拉的应力状态分布与双向拉伸相似。刚度在结合界面处首先衰减，脆性相与基体结合面的Rd＞0，受拉。α＜1，以正应力为主。罗德参数亦在脆性与基体的结合界面上出现负值，即脆性相在双向拉伸载荷下将沿椭圆长轴面以与基体脱粘的方式出现裂纹，裂纹类型为I型。

而相比于单向拉伸，同等载荷条件下双向拉伸的刚度弱化系数值更大，证明双向拉伸的加载方式更容易萌生微裂纹。

④双向压缩和双向等压

双向压缩和双向等压应力状态分布类似，如图3m～p所示。基体材料Rd＜0，宏观上受压应力作用，微观脆性相Rd＞0，局部受拉应力作用。基体材料和脆性相内部α＜1，而在脆性相与基体的界面上α＞1且达到最大值，其值呈现由小变大再增大的趋势。罗德参数从基体的较大值逐渐减小，亦在脆性与基体的结合界面上出现负值，在出现最小值后，沿脆性相心部方向逐渐增大，在基体与脆性相界面处有明显的应力状态差异，出现沿界面脱粘的特征。即脆性相在双向压缩载荷下沿椭圆长轴面以与基体脱粘的方式出现裂纹，裂纹类型为I型。刚度还未出现弱化，在同等条件下双向等压是最不易诱发二次相微观裂纹的加载变形方式。

⑤纯剪切

由于X，Y轴方向上的载荷相同，拉应力和压应力同时占据主导作用，应力状态较为复杂，如图3q～t所示。综合了Ⅰ，Ⅱ型的应力状态特征，为Ⅰ，Ⅱ混合型裂纹。裂纹起始部位也较多，所需应力较小，是一种最容易诱发裂纹萌生的加载方式。

4 结论

本工作采用内聚元模型研究了微观尺度下椭圆形脆性二次相在不同加载方式下的裂纹萌生机制和裂纹类型，基于微观性能定义的内聚元在计算微米尺度下二次相粒子损伤开裂过程中具有较强的适用性。在米赛斯屈服准则与屈雷斯加屈服准则统一的载荷谱基础上，通过用户定义子程序，以数值显示的形式探讨应力状态参数与微观裂纹萌生方式和裂纹类型的关系，并通过刚度弱化系数判断损伤起始点，用应力状态参数预测裂纹类型。为微观，局部的损伤萌生研究奠定基础。

(1)当材料受载时，脆性相及脆性相周围塑性区的应力状态发生变化，脆性相的应力状态与远离脆性相区域的应力状态存在不均匀性，这种应力状态的不均匀性是致使裂纹萌生的主要原因。

(2)不同应力加载方式萌生不同类型裂纹:单向拉伸和广义拉伸易于萌生II型裂纹;单向压缩和广义剪切易于萌生I型裂纹;双向拉伸和双向等压更容易萌生I型裂纹。单向压缩易于萌生Ⅱ型裂纹。纯剪切加载方式易于萌生混合型裂纹。

通过各加载方式下应力状态参数的分布，深入了解韧性材料于塑性加载下的微观损伤机制。本工作提供的研究方法和结论亦可推广到其他形态和位相的二次相微裂纹、微损伤的研究工作中，也可为材料微塑性成形加工中损伤断裂的细观规律研究提供参考。

［1］ORTIZ M，PANDOLFI A.用于三维裂纹扩展分析的有限变形不可逆内聚元［J］.力学进展，2008，38:630-639.

［2］CORNEC Alfred，SCHEIDER Ingo，SCHWALBE Karl-Heinz.On the practical application of the cohesive model［J］.Engineering Fracture Mechanics，2003，70(14): 1963-1987.

［3］MASHAYEKHI M，ZIAEI-RAD S，PARVIZIAN J，et al. Ductile crack growth based on damage criterion:Experimental and numerical studies［J］.Mechanics of Materials，2007，39(7):623-636.

［4］汤安民，刘天鹏.韧性材料断裂形式与J准则存在的问题［J］.机械强度.2004，26(6):199-201.

［5］BARENBLATT G I.The mathematical theory of equilibrium cracks in brittle fracture［J］.Advanced Application Mechanics，1962，7(6):55-129.

［6］NEEDLEMAN A.Continuum model for void nucleation by inclusion debonding［J］.Journal of Applied Mechanics，1987，54(3):525-531.

［7］朱知寿，马济民，高扬，等.富Nd第二相颗粒对钛合金拉伸断裂方式的影响［J］.航空材料学报，2000，20(3):27 -32.

［8］BESTERCI Michal，IVAN Jozef，PESEK Ladislav，et al. Damage mechanism of Al-12Al4C3［J］.Meterials letters，2004，58(6):867-870.

［9］DÁVILA C G，CAMANHO P P，MOURA M F De.Mixedmode decohesion elements for analyses of progressive delamination［C］∥42nd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference. Seattle，Washington，April 16～19，2001.

［10］WANG Zhi-qiang，NAKAMURA Toshio.Simulations of crack propagation in elastic-plastic graded materials［J］. Mechanics of Materials，2004，36(7):601–622.

［11］OLIVER W C，PHARR G M，Improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments［J］.Journal of Materials Research，1992，7(6):1564-1580.

［12］王凤江，钱乙余，马鑫.纳米压痕法测量Sn-Ag-Cu无铅钎料BGA焊点的力学性能参数［J］.金属学报，2005，41(7):775-779.

［13］马凯，李智慧，汤安民.金属材料断裂与应力状态参数的关系［J］.西安理工大学学报，2007，23(2):201-204.

［14］NARAYANASAMY.R，RAVINDRAN C R.Analysis of fracture limit curves and void coalescence in high strength interstitial free steel sheets formed under different stress conditions［J］.Journal of Materials Science，2008，43 (9):3351-3363.

［15］KIM Jinkook，GAO Xiao-sheng，SRIVATSAN Tirumalai. Modeling of void growth in ductile solids effects of stress triaxiality and initial porosity［J］.Engineering Fracture Mechanics，2004，71(6):379-400.

［16］BAO Ying-bin，TOMASZ Wicrzbicki.On fracture locus in the equivalent strain and stress triaxiality space［J］.International Journal of Mechanical Sicine，2004，46(7):81 -98.

［17］ZHU Hao，ZHU Liang，CHEN Jian-hong，et al.Investigation of fracture mechanism of 6063 aluminum alloy under different stress states［J］.International Journal of Fracture，2007，146(3):159-172.

［18］苑世剑，李峰，何祝斌.塑性变形类型与罗德系数的关系［J］.哈尔滨工业大学学报，2008，40(1):61-64.

［19］王仲仁.Lode参数的物理实质及其对塑性流动的影响［J］.固体力学学报，2006，27(3):277-282.