基于变位方法的无底大圆筒结构稳定性研究
宋少沪,马兰,姚文娟
(上海大学土木工程系,上海 200072)
1 引言
沉入式大圆筒结构是大圆筒结构形式中最具特色的一种,与经典的重力式水工结构相比,它不需要很强的持力层,尤其对于淤泥质软土地基,它无需拋石基床,并可避免开挖地基,这些不可替代的优势使它广泛地应用在水运水利工程中。但由于该结构的工作机理不同于经典的水工结构,使其计算分析模型仍处于探索中,国内外学者对此进行了研究。刘建起[1]在忽略了竖向和水平位移后,提出了大圆筒转动高度的计算方法;王元战等人[2]提出了一种沉入式无底大圆筒结构与土相互作用的分析模型,该模型可以求出大圆筒的变位,2002年他又将大圆筒分为重力式和桩墙式[3],提出了一种稳定的分析方法;范庆来等人[4,5]对于横观各向同性软土地基上的沉入式大圆筒提出了一种准三维上限分析方法,证实了大圆筒的破坏是围绕中轴线上的某点;同年,王乐芹等人[6],建立了大圆筒结构的上限法极限分析模型,得到大圆筒上的横向极限荷载。对于大圆筒的临界变位值,刘建起[7]通过实验,得出了在转角为0.2°时,圆筒的抗倾能力最强。到目前为止,反映沉入式大圆筒工作性状,既考虑水平位移及竖向位移,同时又考虑倾覆转动点高度的稳定计算模型尚未见报道。基于此,本文提出一个改进的稳定计算模型,通过算例计算分析,与传统方法、有限元方法进行比较,验证了本文方法的正确性。
2 受力模型
受力分析模型图如图1所示,假设圆筒的转动点距离筒顶高hu,hu为与各种参数相关的量,圆筒的水平位移为u,竖直位移为v,转角为θ。圆筒失稳过程为从C点运动到 C′。
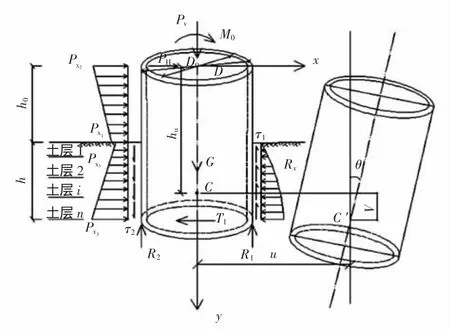
图1 分析模型
3 外荷载及反力
3.1 外荷载
筒体顶部作用有水平荷载PH,竖向荷载PV,弯矩M0,沿纵向作用有波浪分布荷载Px0、Px1。
3.2 土体对结构的作用力
3.2.1 深度为y处土的抗力
假设水平地基系数kx随深度线性增大,其比例系数为p,根据温克尔假定,在深度为y处土体抗力为:
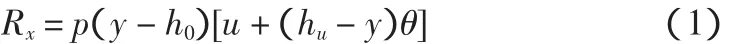
3.2.2 地基对筒底反力
假设地基对筒底面某点的反力与该点竖向位移成正比,竖向地基系数为:
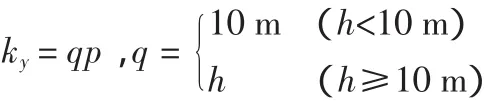
根据上述假定,竖向地基反力为:
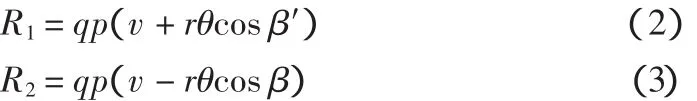
3.2.3 地基对筒底水平切力
假设圆筒底面同地基土的水平切力与筒底水平位移u呈线性关系。则筒底面总切力为:

3.2.4 土体对筒壁的竖向切力
假设土体竖向剪切刚度系数kv与土体水平作用力成正比,及kv=λfx,圆筒与土之间的竖向剪切刚度系数kv=λp(y-h0)[u+(hu-y)θ]。与轴线垂直方向成 β′角的筒前土体竖向切力为:
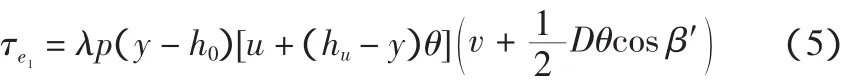
筒前沿环向单位宽度的总纵向切力为:
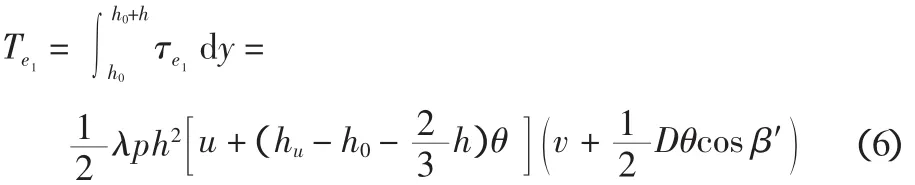
筒后沿环向单位宽度总的纵向切力为:
4 方程推导
4.1 水平方向平衡
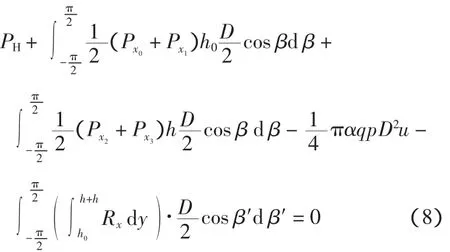
简化后为:
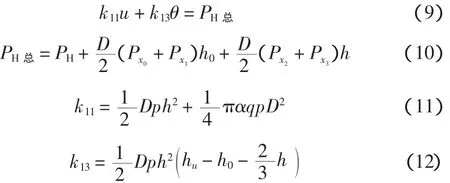
4.2 竖直方向

简化后为:
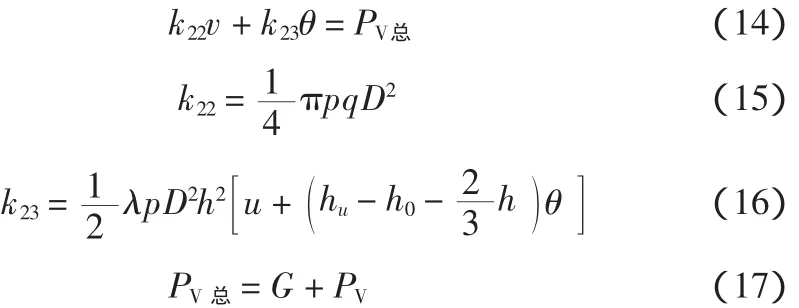
4.3 各种力产生的弯矩
(1)墙前竖向切力产生的弯矩
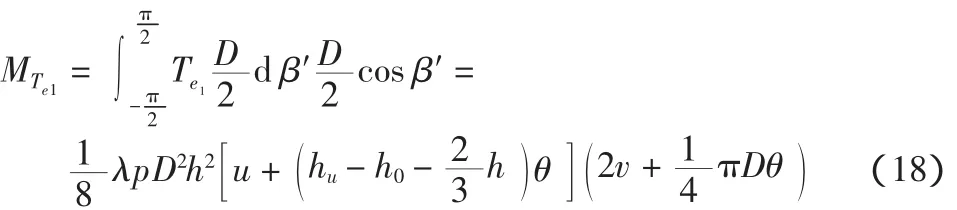
(2)墙后竖向切力产生的弯矩
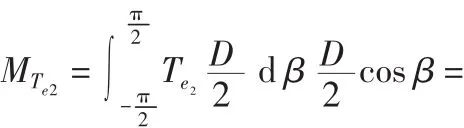
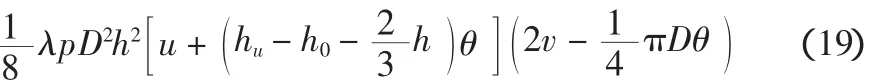
(3)Rx产生的弯矩
①hu以上的部分
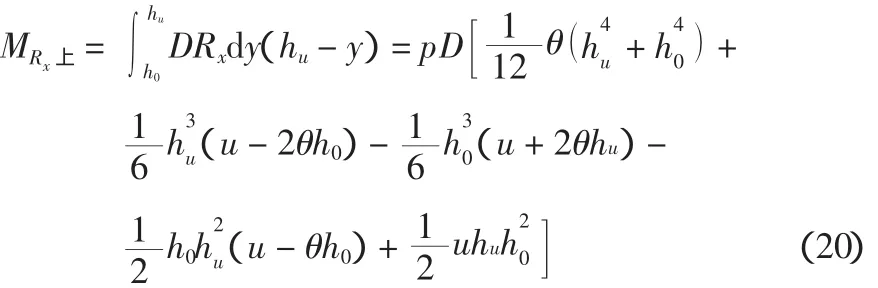
②hu以下部分
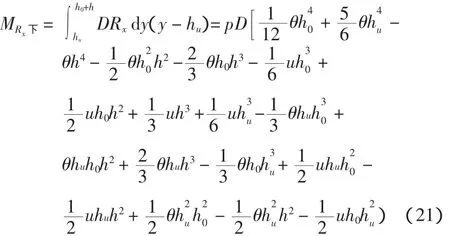
(4)波浪力Px0-Px1产生的弯矩
沿深度方向任意深度的波浪力:
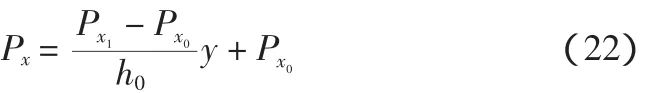
Px产生的弯矩:
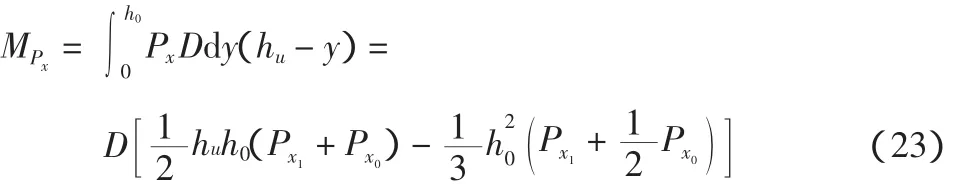
(5)土压力Px2-Px3产生的弯矩
沿深度方向任意深度土压力:
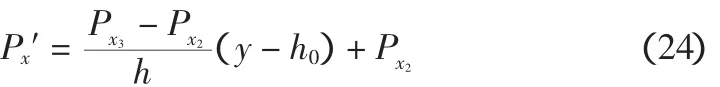
①hu以上产生的弯矩
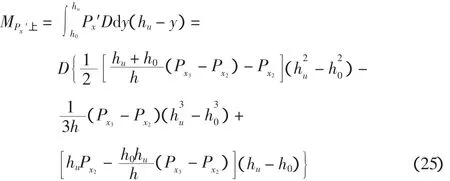
②hu以下产生的弯矩
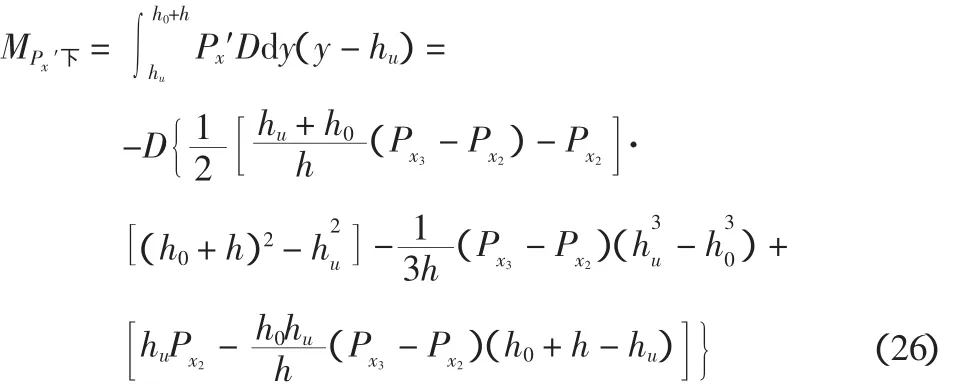
(6)底部反力弯矩
①底部靠近筒前趾一侧R1产生的弯矩
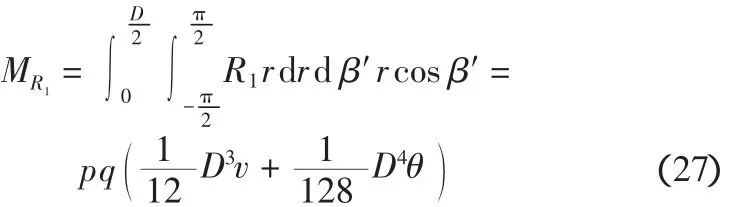
②底部靠近筒后趾一侧R2产生的弯矩
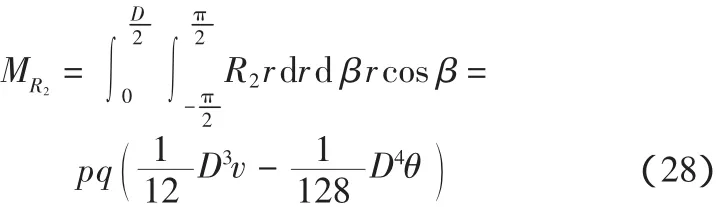
③底部切力弯矩
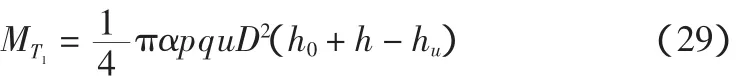
对转动点C′取弯矩
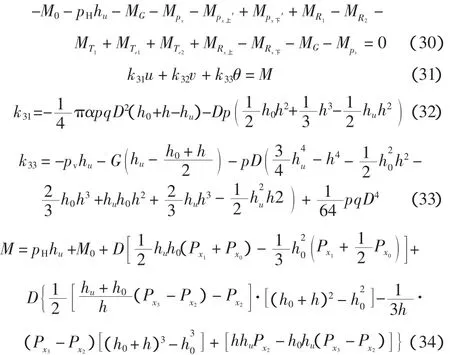
求解由(9)、(14)、(31)组成的方程组,程序流程见图2。
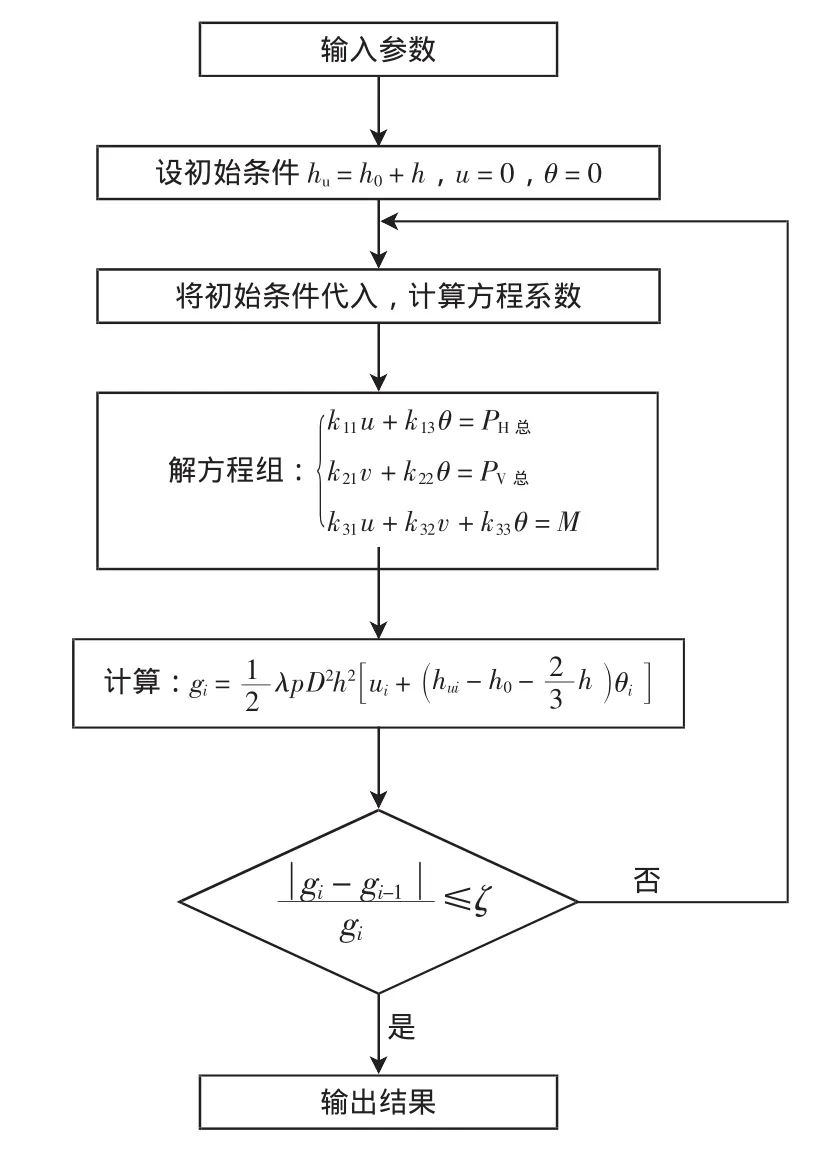
图2 程序流程图
方程系数中含有未知量,该方程为一非线性方程组,利用迭代法进行求解。方程中具体参数取值为p=1 000 kN/m4,α=0.122,λ=0.117。(α:地基水平剪切系数与竖向地基系数之比;λ:土体竖向剪切刚度系数与土体水平作用力之比)。
5 算例和分析
我国某深水航道的导堤建筑物为沉入式大圆筒结构。圆筒直径12.0m,筒顶标高-1.5m,筒底标高-23.5m,圆筒入土深度15 m。筒底以上13.2m长度范围壁厚为21 cm,筒顶以下7.0m长度范围内壁厚为25 cm,其间筒壁厚由21 cm渐变至25 cm,筒体单件重470 t。波浪要素为50 a一遇,T=8.01 s,当极端高水位5.11m时,其H1%=8.19m。
通过计算得到转动点高度为17.22m。下面计算了不同参数对转动点高度的影响,假设转动点高度hu与大直径圆筒的整个高度之比为无量纲参数η。
由图3~图6可知,大直径圆筒结构在破坏时,中轴线上存在转动点,这与传统计算模型以筒底为转动点破坏模式不同。当其他因素不变时,大直径圆筒的转动点高度随埋深增加而呈现向下移动的趋势;当埋深不变时,转动点高度随自由端高度的增加而呈现向上移动趋势。从无量纲参数与埋深的变化曲线可知,埋深的增加使无量纲参数减小,在埋深较小时,无量纲参数较大。由曲线可知,如果埋深足够小,转动点可能无限接近大直径圆筒筒底,该结论也与浅埋式圆筒采用筒底为转动点的破坏模型相符。由无量纲参数随自由端高度变化图可知,自由端高度的增加使无量纲参数增大。大直径圆筒的转动高度受直径的影响较小。
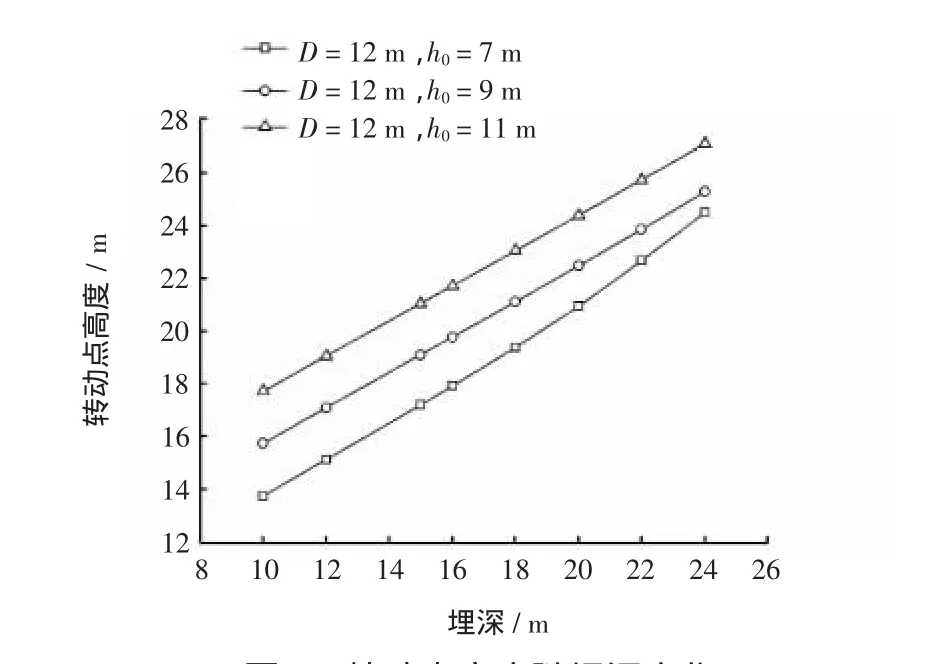
图3 转动点高度随埋深变化
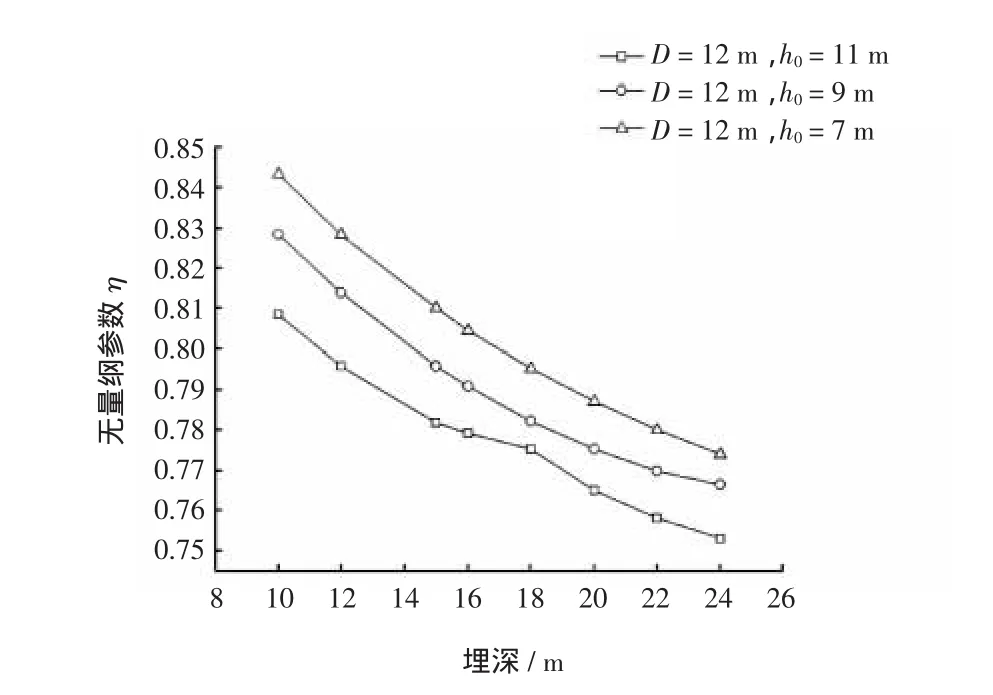
图4 无量纲参数随埋深变化
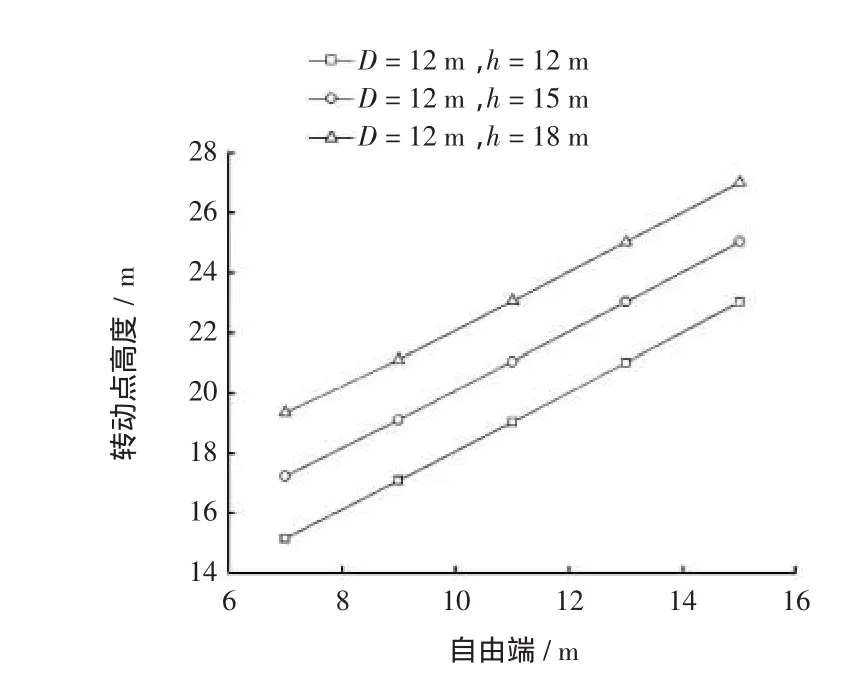
图5 转动点高度随自由端变化
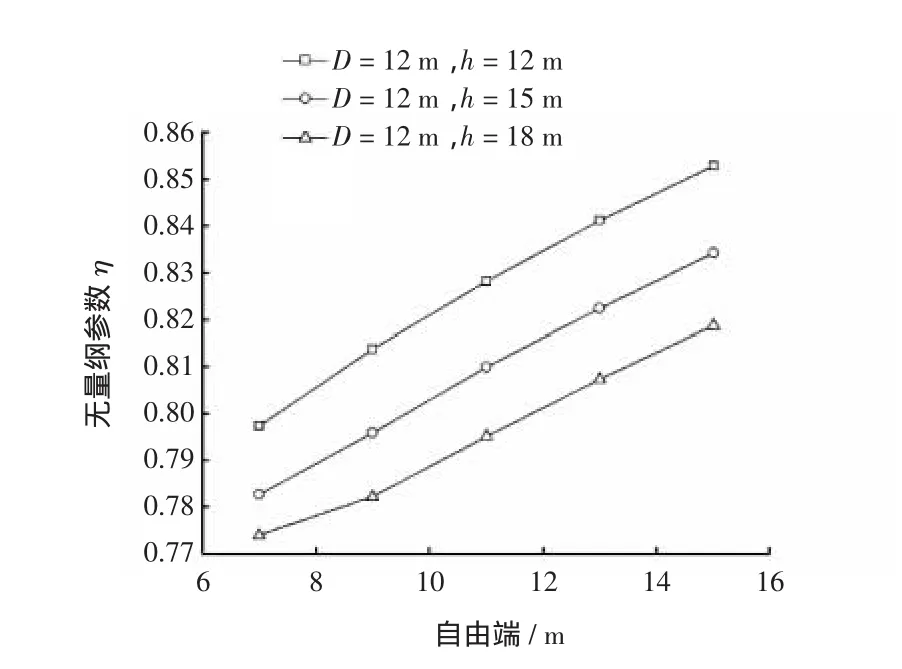
图6 无量纲参数随自由端变化
此外,利用该程序计算了不同荷载,不同参数对转动点高度的影响,结果表明这些参数对大直径圆筒的影响很小,由此可知大直径圆筒的转动高度主要受几何尺寸,尤其是沉入深度影响。
在本文算例所提供的工况下,计算了不同埋深下筒顶水平位移、竖向位移和转角,并且与文献 [2]模型计算结果、有限元计算的结果进行了对比。有限元采用大型通用软件ANSYS,大直径圆筒和土体采用实体单元solid45,土体采用非线性弹塑性体,土体平面长度和宽度方向上均取5倍的大圆筒直径,沿深度方向取2倍的埋深,筒内土体与大直径圆筒内壁以及筒外土体和大直径圆筒外壁之间均设有接触单元,建立三维模型。不同方法的计算结果如图7~图9。
由位移以及转动点随埋深变化图可知,以大直径圆筒筒底为转动点模型的计算结果是偏小的,有限元计算的结果与本文计算结果比较接近。本文模型与文献 [2]模型得出的位移差值、转角差值随埋深的增加而逐渐增加。在实际工程中,大圆筒的设计是以筒底为转动点来设计的。在埋深为15m时,文献 [2]计算水平位移结果为0.348m,而实际工程在埋深为15m时,水平位移大于此结果,大圆筒已经倾覆破坏(该结论与实际工程的失稳破坏一致)。由于工程设计中采用了传统计算模型,导致计算与实际的不吻合。
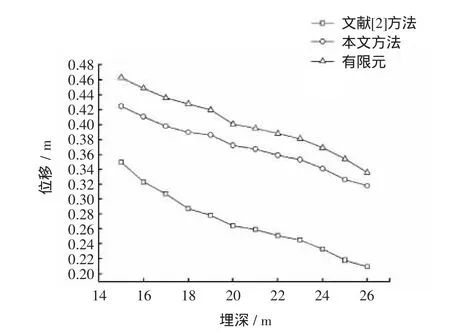
图7 不同方法的筒顶水平位移比较
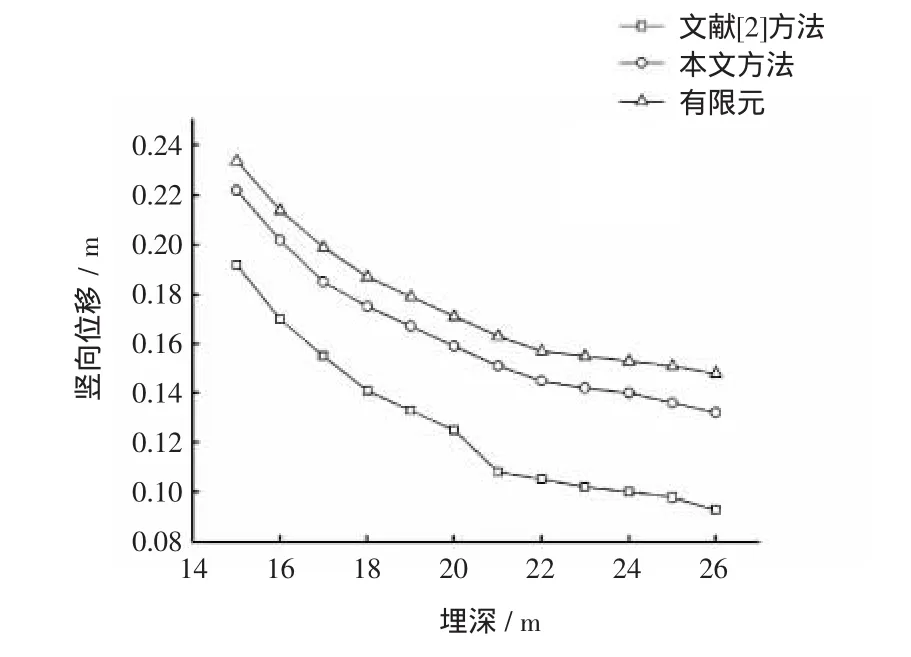
图8 不同方法的筒顶竖向位移
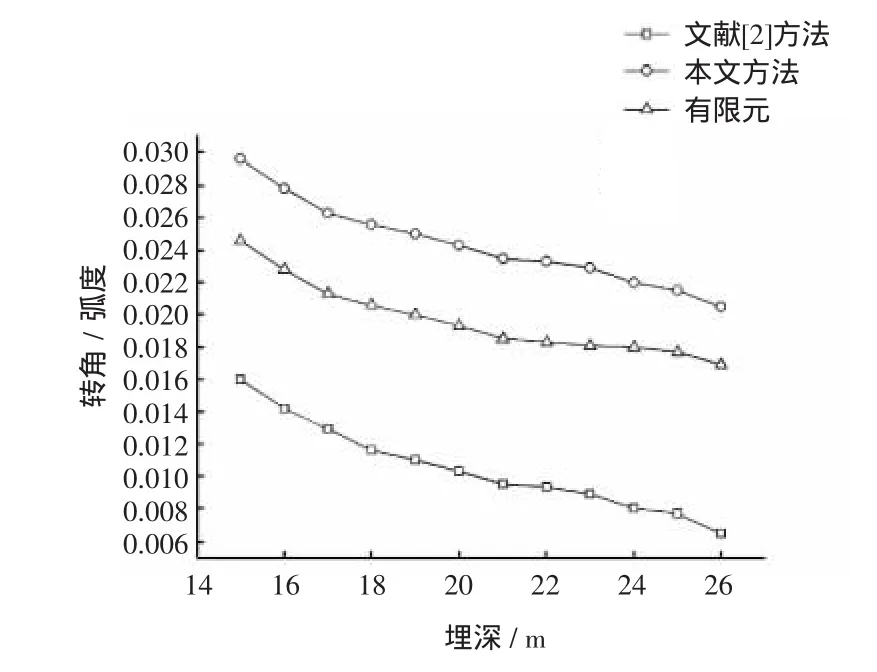
图9 不同方法的转角比较
6 结论
本文的稳定计算模型是大圆筒倾覆过程中围绕中轴线上某点转动,结果表明,转动点高度一般位于筒底以上(0.15~0.25)倍大圆筒筒高处。本文模型计算结果证实了大直径圆筒的转动高度主要受埋深和自由端高度的影响,其他因素对转动高度影响很小。
改进后的模型与传统模型计算的位移差异较大。转动点的上升导致负位移增大,基底拉应力增大,因此,传统的以筒底为转动点的稳定计算方法其位移计算结果不符合实际。因此导致一些已建的按传统方法设计的实际工程产生失稳破坏。
本文的稳定计算模型从一方面改进了传统水工结构稳定计算模型用于无底大圆筒结构的不足,从而为无底大圆筒结构的稳定分析提供参考并为实际工程的设计提供新的依据。
[1] 刘建起.沉入式大圆筒结构变形计算的实验研究[J].岩土工程学报,1994,10(2):64-72.
[2] 王元战,迟丽华.沉入式圆筒结构与土相互作用的模式及位移计算方法[J].土木工程学报,1997,30(2):68-73.
[3] WANG Yuan-zhan,ZHU Zhen-yu.An Approach to Stability Analysis of Embedded Large-Diameter Cylinder Quay[J].China Ocean Engineering,2002,16(3):383-393.
[4] 范庆来,魏峰先,陈彦明.横观各向同性软土地基上大圆筒防波堤稳定性研究[J].岩土工程技术,2005,19(6):287-291.
[5] LUAN Mao-tian,FAN Qing-lai.Numerical Analyses of Bearing Capacity of Deep-Embedded Large-Diameter Cylindrical Structure on Soft Ground Against Lateral Loads[J].China Ocean Engineering,2006,20(4):623-634.
[6] 王乐芹,周锡礽,张伟.软粘土中插入式大直径薄壁圆筒结构的一种极限状态分析模型[J].海洋技术,2005,24(1):95-100.
[7] 刘建起,左大伟,王敬莎.沉入式圆筒结构变位临界值及变位计算[J].天津大学学报,2006,39(2):170-175.

