环肋圆柱壳应力计算的新方法探索

王小明 陈节贵

1中国舰船研究设计中心，湖北 武汉 430064

2中国舰船研究院，北京 100192

环肋圆柱壳应力计算的新方法探索

王小明1陈节贵2

1中国舰船研究设计中心，湖北 武汉 430064

2中国舰船研究院，北京 100192

基于对目前环肋圆柱壳应力计算方法缺陷的认识，文中引入了加强棱柱壳体法，推导出环肋圆柱壳静力微分方程，通过将位移以傅立叶级数的形式展开，求出了环肋圆柱壳的位移解，进而得到环肋圆柱壳的应力解。通过算例计算表明，除环肋圆柱壳内表面纵向应力和肋骨周向应力外，用该方法的计算结果与传统方法的计算结果和有限元法结果都相接近，并且纵向应力与周向应力由外到里的变化规律与传统方法也相同。

环肋圆柱壳；应力计算；加强棱柱壳体法

1 引言

柱形壳体结构强度好，耗材省，易于加工，结构简单，且具有良好的水动力学性能，因而广泛应用于水工和船舶结构物上。潜艇耐压壳是环肋圆柱壳，是非常典型的柱形壳体结构之一。对于环肋圆柱壳的应力计算，传统的方法是将其处理成一维弹性基础梁［1-2］，这种方法实质上是假定环肋的形心与壳板重合，环肋的全部面积都集中在壳板的中面上，所以无论是内肋骨还是外肋骨，无论肋骨腹板的高与低，只要肋骨面积相同，其结果都一样，这种不考虑肋骨形心的偏离影响及内外肋骨差异的结构分析方法显然是不合理的［3］。在计算机技术高速发展的今天，有限元数值计算已经成为结构分析的有力工具，几乎可以用于计算任何的结构，但是它也存在一定的缺点：其一，数据准备困难，对于大型的复杂结构，建立有限元模型需要耗费大量的人力，且一旦结构设计需要修改，有限元模型修改就很困难，又需要重新建立模型，非常繁琐；其二，精度与时间的矛盾，有限元法原则上是单元离散得越小，计算精度越高，计算耗时也就会成比例增加。

基于对现存环肋圆柱壳应力计算方法各种缺陷的认识，本文引入一种名为“加强棱柱壳体法”的计算方法［4-6］，推导其在两端简支环肋圆柱壳应力计算中的计算公式，用于计算一算例，并与传统计算方法和有限元法比较。

2 基本假设和定义坐标系

加强棱柱壳体法的推导基于以下基本假设：

1）薄壳假设，厚度与壳半径a相比是小量，t／a＜＜1／20；

2）小变形假设，壳体位移与其厚度相比是一小量；

3）直线法假设，薄壳变形前垂直于中面的直线变形后仍为直线，且垂直于中面，z向的应变εz＝ 0；

4）中面法线方向上的应力与其他方向上的应力相比可以忽略，即σz＝0；

5）壳体材料是弹性的，各向同性；

6）采用唐纳尔（Donell）假设，忽略中面位移u、v对壳体曲率的改变及扭转改变的影响。在壳体中面内力平衡方程中（x向，y向），忽略中面外横向剪力 Qx、Qφ的影响。

对柱壳建立如图1所示坐标系。x轴沿壳体中面母线方向，y轴沿壳体中面的子线方向，y轴也可以用角度来度量，y=a φ，z轴沿壳体中面径向，以背离圆心为正。

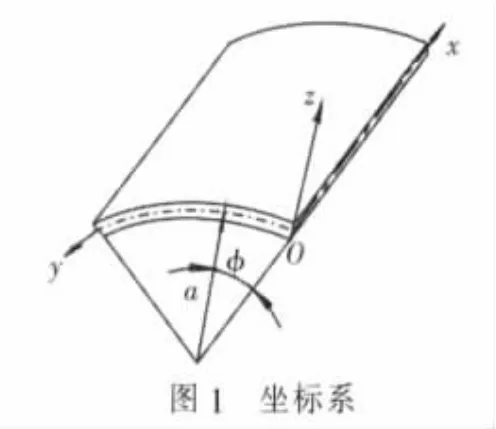
3 柱形薄壳的静力微分方程

由于壳体的中面在变形前就存在曲率，因此壳体内的位移、应变、曲率的改变和内力等基本量之间的关系是比较复杂的［7］。

取壳体微元adφdx为研究对象，薄壳中应力的合力和合力矩是内力，内力是单位长度上的力。内力包括轴向力N和周向力Nφ、周向剪力Nxφ和Nφx、弯矩 Mx，Mφ以及扭矩 Mxφ，Mφx。 图 2 和图 3 所示为壳中内力，图中所示方向皆为各力的正向。

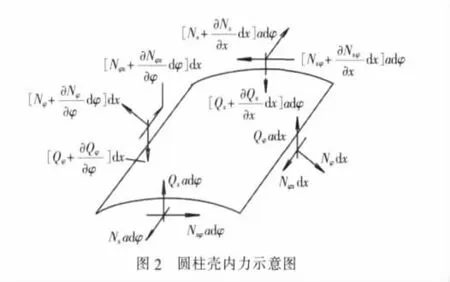
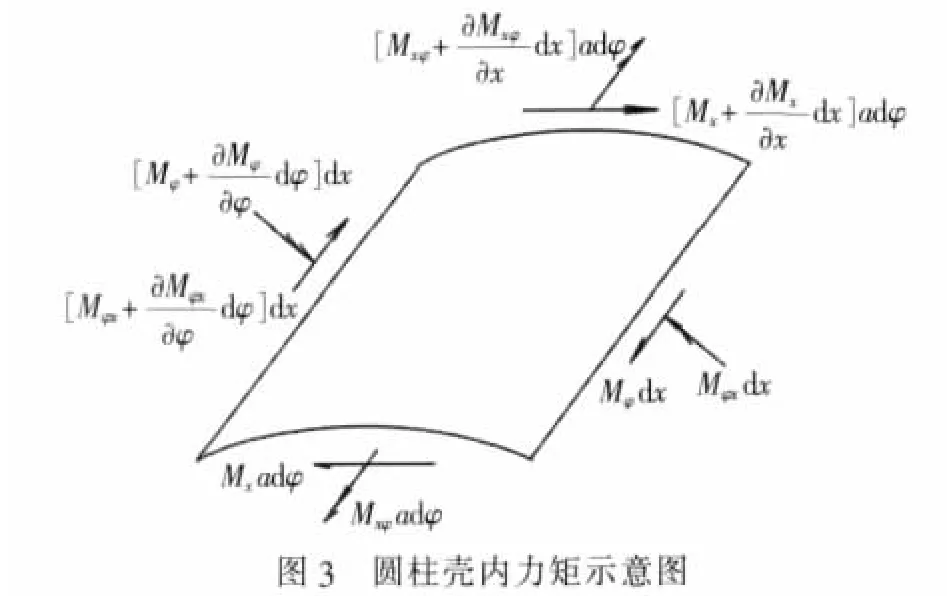
由内力与位移关系表达式［5］和内力平衡条件，得到以位移形式表示的的柱形薄壳静力微分方程式。

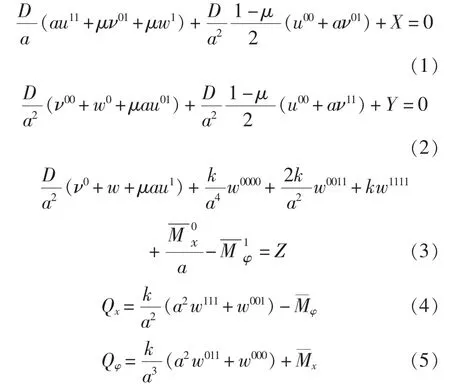
4 环肋圆柱壳的静力微分方程

环肋圆柱壳的纵剖面如图4所示，ξφ表示横向肋骨加强材的间距，dφ表示肋骨横截面的最大宽度，eφ表示肋骨横截面宽度、是高度z的函数。

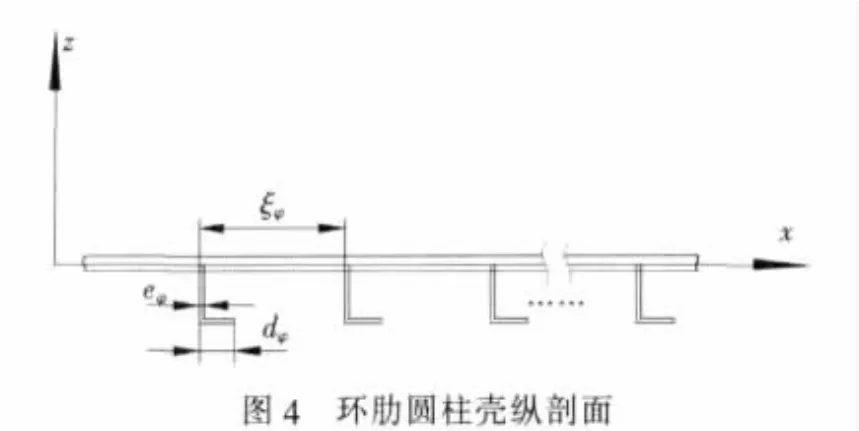
设横向肋骨加强材有nr个，则

函数f（x）如图5所示。假设加强材与壳体固结，即加强材与壳体内部变形规律相同，由此建立环肋圆柱壳的平衡微分方程式。

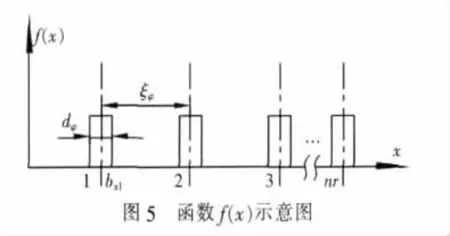
对于等间距密集分布的肋骨，当它们尺寸较小时，Huber建议肋骨的加强作用可以近似地认为均匀分布在两相邻肋骨之间的壳板上，这样引起的误差很小［8-9］。 所以

5 环肋圆柱壳静力微分方程的解

5.1 齐次微分方程的解

方程式（11）～式（13）对应的齐次方程组中，中面位移是x和φ的函数。因此，可以将位移设成傅里叶级数形式，进行变量分离，从而将偏微分方程化成常微分方程。

式中，A，B，C 为待定系数；λ＝nπ／l，l是壳长。u，ν，w 的形式已经满足了壳两端（x＝0，x＝l）简支的边界条件。

将式（11）～式（13）对应的齐次方程消元化简，然后分别得到u，v，w的8阶常微分方程，可以求得这3个微分方程的特征值相同，令其为mj（j＝1 ～8），并设积分常数 Anj＝αnjCnj，Bnj＝βnjCnj，将含有 αnj，βnj形式的解代回原方程就可以确定 αnj，βnj。所以，齐次方程的解为：

式中，Cnj（j＝1～8）是 8 个待定未知数，用于满足直边的8个边界条件。

5.2 微分方程的基本解

微分方程的齐次解是傅里叶级数形式表达的，因此外载也按傅里叶级数展开，即

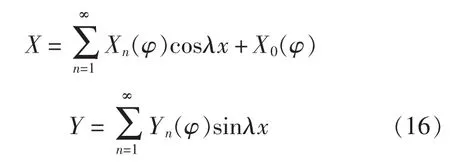
由于实际潜艇环肋圆柱壳上受到力矩作用工况较少，所以本文不讨论在外力矩作用下的基本解。外载F（x，φ）在x向被展开成了傅里叶级数形式，φ向的变化情况依外载沿φ向的分布不同而不同。先将外载分别取作沿x，φ，z向的3个单位点力，引进格林函数，求出单位载荷作用下壳体的位移，这就是基本解。然后就各种不同的外载对基本解沿φ向积分，积分的结果即为真实外力下的位移解。

壳体中面任意一点（x0，φ0）仅作用x向单位点力Fx为：

同样将式（24）、式（25）分别代入式（11）～式（13），按照上面x方向单位点力的求解过程求解，亦可以求出与式（19）～式（21）相类似的解。

5.3 微分方程的特解

对于在深水中的耐压潜艇圆柱壳的情况，圆柱壳在z方向受到均布压力p（负数）的作用，在x方向受到纵向压缩力T1的作用，作用在壳两端（x＝0，x＝l）壳中面上。 由平衡条件可以求得：

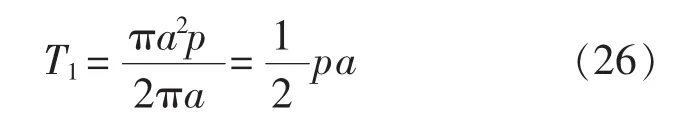
将X1，X2，Z分别展开成傅里叶级数后代入x向和z向仅作用单位点力的基本解中，沿φ向积分。求出X1，X2和Z作用下，壳体的位移为：

根据微分方程解的结构，通解加特解即为当前受力状态下圆柱壳的位移解。

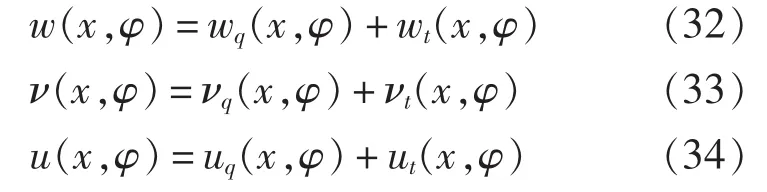
5.4 边界条件

由环肋圆柱壳的形状和受力状态可以确定边界条件为：

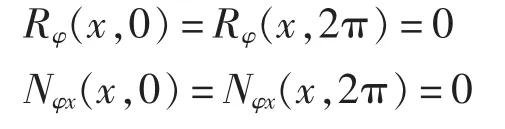
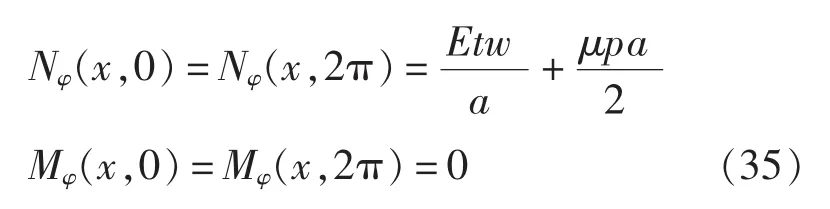
6 算例

下面对一个环肋圆柱壳的实例，分别应用本文的方法与传统的计算方法和有限元法计算其应力。环肋圆柱壳的计算参数如下：圆柱壳半径a＝1 m，圆柱壳长度 l＝4 m，壳板厚度 t＝16 mm，壳板弹性模量 E＝2.1×1011Pa，泊松比 μ＝0.3。 肋骨采用角钢 L80×50×6，间距 ξφ＝0.4 m，肋骨弹性模量和泊松比与壳板相同。圆柱壳受均布外压力，p＝－8×106Pa，两端简支。除此之外，为了模拟潜艇耐压壳在深水中的受力状态，环肋圆柱壳两端（x＝0，x＝l）还受到纵向压缩力作用，该力为一线分布力，单位长度上的大小为－pa／2＝4×106N／m。

将加强棱柱壳体法的计算理论编写成计算机程序，代入上面的计算参数计算，计算结果如表1所示 （计算结果只计算到傅里叶级数的前3项）。传统计算方法和有限元法的计算结果也一并列在表1中。

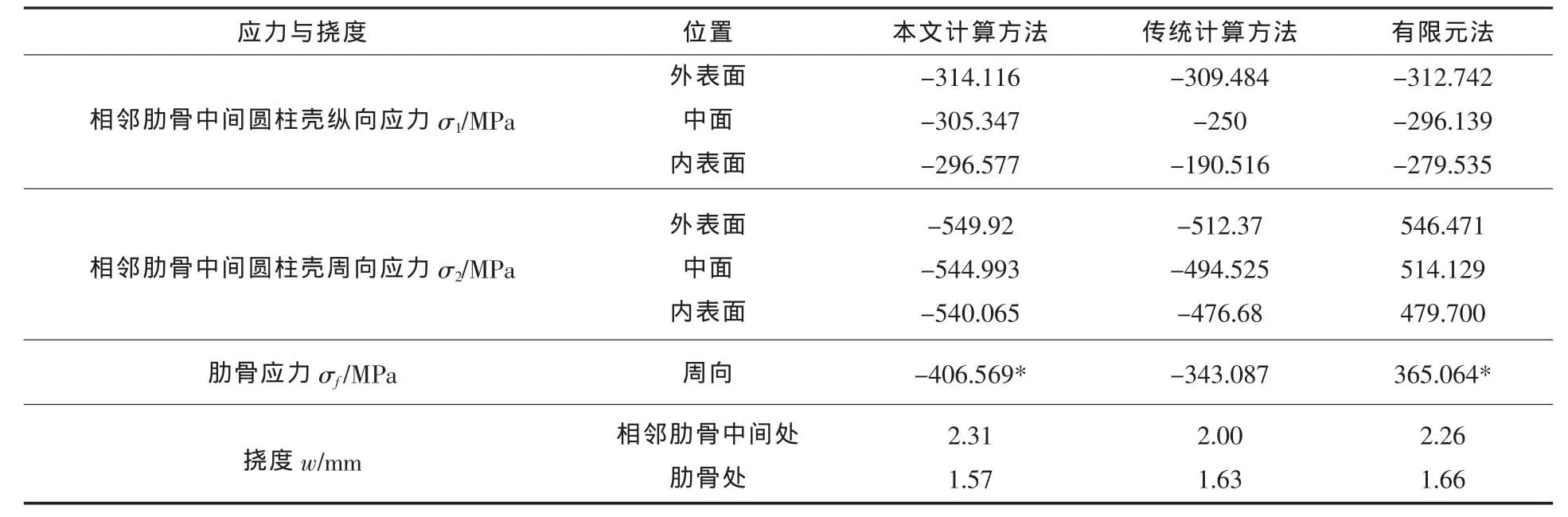
表1 环肋圆柱壳应力计算结果

7 结束语

加强棱柱壳体法在薄壳理论中引入阶跃函数，考虑了每一个加强材的具体位置和加强材的实际形状，建立起环肋圆柱壳的静力微分方程式，通过傅里叶级数，求出了微分方程的解析解。传统方法中没有考虑肋骨形状对壳体的影响，在计算结果中只能给出肋骨的平均应力，肋骨不同位置的应力则无法计算，加强棱柱壳体法则可以计算环肋圆柱壳任何位置的应力。

从表1可以看到，除环肋圆柱壳内表面纵向应力和肋骨周向应力外与传统计算方法计算结果相差较大外，其余应力和位移均与传统计算方法计算结果和有限元法计算结果相接近。对于内表面的纵向应力，本文方法的计算结果与有限元法结果相接近，但与传统方法计算结果相比，两者误差都较大；肋骨周向应力的有限元法结果与传统法结果较接近，本文计算方法误差较大，误差达18.5%。由外表面到内表面，环肋圆柱壳纵向应力和周向应力大小依次的递减规律也与传统的梁带理论观点相吻合。各应力的计算结果中，本文方法的计算结果普遍偏大，在最危险的位置，本文方法的计算结果比有限元法的结果仅相差0.06%，而比传统方法计算结果大7.2%。因此，在重要的结构中，计算环肋圆柱壳的应力时，建议用本文方法作辅助校核。

［1］许辑平.潜艇强度［M］.北京：国防工业出版社，1980.

［2］王晓天，许辑平.环肋圆柱壳应力计算中某些问题的研究［J］.应用科技，1990，8（1）：1－7.

［3］朱邦俊，万正权.环肋圆柱壳应力分析的一种新方法［J］.船舶力学，2004（4）：61－67.

［4］RIGO P.The Computation of prismatic structure applied to naval architecture ［J］.Marine Structure，1992，5（3）：313－332.

［5］RIGO P.Stiffened sheathings of orthotropic cylindrical shells［J］.Journal of Structural Engineering，1992，118（4）：926－943.

［6］NIE W，ZHOU S L，PENG H.SPSM and its application in cylindrical shells［J］.J Marine Sci Appl，2008（7）：40－47.

［7］徐芝纶.弹性力学（下册）［M］.北京：高等教育出版社，1995.

［8］FLUGGE W.Stress in the shells ［M］.Springer－Verlag Berlin，1960.

［9］MUKHOPADHYAY M.Stiffened plate in bending ［J］.Computer＆ Structure，1994，50（4）.

New Method for Stress Calculation of Ring－Stiffened Cylindrical Shell

Wang Xiao－ming1Chen Jie-gui2
1 China Ship Development and Design Center， Wuhan 430064， China
2 China Ship Research and Development Academy，Beijing 100192，China

Due to the limitation inherent to the traditional method， the stiffened prismatic shell method was incorporated into ring－stiffened cylindrical shell stress calculation.Using this method， a set of static force differential equations was established.Firstly，the ring－stiffened cylindrical shell displacement was dealt with the Fourier series and then the displacement solution was derived， further， the stress of ringstiffened cylindrical shell was obtained.Example calculations show that the stresses gotten by the new method are approximated to that by the traditional method and the Finite Element Method except the longitudinal stress inside the inner surface of ring－stiffened cylindrical shell and circumferential stress of ring， additionally， the longitudinal stress and the circumferential stress varying from outside to inside is the same as the traditional methods＇.

ring-stiffened cylindrical shell； stress calculation； stiffened prismatic shell method

U663.5

A

1673－3185（2010）05－49－05

10.3969/j.issn.1673-3185.2010.05.010

2009－10-09

王小明（1981－），男，硕士，助理工程师。研究方向：舰船结构设计与研究。E-mail：wangxiaoming2001＠126.com