弹塑性结构水下爆炸相似律研究

冯麟涵 刘世明 曹 宇 张阿漫

1海军装备研究院博士后科研工作站，北京 100161

2中国舰船研究设计中心，湖北 武汉 430064

3中国船舶及海洋工程设计研究院，上海 200011

4哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001

弹塑性结构水下爆炸相似律研究

冯麟涵1刘世明2曹 宇3张阿漫4

1海军装备研究院博士后科研工作站，北京 100161

2中国舰船研究设计中心，湖北 武汉 430064

3中国船舶及海洋工程设计研究院，上海 200011

4哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001

为实现将缩比模型在遭受水下爆炸冲击波载荷作用时的动响应特性结果推广到预测原型结构，根据相似理论，讨论了水下爆炸冲击波载荷相似率，并推导了弹塑性结构遭受水下爆炸冲击波载荷作用时的完全几何相似律。以典型舰船板架结构为研究对象，设计若干数值算例，结果表明缩比模型与原型结构之间的能量、运动响应和应力响应吻合较好，说明满足该相似率的缩比模型能够准确预测原型结构遭受水下爆炸冲击波载荷作用时的动响应特性，验证了该相似律的实用性。

弹塑性结构；相似理论；水下爆炸；动态响应

1 引言

如何准确预测水中结构物在受到水下爆炸冲击波载荷作用时的动态响应，一直是学术界普遍关心的问题［1-2］。最可靠的方法是实船试验，然而实船试验费用大，不易实施，目前国内外的研究者常使用缩比模型进行水池爆炸试验来模拟实船爆炸试验，以期获得接近于实际试验结果的有用信息［3－6］。故研究原型结构与模型结构之间各种力学和物理量的相似关系至关重要，只有完全了解原型结构与模型结构之间各种力学和物理量的相似关系，才能将水池爆炸的试验结果应用到实船的抗冲击性能及冲击环境的研究中。

本文根据量纲分析推导了弹塑性结构遭受水下爆炸冲击载荷作用时的完全几何相似律，讨论了相似理论在水下爆炸模型试验中的应用。并设计一系列数值试验，验证了满足该相似率的缩比模型能够准确预测原型结构遭受水下爆炸冲击波载荷作用时的动响应特性。

2 水下爆炸冲击波载荷相似理论

水下爆炸现象与一般水动力学现象不同［1］，它的作用力是冲击性的，水动力学中一些相似常数（如Re数等）不必考虑，一次冲击波不用考虑流体特性（如压缩性、重力等），对于水下爆炸冲击波，本文首先保证爆炸入射能量满足相似π定理。设药包质量为W（文中只考虑球形装药），爆距R，药包密度ρ，冲击波超压Pm，特征时间t，比冲量 I，流体密度 ρw，水中的声速 cw。

冲击波在流体域内固定的表面上所作的功可以表示为能流密度。能流密度是指冲击波在传播方向上经过某一固定面的单位面积内的能流，其表达式为：

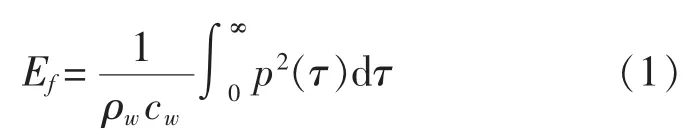
式中，ρw为水的密度，kg／m3； cw为水中声速，m／s。

由文献［2］可得：

在无限域流场中可认为冲击波能量均布于整个球形冲击波波阵面，则冲击波的入射能量为：

式中，E为冲击波总能量；Es为冲击波结构入射能量；Se为结构在垂直于冲击波波阵面上的投影面积。

将式（3）代入式（4）可得：

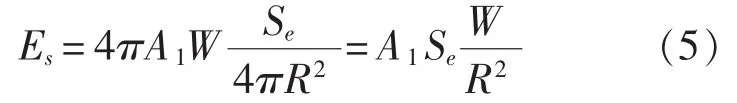
本文分析中一致使用相同的水介质和相同炸药密度，则 λρ＝1，λρw＝1。 水下爆炸冲击波载荷系统共有 8个变量［3］，分别为：冲击波入射能量 Es、结构在垂直于冲击波波阵面上的投影面积Se、爆距R、药包体积V、冲击波超压Pm、特征时间t、水中声速 cw、比冲量 I。取基本变量为 Es、R、t，其量纲矩阵如表1所示。

表1 水下爆炸冲击波外载荷系统的量纲矩阵

应用矩阵法导出无量纲π数如（6）式：

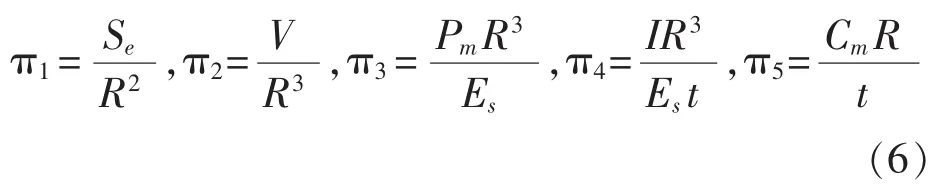
设爆距相似比为λR，且使用相同的水介质和相同炸药密度，即：λρ＝1，λρw＝1，λcw＝1。

按照上述相似准则模拟，模型的压力幅度与加载形式与原型相似，两者的压力幅度以及压力波的传播速度是相同的，而脉冲持续时间将按几何相似常数换算。

图1为通过经验公式计算得到的1 000 kg（TNT）炸药爆距为30 m处的冲击波载荷时历曲线图和1 kg（TNT）炸药爆距为3 m处的冲击波载荷压力时历曲线图。

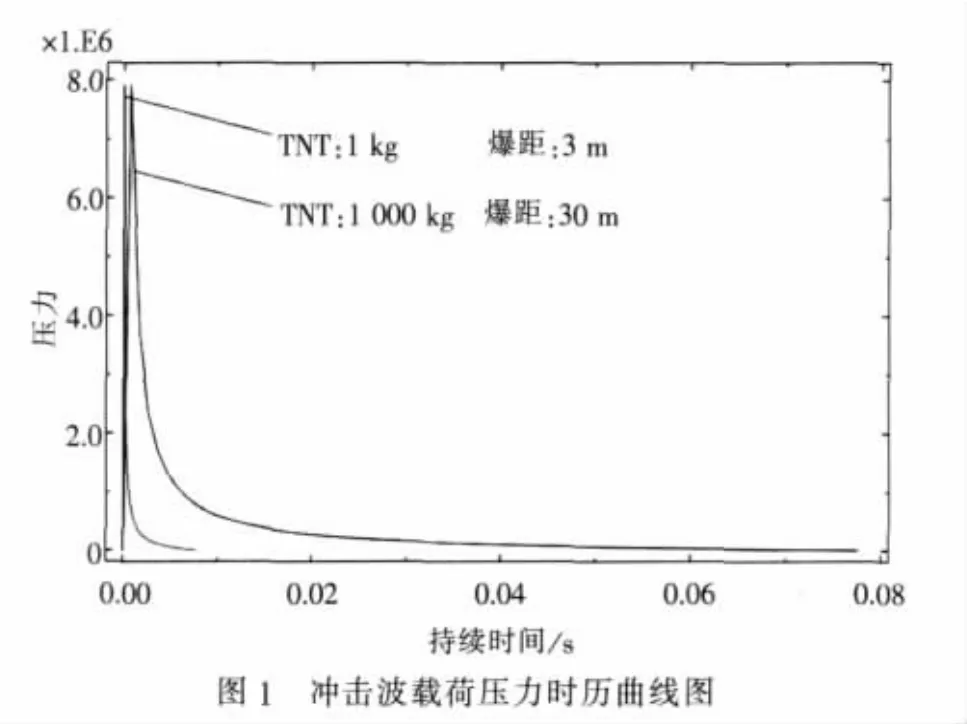
从图中可以看出，两者的压力幅度与加载形式相似，而脉冲持续时间按几何相似常数缩小，验证了本文通过相似理论推得的水下爆炸冲击波载荷相似理论是正确的，同时也证明了用经验公式计算得到的冲击波载荷是正确的。

3 弹塑性结构在冲击载荷下的响应相似律

对各向同性弹塑性材料而言，表征结构动态响应这一现象的物理量有：时间t、t时刻的位移w（t）、t时刻的应变 ε（t）、t时刻的应力 σ（t）、t时刻的应变率ε˙（t）、t时刻的外压力 P（t）、摩擦系数 f、泊松比 μ、弹性模量 E、屈服点 σs、质量密度 ρ、t时刻的结构尺寸 L（t）和切线模量 Et［7－8］。根据 π 定理对物理量的排列规定，上述13个物理量间的关系可写成一般函数形式：

以［L］、［F］、［T］作为基本量纲，则量纲矩阵如表2所示：

表2 水下爆炸冲击波外载荷下弹塑性结构响应系统的量纲矩阵

应用矩阵法导出无量纲π数如式（12）所示：

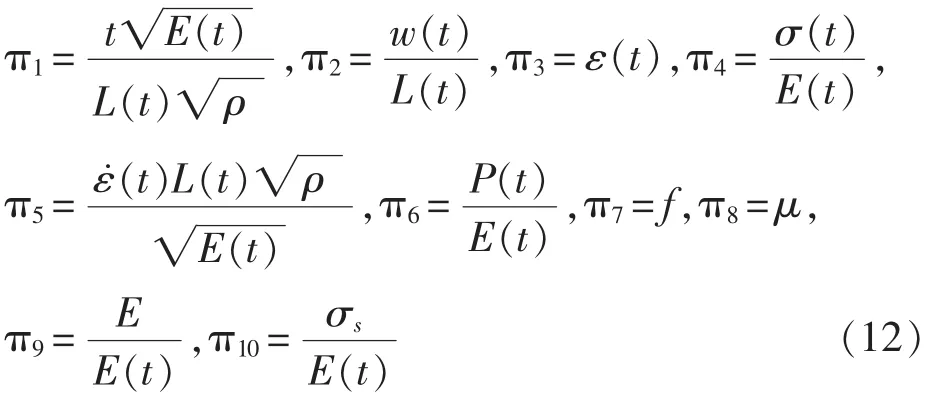
根据相似理论，要使模型与原型完全相似，各π项必须都相等，即

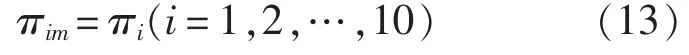
显然，当且仅当材料一致时，才能使π7、π8、π9、π10同时满足。 此时有

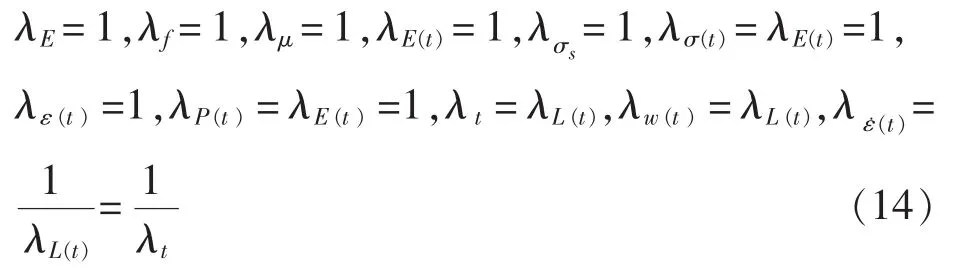
通常 λt取为常数（常为 λt＝ λL（0）），此时 t时刻速度相似倍数 λν（t）及加速度相似倍数 λa（t）为：

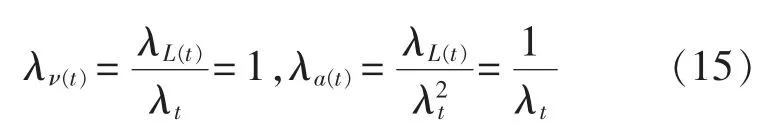
由上式可知，λν（t）及 λa（t）必为常数，从而 λL（t）也必为常数，因此，在动态响应分析中，只要时间相似倍数λt为常数，则在整个时间域内，相似系统的相似倍数均为常数，为便于计算，常取t＝0时间的几何尺寸倍数作为基本参数。

4 冲击载荷下弹塑性结构的相似性数值试验

板架结构是舰船和海洋工程结构物广泛采用的结构单元［9］，研究其水下爆炸动响应特性对提高舰船和海洋工程结构物的生命力有着极其重要的意义。然而由于水下爆炸问题的复杂性，对水中结构物在水下爆炸载荷作用下动响应问题开展精确理论研究十分困难。本文试图从板架结构着手研究水下爆炸结构物动响应的相似性问题。

4.1 数值计算模型

为了验证相似准则的有效性，设计一个板架结构，如图2所示。该板架由7根T型材作支撑，采用四边刚性固定的边界条件置于深水中，其有限元模型装配于流场后的模型如图3所示。此处分别取模型与原型几何相似比 λ ＝0.5、λ ＝0.2、λ＝0.1，结构原型与模型相似关系如表3所示。板架材料密度为 ρ＝7 800 kg／m3，弹性模量 E＝2.1e11 Pa，泊松比 μ＝ 0.3。

表3 板架结构原型与模型相似关系

4.2 数值试验结果分析

针对表3中所述工况，经计算得到原型和模型前10阶固有频率如表4所示。

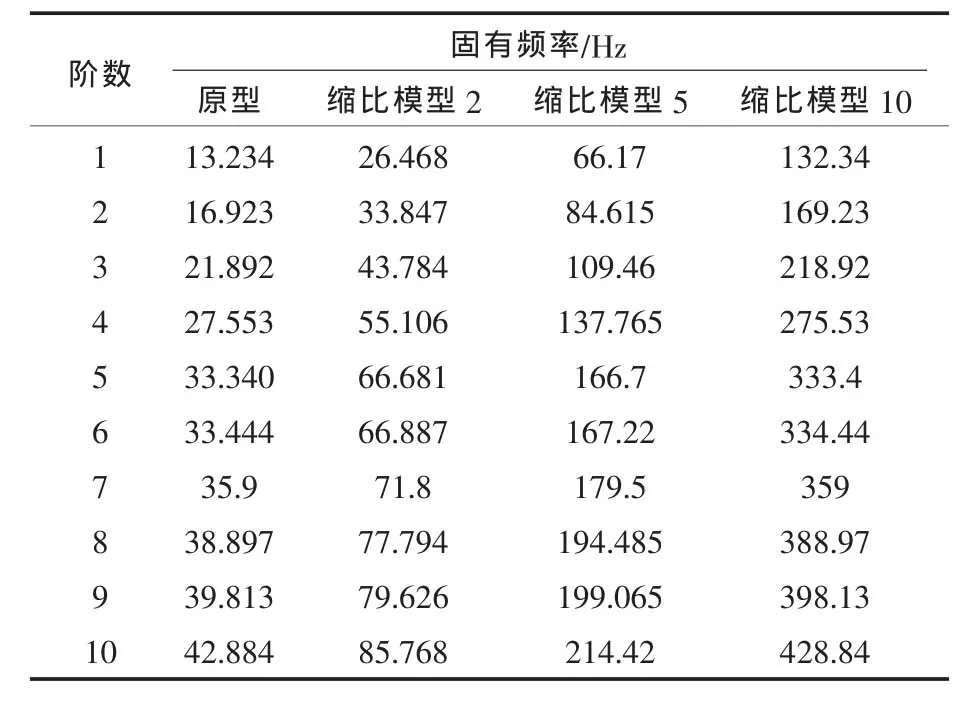
表4 原型和模型前10阶固有频率

按照缩尺比λf＝λL对各模型频率进行缩小，可以看出，原型和模型结构的各阶固有频率完全符合几何相似律。并且经计算得到各阶模态振型一致，也就是说，可以根据模型来准确预测原型板架结构的模态振型和固有频率。

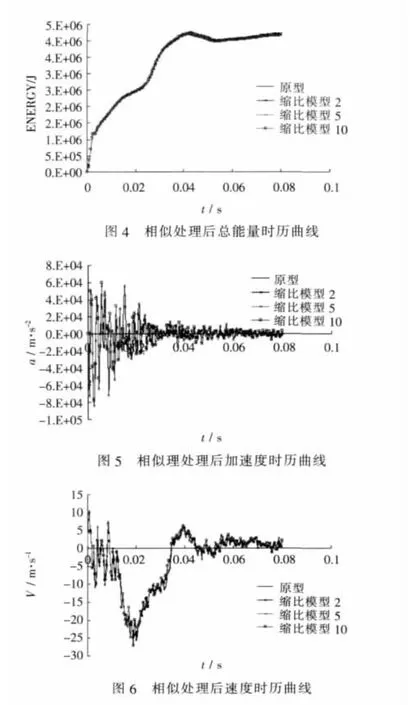
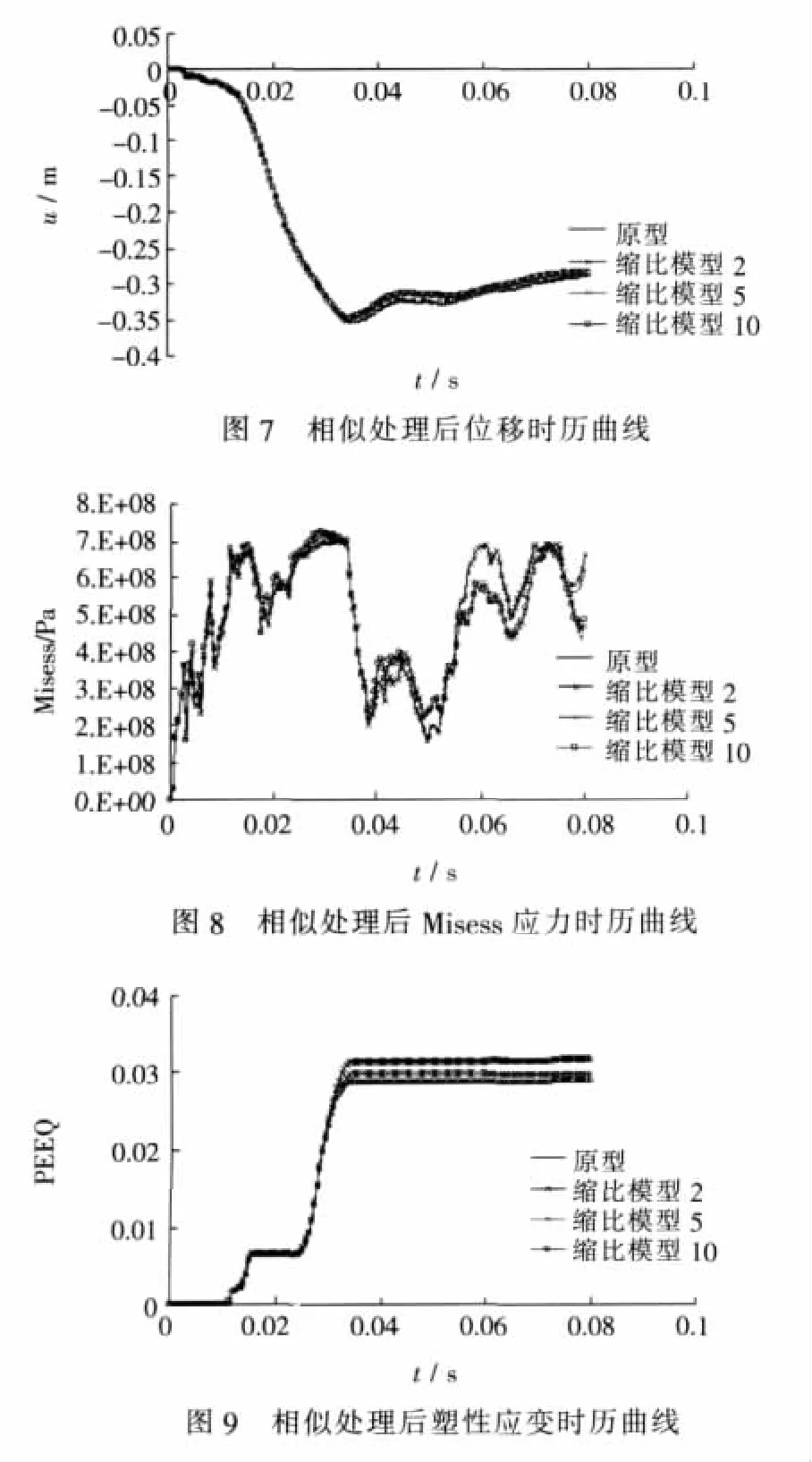
下面分别给出了进行相似变换后的板架结构遭受冲击载荷作用后的总能量时历曲线，并选取板架中心考核点的加速度、速度、位移、Misess应力、塑性应变时历曲线图。其中绘制各时历曲线点数相同，横坐标为t按λt放大，各纵坐标按相应缩尺比进行放大。

从图中可以看出，无论是在弹性还是塑性阶段，经过几何相似律处理后，原型和各模型的总能量、位移、速度、加速度、应力、应变时历曲线基本吻合，没有漏掉峰值的现象。从图8和图9可以看出，当缩尺比大于5时，模型的应变和应力将产生一定畸变，这可能是由于应变率效应［10］和其他未考虑因素的不相似所引起的。通过上述两图中可以看出其产生的畸变在工程允许范围内。故当选取同种材料、满足完全几何相似条件时，可以用模型来预测原型板架结构遭受水下爆炸时的动响应特性。

4.3 冲击因子相似性讨论

表3中的冲击因子在工程上的定义如式（19）所示：

目前较常用的冲击因子有两种形式：

式中，W为药包质量；R为爆矩；Se为结构在垂直于冲击波波阵面上的投影面积。

对于冲击因子目前学术界一直存在争议。作者认为冲击因子作为在长期工程实践中运用的一个评估参数，对于一定范围内的舰体目标损伤评估固然有其合理性和适用性，但是冲击因子中仅包含装药量和爆距两个物理量而不包括结构强度的因素。由于不包含目标特征参数，冲击因子必然有其片面性。作为更深入地研究舰艇结构在水下爆炸作用下损伤预报，需要利用相似理论对其进行深入的研究。

5 结 论

本文根据相似理论推导了弹塑性结构遭受水下爆炸冲击波载荷作用时的完全几何相似律，并且应用数值试验方法验证了相似律的正确性，通过完全几何相似模型能够准确预测原型结构遭受水下爆炸冲击波载荷作用时的动响应特性。所得主要结论如下：

1）提出水下爆炸冲击波载荷相似率，根据本文提出的相似条件能够保证水下爆炸冲击波入射相似，两者的压力幅度与加载形式相似，而脉冲持续时间按几何相似常数缩小。

2）提出弹塑性结构在水下爆炸冲击波载荷作用下动态响应的完全几何相似条件。

3）应用本文给出的相似率，能够简单有效的通过相似模型试验预测原型结构受水下爆炸冲击波载荷作用时的冲击响应特性。

4）冲击因子由于不包含目标特征参数，存在一定片面性，作为更深入地研究舰艇结构在水下爆炸作用下损伤预报，需要利用相似理论对其进行深入的研究。

［1］YOUNG S，Shin.Ship shock modeling and simulation for far－field underwater explosion ［J］.Computers ＆ Structures， 2005， 82： 2211－2219.

［2］HUNG C F.Elastic shock response of an air－backed plate to underwater explosion［J］.International Journal of Impact Engineering.2005，31：151－168.

［3］张孝慈.水下爆炸试验相似准则［J］.船舶力学，2007，11（1）：108－118.

［4］GELFAN B E，et al.Similarity criteria for underwater explosion ［J］.Combustion， Explosion， and Shock Waves，2004，40（2）：214－218.

［5］杨俊杰.相似理论与结构模型试验［M］.武汉：武汉理工大学出版社，2005.

［6］张维俊.船舶结构碰撞相似律的数值研究［J］.中国舰船研究，2009，11（3）：38－41.

［7］张振华，陈平毅，漆万鹏，等.舰船局部板架结构在水下爆炸冲击波下动态响应的相似律研究［J］.振动与冲击，2008，27（6）：81－86.

［8］谢建林.瞬态载荷作用下弹塑性结果动响应相似性研究［D］.哈尔滨：哈尔滨工程大学，2008.

［9］ANDRIC J，ZANIC V.The global structural response model for multi－deck ships in concept design phase［J］.Ocean Engineering， 2010，37（8/9）：688－704.

［10］姚熊亮.舰船结构振动冲击与噪声［M］.北京：国防工业出版社，2007.

Investigation on the Similarity Criterion of Elastic-Plastic Structures Subjected to Underwater Explosion

Feng Lin－han1 Liu Shi－ming2 Cao Yu3 Zhang A－man4
1 Postdoctoral Research Center， Naval Academy of Armament， Beijing 100161， China
2 China Ship Development and Design Center， Wuhan 430064， China
3 Marine Design and Research Institute of China， Shanghai 200011，China
4 College of Shipbuilding Engineering， Harbin Engineering University， Harbin 150001， China

Extending the dynamic response characteristics of scale model under shock wave loading of underwater explosion to the prototype structure prediction，the similarity rate of underwater explosion shock wave loading was examined based on the similarity theory，and then the fully geometric similarity criterion of elastic－plastic structures was obtained.Taking the typical ship gross panel structure as the research object， numerical calculations were carried out.The results show that the energy， motion and stress responses of the scale model agree well with those of the prototype structures，indicating that the scale model meeting the similarity rate can accurately predict the dynamic response characteristics of the prototype structures subjected to underwater explosion，and thus demonstrating the practicability of the similarity criterion.

elastic-plastic structure； similarity theory； underwater explosion； dynamic response

U661.43

A

1673－3185（2010）05－01－05

10.3969/j.issn.1673-3185.2010.05.001

2009－10-12

中国博士后科学基金特别资助项目（200801104）；高等学校博士学科点专项科研基金（20070217074）

冯麟涵（1981－），女，博士。研究方向：舰船抗冲击性能评估。E-mail：fenglinhan1225＠yahoo.com.cn