基于传递矩阵法的船舶轴系回旋振动计算研究
刘 刚 吴 炜 饶春晓 陈汝刚
中国舰船研究设计中心,湖北 武汉 430064
基于传递矩阵法的船舶轴系回旋振动计算研究
刘 刚 吴 炜 饶春晓 陈汝刚
中国舰船研究设计中心,湖北 武汉 430064
分析船舶轴系回旋振动的传递矩阵计算方法,建立集总参数元件-分布参数元件混合系统模型,得出各种简化模型的传递矩阵。以某型海事巡逻艇为例,对传递矩阵计算方法中影响计算结果的主要参数进行分析,提出参数的选取方法,为回旋振动特性分析提供依据。
轴系;回旋振动;传递矩阵;模型
船舶在运行中,由于旋转质量 (主要是螺旋桨)的不平衡力离心力、螺旋桨上的流体激振力以及螺旋桨偏心质量的重力作用,会使轴系产生回旋振动[1-3]。国外一些主要船级社和国内的“钢质海船入级与建造规范”等都对轴系的回旋振动提出了相应的技术要求。
目前,轴系回旋振动频率的精确计算主要采用传递矩阵法[4,5],但是,由于计算模型中一些参数可能的不确定性,计算结果可能存在较大的误差。本文以某海事巡逻艇为例子建立集总—分布混合模型,利用传递矩阵法计算轴系回旋振动固有频率,并分析了所建模型中主要参数的选取对计算结果的影响,为轴系设计中回旋振动特性分析提供依据。
1 回旋振动当量模型
按照 “船舶推进轴系回旋振动计算方法”(CB*/Z 336-84)中的规定,轴系回旋振动当量模型的度量方法,是从螺旋桨端开始,到柴油机飞轮或传动齿轮箱中的大齿轮首端或弹性联轴节的从动部分为终止点。
采用集总参数元件—分布参数元件混合系统,将研究对象的轴系简化为三类元件:螺旋桨简化为匀质刚性圆盘元件;中间轴、艉轴和螺旋桨轴简化为匀质轴段元件;各轴承简化为支承元件。建立的振动当量模型如图1所示。
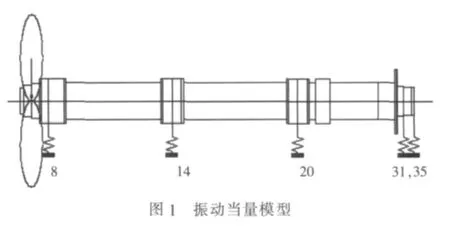
其中,8号为艉轴架轴承,14号为艉轴管轴承,20号是中间轴承,31号、35号为齿轮箱支承轴承。
2 回旋振动的传递矩阵法
通过当量模型的建立,将轴系由复杂的弹性系统分解为一系列惯性元件和弹性元件连接而成的简单模型。按照一般结构静力学的线性理论,任两个相邻端面的状态矢量通过一个线性变换联系着,也就是相邻两端面的状态矢量用一个矩阵相互联系着,变换矩阵把状态矢量从此端面迁移或传递至彼端面。
传递矩阵法[6]就是将这些元件的结合面作为计算端面,列出元件端面处的状态矢量,然后,利用弹性系统各部分之间的传递关系,列出传递矩阵,最后,将各个元件逐个地连接起来,连续相乘得到系统的传递矩阵并求解。
2.1 状态矢量定义
系统各元件端点的状态矢量是该元件状态参数所构成的列阵。对于当量模型,元件端面的状态由其挠度、转角、弯矩、剪力组成。任意截面的状态由矢量表示如下:

式中,Zi为端面的状态矢量;i为元件序号;m为端面上标,m=L(左端),m=R(右端)。
2.2 各类元件传递矩阵
1)匀质圆盘元件
模型中将螺旋桨简化为刚性匀质圆盘元件,元件质量m,极转动惯量Jp,径向转动惯量Jd,元件的质量和转动惯量均应考虑附连水效应。计算固有频率时,可不计阻尼作用,元件传递矩阵如下:

式中,Ω为振动频率;h为频率比,轴转速与振动频率之比。
2)匀质轴段元件
回旋振动模型将各轴段按自然分段为等截面的匀质轴段元件。传递矩阵考虑轴段受到的弯矩,剪力影响,以及惯性力和惯性力矩的作用。传递矩阵如下所示:

式中参数详见文献[6]。
3)支承元件
模型中,假定支承元件刚度各向相同。混合模型中,由于轴段作为匀质轴段元件处理,这时支承元件是一无质量、无弹性的伪元件。其传递矩阵:

式中,Ke为支承元件的等效刚度。
2.3 固有频率的计算
各元件状态矩阵连续相乘即得到轴系集总-分布参数等效系统的累积矩阵。考虑到当量系统始端元件螺旋桨的左端边界总是自由的,其状态矢量中的力与弯矩分量恒为零,得到轴系始末端状态矢量有以下关系:

根据系统末端边界条件,得到在不同频率比下(即轴转速与固有频率之比),轴系的固有频率。
系统末端为刚性铰支时,其边界条件为:

系统末端为自由端时,其边界条件为:

系统末端为固定端时,其边界条件为:

3 模型参数影响分析
3.1 轴承支承刚度
轴承支承系统刚度由三部分组成,如图2所示:油膜(水膜)刚度K1,轴承—轴承座刚度K2和船体基座刚度K3。由于刚度计算相当复杂,而且影响因素很多,回旋振动计算中,一般用一等效刚度K作为轴承刚度。
国内外有关机构和标准给出了轴承等效刚度的选取范围,如表1所示。
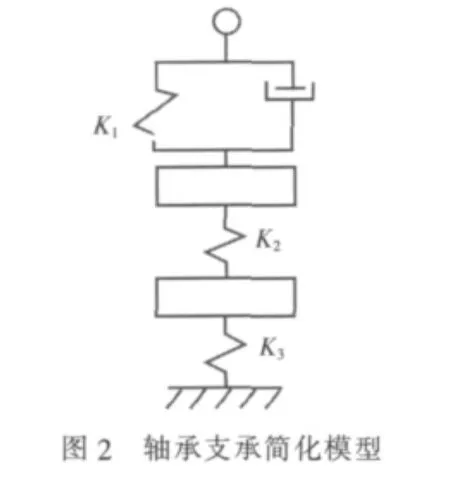
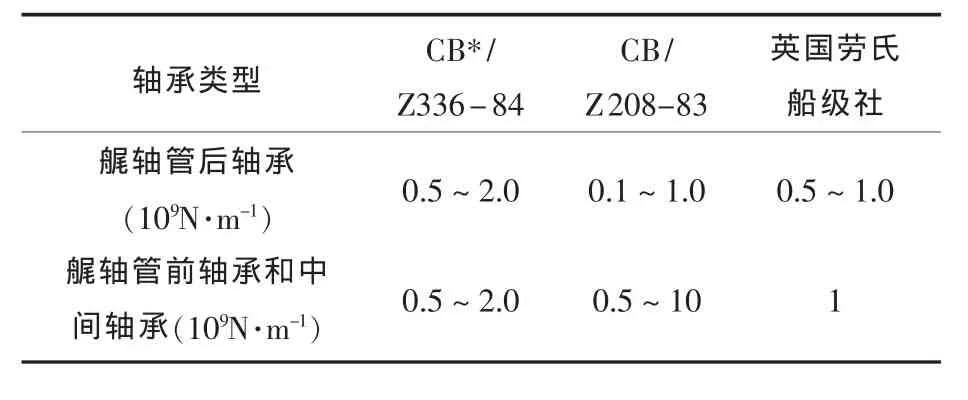
表1 轴承等效刚度
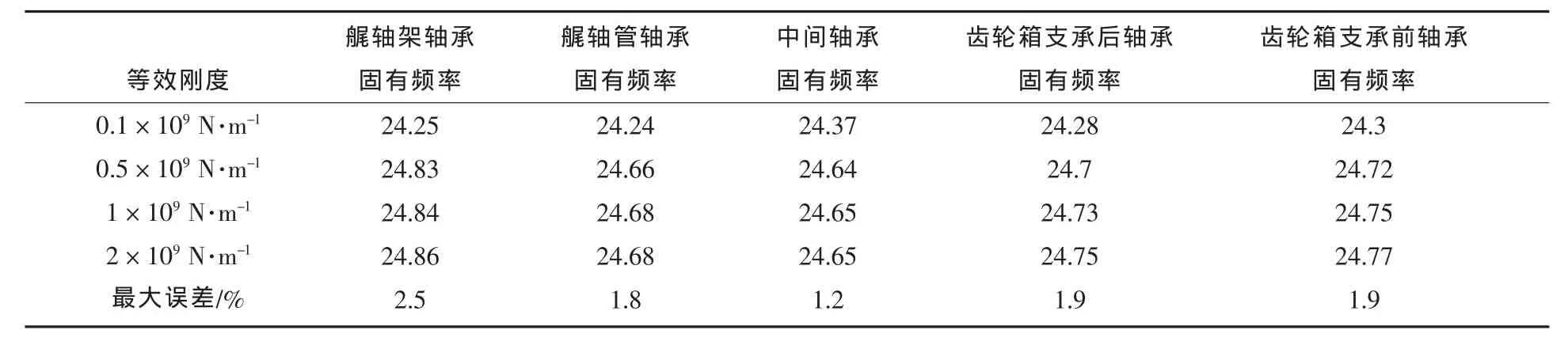
表2 轴承等效刚度对回旋振动固有频率影响
结果表明:
1)艉轴架轴承刚度变化对回旋振动固有频率影响最大。
2)对于该型船的轴系,轴承等效刚度在0.1×109~2×109N·m-1范围内时,轴系回旋振动固有频率变化不大,在工程允许范围以内。
3)越是靠近船艏的轴承,刚度变化对固有频率影响越小。但齿轮箱轴承例外,这是因为齿轮箱轴承附近有大齿轮,增大了对固有频率的影响。
3.2 轴承支承点
回旋振动计算分析中,一般将轴承简化为单点支承。对于中间轴承、艉轴管轴承等,支承反力可以认为是分布均匀的,支承点近似假定在轴承中央位置。但对于艉轴架轴承,由于受悬臂端螺旋桨的作用,轴承支反力沿轴承长度分布很不均匀,支承点偏向船尾。螺旋桨越重,桨轴弯曲刚度越小,支承点偏离轴承中央位置就越多。有关机构给出了艉轴承支承点选取的近似选取范围,如表3所示。
对于水润滑轴承,支承点的选取一般参考铁梨木轴承。在支点位置取距轴承衬后端1/4~1/3L长度范围时,计算得到的回旋振动固有频率如图3所示。
结果表明,艉轴架轴承支点位置对计算频率影响较大,相差达8%,因此必须合理选取。10支承模型,通过轴系动态较中计算,求出各支承点处的轴承支反力,进而求出轴承单点支承的等效位置[7-9]。
汽轮机组的低压缸排汽被循环水冷却成凝结水时,体积大幅度缩小,凝汽器内部形成高度真空,所有与之相连的设备或系统若不严密,都会向凝汽器内漏入空气,因低压缸排汽中的不溶于水的气体,将会使凝汽器内的压力逐步升高、真空度下降。如果这些与凝汽器相连的设备或系统的真空严密性较差,可能会有以下几点危害:
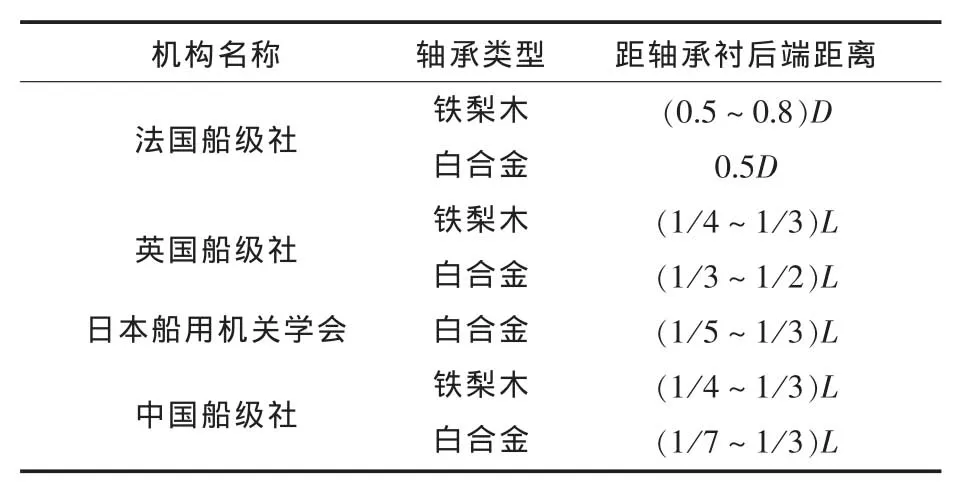
表3 艉轴架轴承支承点位置

支承点距轴承衬后端距离为:
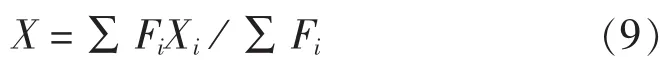
式中,X为等效单支承距轴承衬后端距离;Fi为第i个支点支反力;X为第i个支点距轴承衬后端距离。
根据上述计算,得出艉轴架轴承支点位置距轴承衬后端 0.29 L,在规范规定的(1/4~1/3)L 之间。
3.3 螺旋桨附连水效应
螺旋桨在水中运转振动时,有一部分振动能量传递给水。在振动计算时,将这部分能量用参与振动的附连水质量及转动惯量计入,并把它加到螺旋桨的质量和转动惯量上。
考虑附连水效应时,通常是直接给螺旋桨质量和转动惯量乘以给定的附连水系数。根据“船舶推进轴系回旋振动计算方法”(CB*/Z336-84)规定,质量附连水系数一般取 1.1 ~ 1.3,极转动惯量附连水系数取 1.25~1.3,径向转动惯量附连水系数取 1.5 ~ 1.6。
但是,采用固定的附连水系数没有考虑到螺旋桨几何尺寸、运动方向、海水密度等影响,计算结果往往误差较大。
本文采用Schwanecke H提出的二维振动翼理论求得的附连水质量Δm、附连水极转动惯量ΔJp和附连水径向转动惯量ΔJd。该方法将螺旋桨叶片的展开近似看为椭圆,具有一定的精度,而且公式简单,具有工程应用价值。

式中,ρ为海水密度,kg/m3;Dp为螺旋桨直径,m;Zp为螺旋桨叶片数;为螺旋桨平均螺距比;为螺旋桨盘面比。
根据上述方法,得出该型船螺旋桨质量附连水系数为 1.33,极转动惯量附连水为 1.5,径向转动惯量附连水系数为2.1。得出的附连水系数均高于规范一般选取的上限值,因此在轴系设计过程中,作回旋振特性分析时,采用二维振动翼理论计算附连水系数,更能保证轴系设计的安全性。
4 结论
在船舶轴系设计中,必须进行回旋振动特性分析,使设计轴系的回旋振动特性满足相关规范的要求。而回旋振动计算中,模型参数的合理选取是主要难点,一方面要保证计算结果的准确性,另一方面要保证轴系设计的安全性。
本文针对某海事巡逻船,利用传递矩阵法计算轴系回旋振动频率,通过分析模型中主要参数对计算结果的影响,提出以下参数选取方法:
1)艉轴架轴承刚度变化对回旋振动固有频率影响较大,刚度应取规范中的下限。其它轴承对计算结果影响较小,而且刚度较大,取0.5×109N·m-1以上均可。
2)艉轴架轴承支承点的选取,对计算结果影响很大,可通过合理校中计算得出,以保证计算精度。
3)螺旋桨附连水系数采用二维振动翼理论求得,相比于传统的取固定系数方法,具有一定的准确性,而且轴系设计更加安全。
[1]谭祖盛,陈川艾,郭贤民.高速船推进轴系回旋振动影响因素及特点探析[J].船舶工程,1999(3):32-34.
[2]梁向东.轴系的回旋运动对船舶噪声的影响[J].噪声与振动控制,2007,27(2):69-70.
[3]何灵聪,黄次浩,朱从乔,等.轴系回旋振动的计算机测试系统研究[J].海军工程学院学报,1997(3).
[4]陈锡恩,高景.船舶轴系回旋振动计算及其参数研究[J].船海工程,2001(5):8-11.
[5]周瑞平.基于VB的船舶轴系回旋振动计算软件[J].造船技术,1999(3):30-33.
[6]陈之炎.船舶推进轴系振动[M].上海:上海交通大学出版社,1987.
[7]耿厚才,王万华.巨型油轮轴系校中模型分析[J].船舶工程,2007,29(1):17-19.
[8]魏海军,王宏志.船舶轴系校中多支承问题的研究[J].船舶力学,2001,5(1):49-54.
[9]周瑞平,张升平,杨建国.三弯矩方程的改进及在船舶轴系动态校中中的应用[J].船舶工程,2003,25(1):40-43.
Numerical Calculation of Whirling Vibration of Ship Shafts Based on Transfer Matrices Method
Liu Gang Wu WeiRao Chun-xiao Chen Ru-gang
China Ship Development and Design Center,Wuhan 430064,China
The method of transfer matrices used for whirling vibration of ship's shafts was analyzed, then various simplified models of transfer matrices were obtained by building a hybrid model for lumped parameter elements and distributed parameter elements.Verified by an example of a maritime patrol vessel,the method of parameter selection was proposed by analyzing the main parameters influencing the calculation results in transfer matrices method,which could provide evidence for the analysis of the characteristics of whirling vibration.
shaft system;whirling vibration;transfer matrices;model
U664.8
A
1673-3185(2010)01-60-04
2009-03-12
刘 刚(1982-),男,助理工程师,硕士研究生。研究方向:船舶推进系统设计。E-mail:toeet@sina.com

