用尺规作正多边形
钱国栋
(河北北方学院信息与工程学院,河北 张家口 075000)
在平面上用直尺 (无刻度)和圆规作出的图是有限的.这里只讨论常见的正多边形的尺规作图,这种作图也可归结为圆内接正n边形的作图.为此,先用圆规把单位圆分成n等分,连结其分点就得一个正 n边形,或者求出单位圆内接正n边形的一条边长,再在单位圆上截取,作出一个正n边形.由所得的正 n边形和多边形相似定理,就可作出所要求的正n边形.
用圆规及直尺作图的过程,是要经过以下的步骤:
①在已知范围内挑选一点.②过两点可以作一直线.③已知圆心和半径可以作一圆.④假如两直线(圆)或一直线一圆能够作出,如果有交点,那么它们的交点能够作出.
一个初等几何图形能够作出,只不过有限次的重复.引用上面四种步骤或其部分,作出一些所要求的点、直线和圆.为了讨论所要求的图形是否可作的问题,可在解析几何中叙述上述作图过程.一点能够任意排选,可以假定它的坐标是有理数;过坐标是有理数域Q中数的两点的直线,它的方程的系数也是Q中的数;因为系数在Q中两个二元一次方程组有解时,它的解仍在Q中,因此所给两条直线有交点时,其交点的坐标也在Q中;如果圆上的三个点,或一个点及圆心,它们的坐标都在Q中,那么圆的方程的系数也在Q中,但方程的系数在Q中的两圆或一圆及一直线的交点的坐标一般含有Q中数的平方根.因此,一个数 x是方程的系数在Q中两直线、两圆及一直线和圆的交点坐标,那么 x能够用Q中数的有理运算及平方根表示,反之亦成立.
我们把有理数域Q换成数域下,上述的推导亦成立.
定理1 数 x能够用尺规作出,当且仅当它能够用 F中数的有理运算及平方根表示.
通常能作的正多边形,都由定理1给出,设已知圆的半径R=1,又因为
下面讨论正17边形的作法
假设单位圆的圆周分成十七等分,其分点是 A,Ai,i=0,1,2,…,16,并且 AA0是圆的直径,记AA0=a0,AAi=ai,那么 a0=2,al=a17-l(1≤l≤16)见下图,在 [1]中,能算出 (a8可以由以下算出).

和

具体作法见文献 [1].
当an可由尺规作出时,那么也可由尺规作出.
考虑到等分一个角是可行的,就可作出边数是3×2k,4×2k,5×2k和17×2k的正多边形.[2,3]
熟知,作正n边形与把单位圆n等分是一会事,我们把单位圆6等份,再10等份,它们每一等份所对应的圆心角的差:60°-36°=24°,而360°÷24°=15,所以在作出正 6边形和正 10边形后,就可以作出正15边形,从而也能作出正15×2k边形.因为正17边形能作出,即把圆周能17等分,其一等分所对应的圆心角是,把它2等分,所对应的圆心角是,再把圆10等份所对应的圆心角是36°,而,并且=85,所以正85边形可以作出;从而也能作出正85×2k边形;因为正24边形能作出,把圆围能24等分,其一等分所对应的圆心角是15°,又因为正136边形能作出,所以可以把圆周能136等分,每一等分所对应的圆心角是,取这角的3倍,所得的圆心角是,所以取 15°圆心角与圆心角的差:15°并且有因此正51边形可以作出,从而可作出51×2k边形,于是可得.
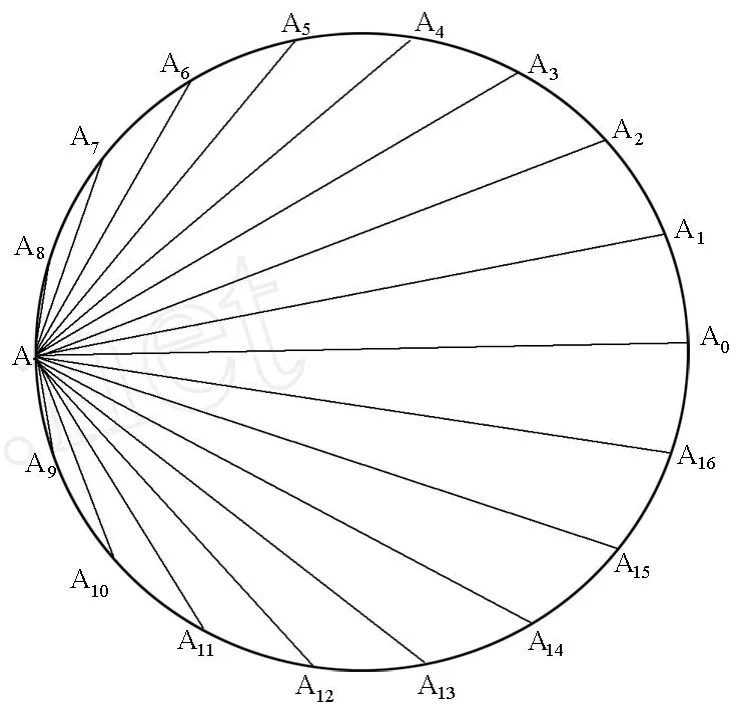
图1 系统的状态响应曲线
定理2 用尺规能作出边数不超过100的正多边形,如下表所示.
边数不超过100的正多边形,我们作出上表中的24个,其余74个均不能作图,这可由如下的高斯定理予以解答 (见 [1]).
定理3 仅用尺规把圆周 n等分,当且仅当 n是如下形状的整数.
(1) n=2m;
(2)n=P=22t+1,且 P是素数;
(3) n=2mP1P2…Pl,Pi(i=1,2, …,l)是22t+1型的素数且各不相同.
不能用尺规作出的正多边形,也可由文献 [4]、[5]从理论上阐述,这里不再多叙.
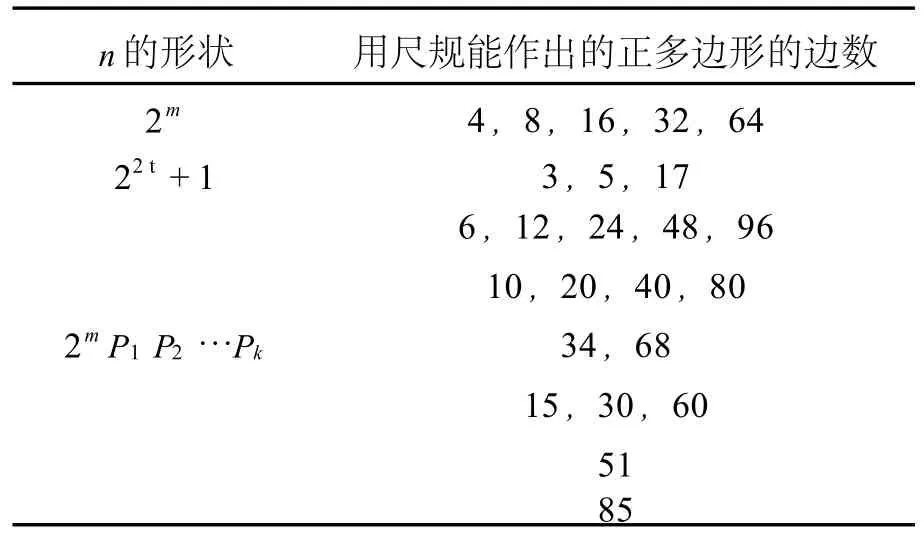
表1 用尺规作出正多边形的边数
[1] 梁绍鸿.初等数学复习与研究 [M].北京:人民教育出版社,1958:9-70
[2] 马忠林,张贵新.中学几何教学论 [M].沈阳:东北师大出版社,1988:20-80
[3] 陈通鑫,何怡生.世界几何名题趣谈 [M].石家庄:河北教育出版社,1989:15-46
[4] 霍元极,寇福来.高等代数 [M].北京:北京师范大学出版社,2009:1-10
[5] 熊全淹.近世代数 [M].武汉:武汉大学出版社 (第二版),2004:5-36

