积和式的拉普拉斯展开式探析
赵宪民
(莱芜职业技术学院,山东莱芜271100)
1 记号及基本性质
积和式由著名数学家Binet和Cauchy引入.数学家Muir创造了术语“permanent”来示定义在 n阶矩阵A=(aij)的下列函数:

其中,sn表示n次对称群,(1)式中右方称为积和式的展开式.从此,积和式的研究蓬勃发展[1],研究更加活跃,获得了许多成果[2-4].同时,积和式在纯粹数学、应用数学、物理学,特别是组合设计中都有广泛的应用,更加体现了它的重要性.
从 (1)式看,积和式的表示式与n阶矩阵A=(aij)的行列式anσn.式中每一项相差一个符号因子(-1)τ(σ1…σn).这就给出提示,可以用类比方法得到积和式的一些相关事实.先列出一些基本的事实.
定义1[1]在一个n级行列式D中任意选定k行k列(k≤n).位于这些行和列的交点上的 k2个元素按照原来的位置组成一个 k级行列式M,称为行列式D的一个k级子式.在 D中划去这k行k列后余下的元素按照原来的位置组成的n-k级行列式M′称为k级子式M的余子式.
定义2[1]设D的k级子式M在D中所在的行、列指标分别是 i1,i2,…,ik,j1,j2,…,jk.则M的余子式M′前面加上符号 (-1)(i1+i2+…+ik)+(j1+j2+…+jk)后称做 M的代数余子式.
定理1[1](拉普拉斯定理)
设在行列式D中任意取定了k(1≤k≤n-1)个行,有这 k行元素所组成的一切k级子式与它们的代数余子式的乘积的和等于D.
性质1 设 A′表示A的转量矩阵,则per A′=per A.即
性质1说明积和式对列成立的性质,对行也成立.下面,对列的形式进行叙述.
记矩阵 A=(a1,a2,…an),其中 a=(a1j,a2j,…anj)′,j=1,2,…,n.则per A=per(a1,a2,…an).
性质2[2]per(a1,…,ai,…aj,…,an) =per(a1,…,aj, …ai,…,an).
性质3[2]per(a1, …,αi+βi, …aj, …,an) =per(a1, …,αi, …aj, …,an) +per(a1, …,βi,…aj, …,an).
2 积和式的Lap lace展开式
为了证明积和式的拉普拉斯展开式,先引入一个概念.
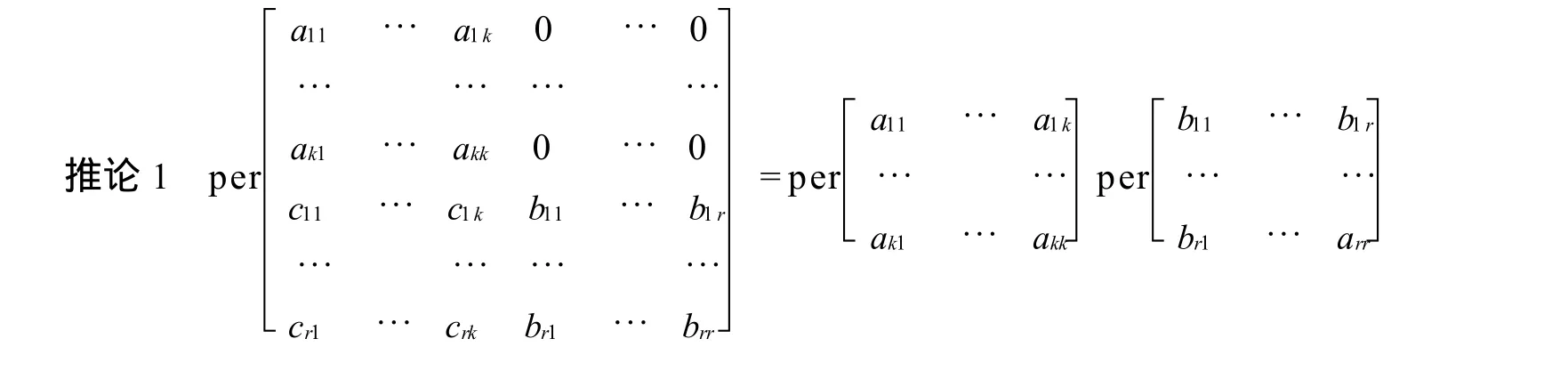
定义3 在一个 n阶积和式per A中任意选定第i1,i2,…,ik行和第j1,j2,…,jk列 (k≤n),位于这些行和列的交叉处的k2个元素按原来的次序组成一个 k阶积和式记为per A [i1,i2,…,ik|j1,j2,…,jk]称为积和式per A的一个k阶子积和式;在per A中划去这样的k行k列后余下的元素按照原来的次序组成的n-k阶积和式称为k阶积和式per A [i1,i2,…ik|j1,j2,…,jk]的余子积和式,记为per A [i1,i2,…in-k|j1,j2,…,jn-k].
引理1 n阶积和式per A中的一个k阶子积和式per A [i1,i2,…ik|j1,j2,…jk]与它的n-k阶余子积和式per A [i1,i2,…in-k|j1,j2,…jn-k]的乘机中的每一项都是积和式per A展开式中的一项.
证明 首先讨论k阶子积和式位于per A的左上方,即i1=1,i2=2,…,ik=k,j1=1,j2=2,…,jk=k的情形.


因此per A [1,2,…k|1,2,…,k] ·per A [i1,i2, …in-k|j1,j2, …,jn-k]中每一项都是per A中的一项.
再证明一般情形.
设i1<i2<…<ik;j1<j2<…<jn.采用下面交换行、列的次序的方法将per A [i1,i2,…ik|j1,j2,…,jk]变到位于per A的左上角.为此,先把第i1行依次与第i1-1,i1-2,…,2,1行做对换.这样经过了i1-1次对换而将第i1行换到第一行.再将i2行依次与第 i1-1,i1-2,…,2行对换而换到第二行,一共进行了i1-2对换.如此进行下去.一共进行了
(i1-1) + (i2-2) +…+(ik-k) = (i1+i2+…+ik) -(1+2+…+k)次行变换而把第i1,i2,…,ik行依次换到第1,2,…,k行.
利用类似的列变换,可以将 j1,j2,…,jk列换到1,2,…,k.一共作了
(j1-1) +(j2-2) +…+(jk-k) =(j1+j2+…+jk) -(1+2+…+k)次列变换.
记变换后得到的积和式为per B,则由性质2有per A=per B.
现在per A [i1,i2,…ik|j1,j2,…,jk]位于per B的左上角,此时per A [i1,i2,…in-k|j1,j2,…,jn-k]一定位于per B的右下角,所以per A [1,2,…k|1,2…,k] ·per A [i1,i2,…in-k|j1,j2,…,jn-k]中的每一项都是per B即per A中的每一项,这就是所要证明的结论.
有了以上的准备工作,下面给出积和式的Lap lace展开式.
定理2 设在积和式per A中任意取定k(1≤k≤n-1)行,由这 k行元素所组成的一切k阶子积和式与它们的余子积和式的乘积之和等于积和式per A.
证明 定理要求证明
per A=p[i1,i2,…ik|j11,j12,…j1k] ·p[i1,i2,…ik|j11,j12,…j1n-k] +…+p[i1,i2,…ik|jt1,jt2,…jt1k] ·p[i1,i2,…ik|jt1,jt2,…jtn-k] (3)
其中,p[i1,i2,…ik|j11,j12,…j1k],…,p[i1,i2,…ik|jt1,jt2, …jt1k]是per A中选定第i1,i2, …,ik行后得到的所有k阶子积和式,根据引例1 p[i1,i2,…ik|jp1,jp2, …jpk] ·p[i1,i2, …ik|jp1,jp2,…jpn-k]中每一项都是per A中一项,而且当 p≠q时,p[i1,i2, …ik|jp1,jp2, …,jpk]与 p[i1,i2, …ik|jq1,jq2,…,jqk]至少有一列不同,故
p[i1,i2,…ik|jp1,jp2,…jpk] ·p[i1,i2,…ik|jp1,jp2, …jpn-k]和 p[i1,i2, …ik|jq1,jq2,…jqk] ·p[i1,i2,…ik|jq1,jq2,…jqn-k]无公共项.因此为了证明定理,只需证明等式 (3)两边项数相等就可以了.显然等式左边共有n!项,即我们只需证明 (3)式右边也有n!项.为了计算右边的项数,首先来求出t.根据子积和式的取法可知
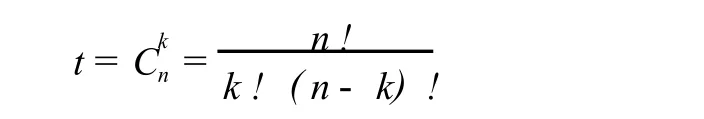
因为 p[i1,i2,…ik|jp1,jp2, …jpk]中共有k!项,p[i1,i2, …ik|jp1,jp2, …,jpn-k]中共有 (n-k)!项,_所以右边共有k!(n-k)!_=n!项.定理得证.
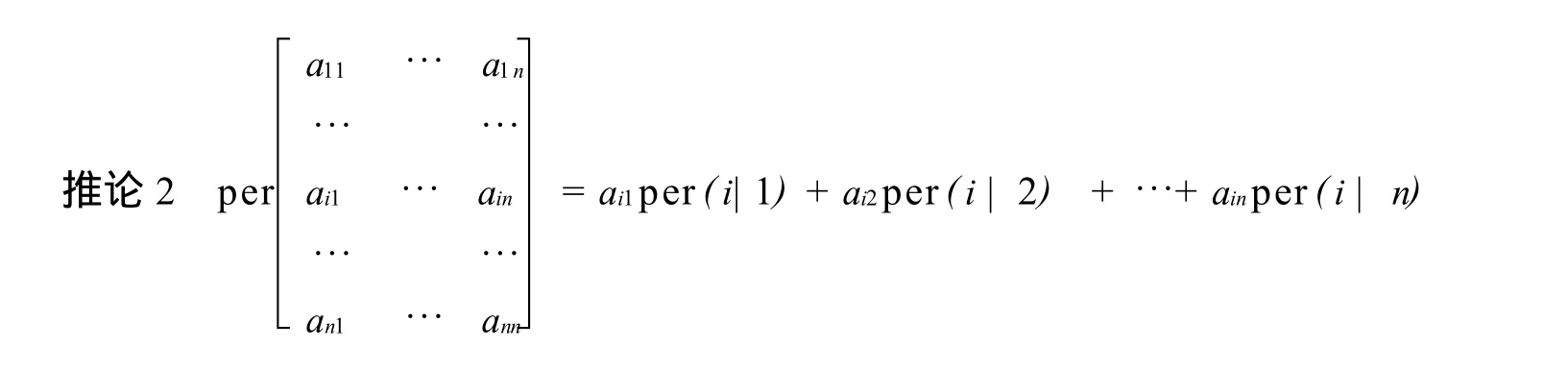
3 应用举例

即对于任意 n≥2,都有 Δn=x·Δn-1+an(n≥2),
因此
Δn=x·(x·Δn-2+an-1) +an=x2·Δn-2+an-1x+an=x2·(Δn-3+an-2) +an-1x+an…………=xn-1Δ1+a2xn-2+…+an-1x+an,但Δ1=per(x+a1) =x+a1,故per A=Δn=xn+a1xn-1+…+an-1x+an.
[1] Bhatia R,Elsner L.On the variation of permanents[J].Linear Multil Algebra,1990,27:105-110
[2] 王恒亮,汤秀芳.积和式的性质与应用 [J].通化师范学院学报,2006,(04):10-12
[3] 李建平,谢冬长.一类 (0,1)-矩阵的积和式 [J].广东工业大学学报,2009,(03):92-95
[4] 扈生彪.(0,1)-矩阵的积和式的图表示及其相关性质 [J].数学进展,2005,(02):160-166

