具有反馈控制的基于比率的三种群捕食模型的渐近性
郑秀亮,韩振芳,徐永春
(河北北方学院理学院,河北张家口075000)
0 引 言
大量的文献研究了种群的持久生存与全局渐近性[1-5].Fan等[6]讨论了一类基于比率的两种群非自治捕食模型的动力学状态,CHen等[7]讨论了一类基于比率的具有反馈控制的两种群非自治捕食模型的持久性、全局渐近稳定性及正概周期解[8]的惟一渐近稳定性.在此基础上,本文研究一类具有反馈控制的基于比率的三种群捕食模型的持久生存与全局渐近性,模型如下:
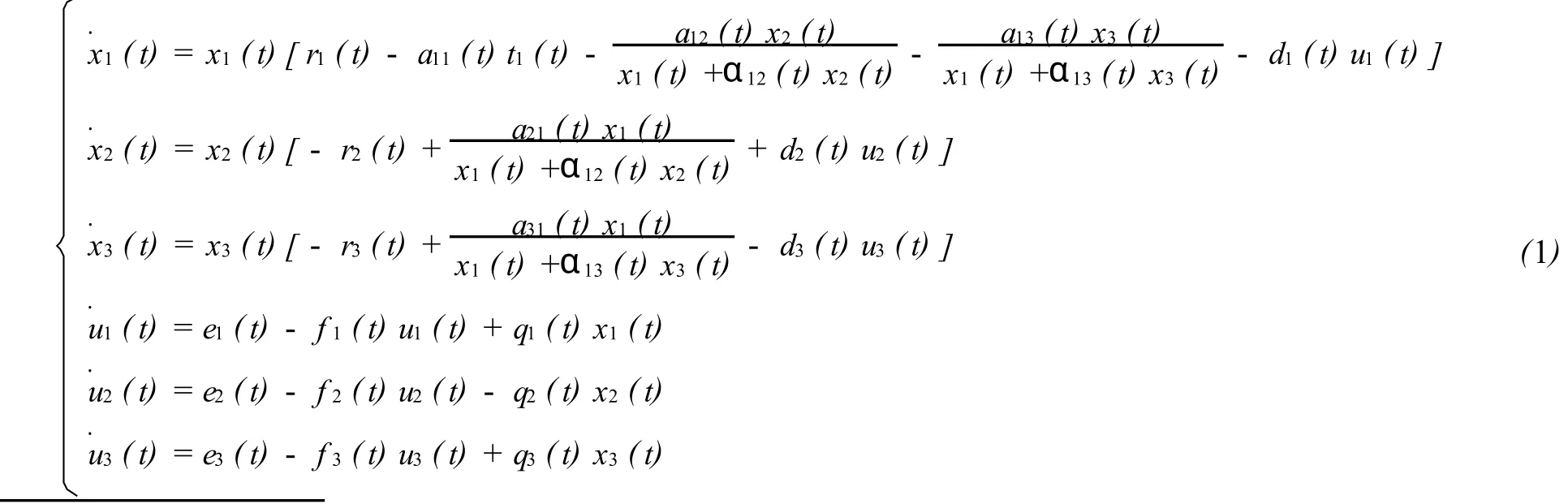
其中xi(t)(i=1,2,3)分别表示种群 Xi(t)(i=1,2,3)在时刻t时的密度,ui(t) (i=1,2,3)表示控制变量,系数 ri(t),di(t),ei(t),fi(t),qi(t) (i=1,2,3),a1i(t) (i=1,2,3),ai1(t) (i=2,3),α1i(t)(i=2,3)均有连续正的有界函数,为方便起见,对任意连续有界函数 g(t)引入记号

考虑到生态意义,故假定模型 (1)满足初始条件 xi(t0) >0,ui(t0) >0的解 xi(t)>0,ui(t)>0(i=1,2,3).
本文分如下三部分:第一部分证明了模型 (1)的一致持久性,包括定理1和定理2;第二部分证明了当模型 (1)为周期模型时,其正周期解的全局渐近稳定性,包括定理3与定理4;第三部分通过实例分析验证了定理2与定理4的可实现性.
1 模型 (1)的一致持久性
定理1 假设模型 (1)满足下列条件

则Ω是模型 (1)的正不变集.其中
Ω={(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))T|mi≤xi(t)≤Mi,mi+3≤ui(t)≤Mi+3(i=1,2,3)}

证明 设(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))是模型 (1)满足初始条件mi≤xi(t0)≤Mi,mi+3≤ui(t0)≤Mi+3,(i=1,2,3)的解,由模型 (1)的第一个方程得
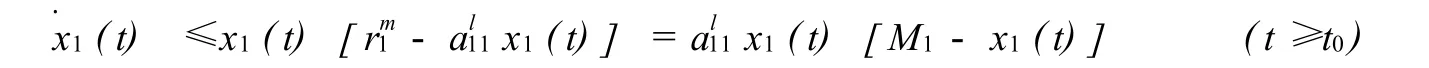
利用比较原理得
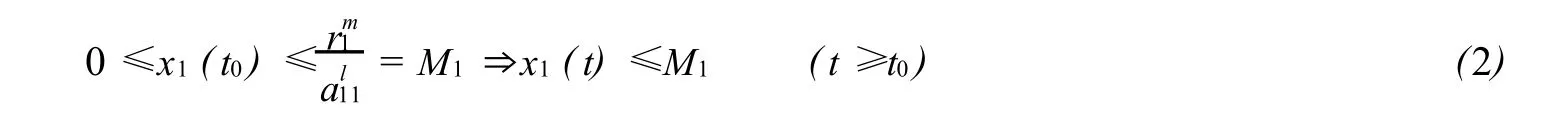
由模型(1)的第三个方程结合(2)与第五个方程得
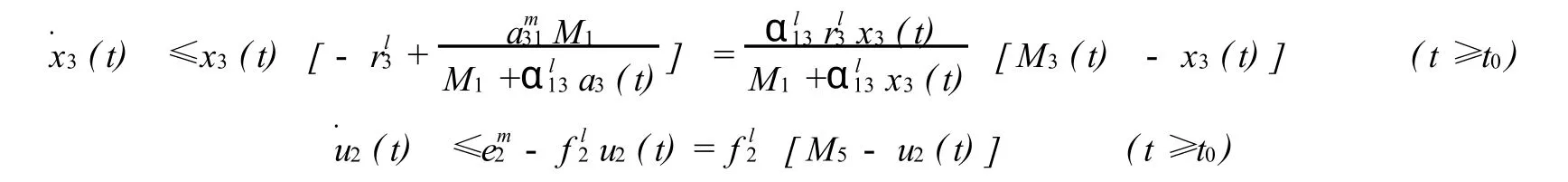
利用比较原理得

由模型(1)的第二个、第四个、第六个方程分别与(4)、(2)、(3)结合得
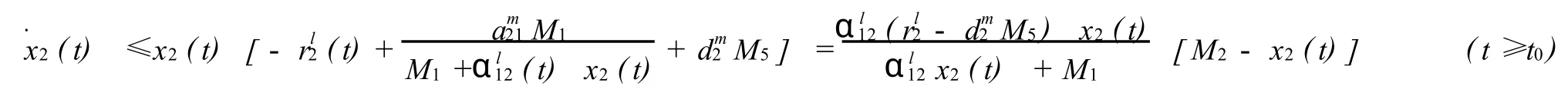
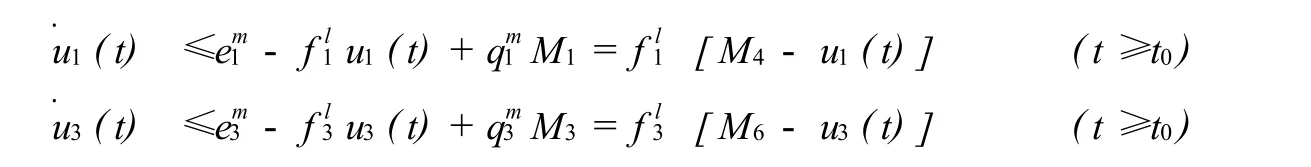
利用比较原理得

另一方面,利用同样的方法有

定理1证毕.
因此由上面证明过程可得定理2.
定理2 假设模型 (1)满足条件 (H1)-(H3),则Ω是模型 (1)的最终有界域,从而模型 (1)是持久生存的.
2 周期解的全局渐近性
在以下的讨论中,假定模型 (1)中所有系数均为时间t的具有正ω-周期的连续函数,则模型 (1)称为一个ω-周期模型.设 X=(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))∈R6+,||X||=|x1(t)|+|x2(t)|+|x3(t)|+|u1(t)|+|u2(t)|+|u3(t)|,在 D⊂R6+定义 Poincare映射,由不动点定理[10]和定理2可得定理3.
定理3 若ω-周期模型 (1)满足条件 (H1)-(H3),则模型 (1)至少存在一个严格正的ω-周期解.
定理4 若ω-周期模型 (1)满足条件 (H1)-(H3)及下列条件
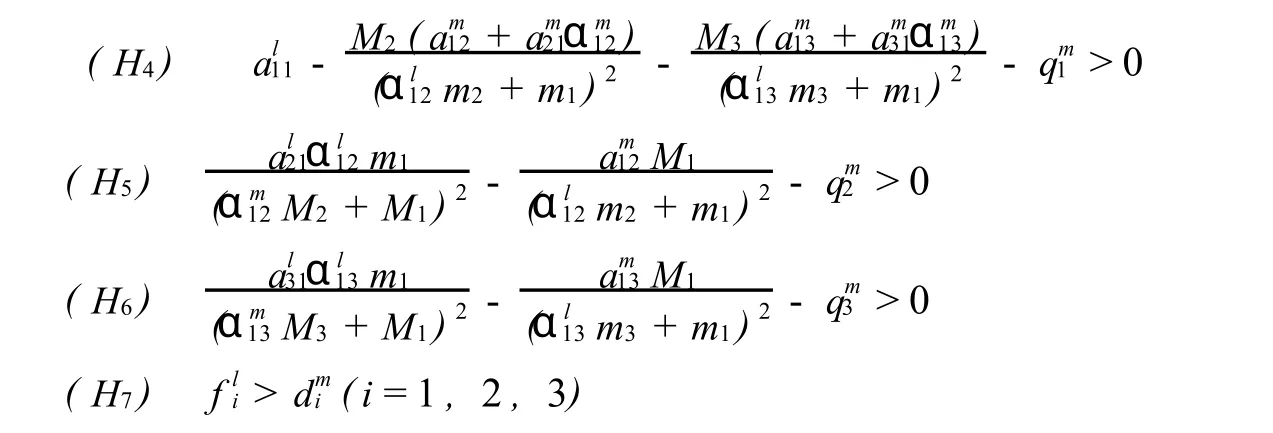
则模型 (1)存在惟一全局渐近稳定的正ω-周期解.
证明 设 X(t) =(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))是模型 (1)的一个严格正的周期解,Y(t) = (y1(t),y2(t),y3(t),v1(t),v2(t),v3(t))是模型 (1)任意满足初始条件 xi(t0)>0,ui(t0)>0(i=1,2,3)的解.构造Lyapunov函数

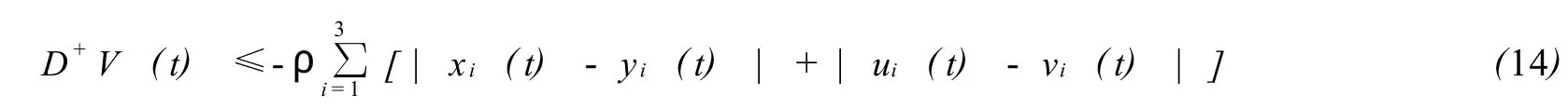
由 (14)式两端在 [T,t](T≥t0)上积分得

注 Chen等[7]的主要结论是本文结论a13(t) =α13(t) =r13(t) =a31(t) =d3(t) =e3(t) =f3(t) =q3(t) =0的特殊情况.
3 实例分析
本部分举例通过数值计算说明定理2与定理4的可实现性,考虑模型(1)满足如下条件


由上面计算可知条件 (H1)- (H7)成立,根据定理2模型 (15)是持久生存的,根据定理4模型(15)有惟一全局渐近稳定的周期解.
[1] Freedman H I,Shukla JB.The effort of a predator resoure on a diffusive predator-prey system[J].Nature Resource Modeling,1989,3(03):359-383
[2] Chen SY,Tang HJ.Persistence and periodic solutions for predator-prey model with dispersal[J].Southeast Asian Bullet Math,2004,(27):989-994
[3] Yu SX,Sun CL.Persistence and global stability for nonautonomous predator-prey system diffusion and time delay[J].Comp Math Appl,1998,35(06):33-40
[4] 陈斯养,黄健科.具有反馈控制的两种群竞争系统的渐近性 [J].陕西师范大学学报:自然科学版,2007,35(01):21-24
[5] 田亚品,陈斯养.具有反馈控制的三种群捕食系统的持久性 [J].云南师范大学学报:自然科学版,2006,26(06):3-8
[6] Fan M,Wang Q,Zou X.Dynamics of nonautonomous ratio-dependent predator-prey system[J].Proc Royal Soc Edinb A,2003,133(02):97-118
[7] Chen C,Ji K.On a nonautonomous ratio-dependent predator-prey system with feedback controls[J].J Biomath,2007,22(02):200-208
[8] Yoshizawa T.Stability theory and the existence of periodic solutions and almost periodic solutions[M].New York:springer-verlag,1975:210-223
[9] Barbalat I.System equations differentielled oscillations nonlieaires[J].Rev Roum Mathp App l,1959, (04):267-270
[10] Yu SX,Sun CL.Persistence and periodicorbits for two-species predator-prey system with diffusion[J].Canada Quart App Math,1998,6(03):223-244

