利用聚类分析方法研究储层流体类型
刘海洲,王勇军,邢鹏举,张荣莉,伍妍红
(1.中国石油集团川庆钻探工程公司测井公司,重庆400021;2.中国石油集团川庆钻探工程公司长庆固井公司,陕西西安710021;3.中国石油集团测井有限公司长庆事业部,陕西西安710201;4.中国石油集团测井有限公司华北事业部,河北任丘062552)
0 引 言
聚类分析通过建立数学模型定量描述某一样本空间中样本点的亲疏关系[1-2]。应用到测井评价中,就是针对某一油气田或构造的勘探目的层,利用测井、岩屑、录井、岩心、试气等各种有用信息,以多参数构建1个样本空间来观测储层。应用聚类分析方法绘制储层的分类图,将已经过测试检验的储层标注在储层分类图上,按聚类算法原理,以储层分类图上样本点的亲疏关系来预测未试气储层流体类型。聚类分析方法目前应用于测井评价主要是储层类型的划分,①裂缝型和非裂缝型储层的划分;②有效的孔隙型储层和干层的划分。储层流体类型判别成功的实例不多,这限制了聚类分析方法的应用范围。
纵观各聚类分析方法和超空间上点间距的算法可知,聚类分析自身不存在应用层面的局限问题,关键是样本空间的构建,一方面,建立的样本空间是否真实客观地反映了储层信息;另一方面,表征的信息是否明确表达了所需的目标。本文通过扩展并优化样本空间观测参量来拓展聚类分析在储层评价中的应用领域。该方法经过川中地区某裂缝、孔、洞并存,基岩孔隙度低、裂缝影响大,空隙结构、气水关系复杂构造上的26口井测试检验,应用效果明显。
1 数学模型
聚类分析方法应用到储层评价,关键是构建合理的样本空间和聚类分析方法的优选。
1.1 样本空间的建立
以拓展测井、岩屑、录井、气测、岩心、试气等信息应用范围为目的,以测井和统计学相关理论为基础,构建1个以储层多参数为观测对象的样本空间。多个储层组成的集合记为 X={X1,X2,…,Xi,…, Xn},单个储层 Xi(或样品)有 p个观测参量,记为Xi={xi1,xi2,…,xij,…,xip}:第 i个样品的第 j个观测参量为xij。这样,就建立了一个以储层多参数作为观测指标的 p维样本空间,原始资料矩阵为[3]

根据以上定义可知,(xi1,xi2,…,xij,…,xip)是p维样本空间上的1个点。
1.2 样本点距离的计算
点与点之间距离的计算方法有欧氏距离、相似系数(变量矢量的余弦 Cosine)、皮尔森相关系数(Pearson correlation)、切比雪夫距离、绝对值距离、明氏距离等。点与点之间距离的计算支持自定义距离,它是1个绝对幂的度量,即变量之差绝对值的q次之和的r次根,q与r由用户指定。距离和相似计算公式见表1[4-5]。

表1 点间距计算方法列表
采用以上任意一种求取 p维样本空间点间距的方法,可以得到点间距第1级矩阵D(1)。需要说明的是,在 p维样本空间点里,点间距满足:①任意一点与自身距离为0,记为:Dij=0;②2点间的距离从不同的角度计算恒等,记为 Dji=Dji。所以,构建点间距第一级矩阵D(1)可以写成下三角形式,但包含了所有点间距的信息[3]

聚类的基本思路:首先,将 n个样品看成n类,即1类只包括1个样品,然后将性质最接近的2类合并成1个新类,这样就得到了 n-1类,再从 n-1中找出性质最接近的2类加以合并,变成n-2类,按此继续下去,直到所有的样品全在一类为止[3]。
根据表1提供的求点间距公式(2)获得n-1类的情况。根据类与类之间的距离定义不同,也产生了7种不同的系统聚类方法:最短距离法、最长距离法、重心法、中间距离法、类平均法等(见表2)[3,6]。
在聚类分析过程中,聚类方法不同聚类的结果也会有一些差异。因此,作聚类分析时应多选用几种以找出共性的结果,对一些有争议的可以结合背景知识,通过判别分析来解决。
1.3 储层聚类分析的理想模型
对于任意一个储层 Xi有p个观测指标,即点(xi1,xi2,…,xij,…,xip)在 p维的样本空间里。储层(或样品)有 n个,空间上的点集可以记为{X1, X2,…,Xi,…,Xn},通常,需要将储层分为气层、气水层、水层和裂缝型储层等多种类型,按照此要求,在p维空间上的理想分类模型见图1。
假设建立的样本空间有很强的针对性,既能反映了储层的物性好坏,也能反映储层的流体类型,而具有相同流体类型的样本点在 p维空间上表征出的性质必然接近,那么,同为气层的数据点就会聚成一类,同为水层的也会聚成一类,将已测试的储层在储层分类图上进行标定,按聚类算法原理,根据储层分类图上的亲疏关系即可预测未试气储层流体类型,并参考测井解释结论。理想的储层聚类分类见图2。
2 储层亲疏关系参量的计算分析
川渝地区某构造上的雷口坡组储层在横向上分布比较稳定,但气水关系复杂,采用常规测井数据建立样本空间。因为某一储层的测井项R为一单列数组,对于任意某一测井项R(如GR、AC、Rt、CNL…),测井储层评价的主要任务是挖掘R值的大小和幅度变化信息来完成储层评价任务。那么,聚类分析样本空间所构建的观测参数必须反映R值的大小和幅度变化这2个方面的情况。因此,设置4个统计参数,分别为最大值 Rmax、最小值 Rmin、极差 Rrange、均值 Rave表征其值的变化量;设置另外3个参数,标准差 RStd、偏度 Rsks、峰度 RKurtosis反映其幅度变化情况。

表2 类间距计算方法列表
假设储层流体类型信息包含在测井量 GR、AC、CNL、DEN、Rt、Δtc、Δts等7个参数里,每个测井项再扩展上述7个参数综合反映其值的大小和幅度变化情况,这样,就构建了一个 p=7×7=49维样本空间;然后,逐一把单井雷口坡储层对应的数据点置于49维的样本空间进行聚类分析。该实例采用自定义距离(custom)计算点间距、类平均法(Betweengroups linkage)计算类间距,聚类数上限设置为8,就可以得到第1级分类表(见表3)、储层流体类型分类图(见图3)以及第1级聚类矩阵。
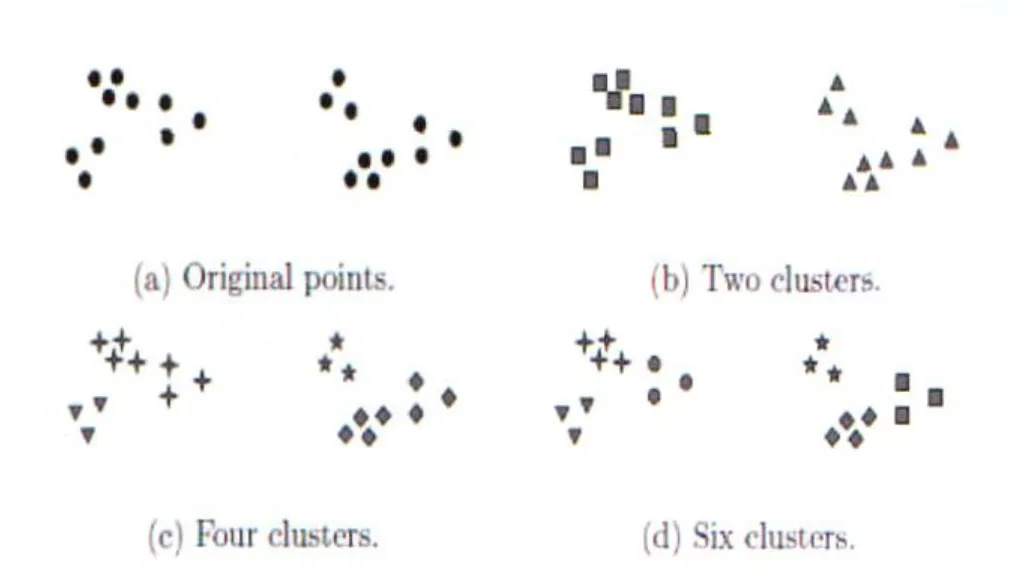
图1 p维空间上数据点聚类模型图
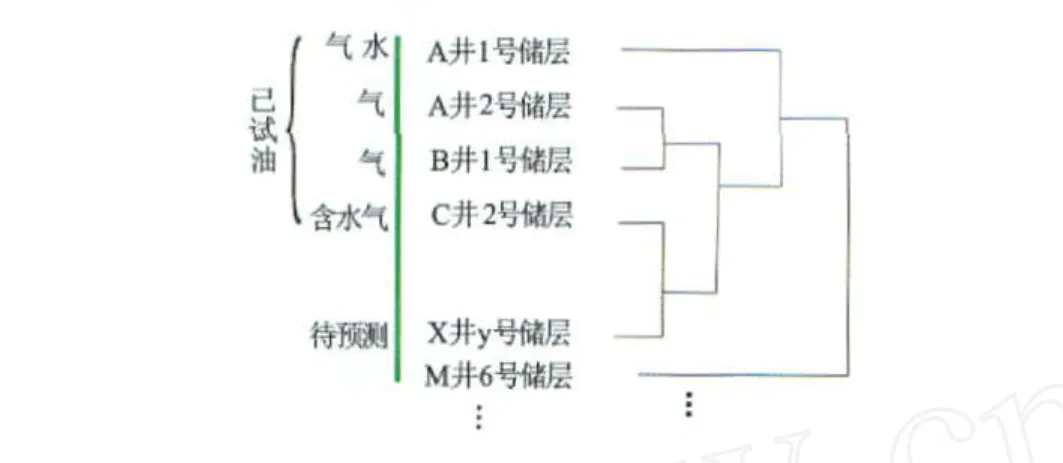
图2 理想的储层聚类分类图
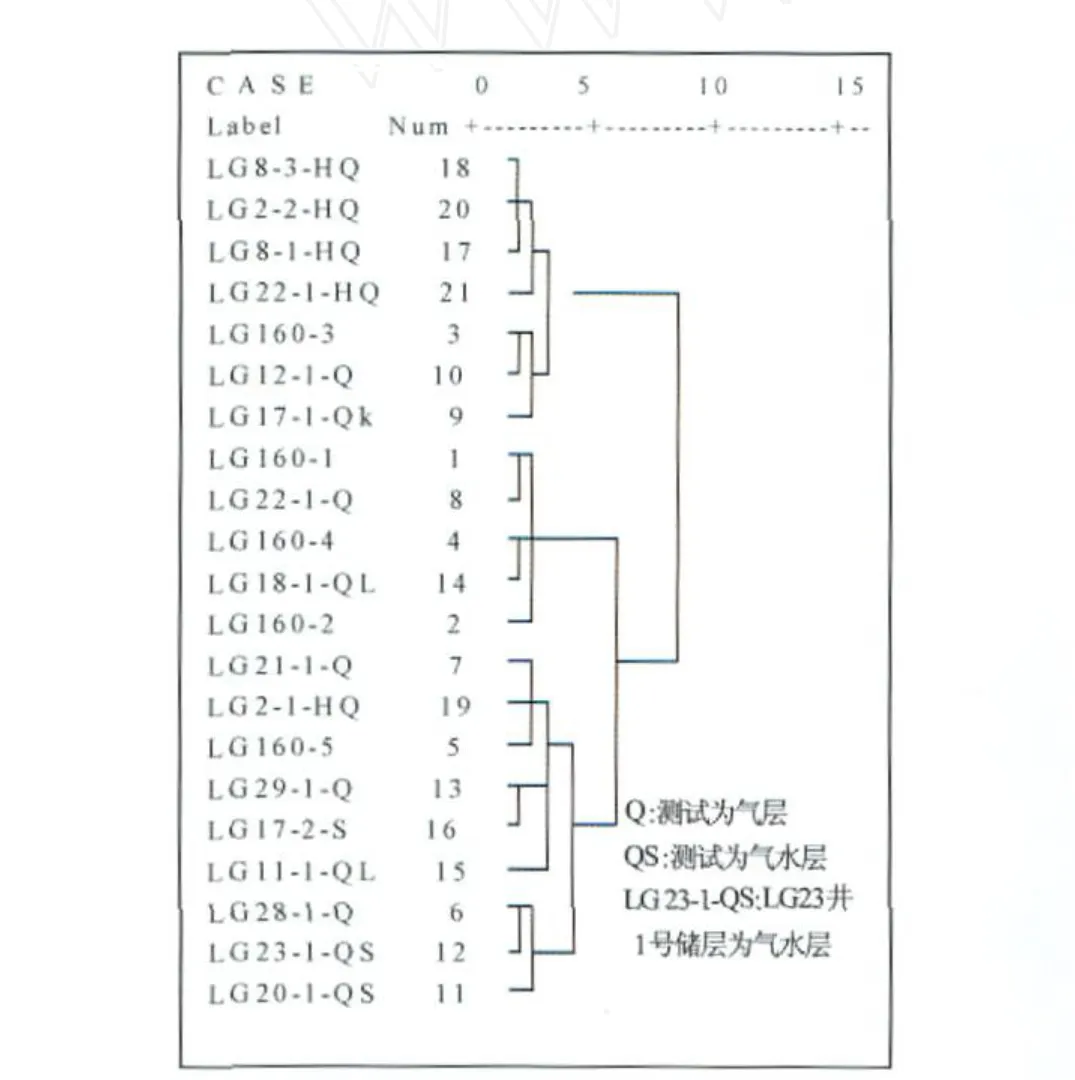
图3 储层流体类型分类图

表3 第1级分类表
3 应用效果分析
在充分利用测井、岩屑、录井、岩心、试气等各种有用信息,以多参数构建1个样本空间来观测储层的基础上,采用聚类分析方法对该构造26口井进行重新解释,并将新解释结论与试气结果进行对比,解释符合率达到了90%以上,有效地解决了该复杂气水关系储层流体类型的判别问题。
图4是2008年12月所测的该构造L G××井测井综合解释成果图。该井雷口坡组储层射孔井段为3 704~3 751 m,即图4中原解释的1、2、3、4和5号储层,日产气3.659 3×104m3,无水,试气结论为气层。但其中5号解释层的3 750~3 752 m井段岩性为质纯云岩,常规测井资料指示该段孔隙相对较发育,深浅双侧向电阻率低,呈负差异特征,补偿中子孔隙度明显大于声波、密度孔隙度,有较明显的水层特征;微电阻率成像有较明显的裂缝显示,阵列声波纵横波及斯通利波能量有一定衰减,录井无显示,该储层应解释为气水同层。通过聚类综合分析处理,精细解释了该井雷口坡组射孔井段内的储层,扣除了明显的夹层,节约了射孔成本,其中5、6号解释层含水饱和度8%~20%,可动水饱和度为0~3.8%,明显小于8%的水层判别标准,综合解释为气层,与试气结论一致。
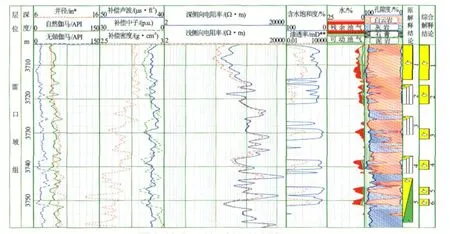
图4 LG××井测井综合解释成果图
4 结 论
在对某一复杂储集空间储层进行流体类型判别之前,应充分利用已有的常规测井、声电成像、岩心、试气等有用信息,正确分析储层的岩性、孔隙空间结构,半定量和定性确定储层类型;针对不同的岩性、不同的储层类型优选与之相适应的流体类型判别方法。聚类分析方法判别川中雷口坡组复杂碳酸盐岩储层流体类型,经过26口井的测试检验,解释符合率大大提高,应用效果明显。
[1] 戴明强,李卫军,杨鹏飞.数据模型及其应用[M].北京:科学出版社,2007:235-247.
[2] 廖觉生,司马立强,赵治春.模糊聚类分析综合判别气水层方法[J].地球物理测井,1991,15(2):100-112.
[3] 高祥宝,董寒青.数据分析与SPSS应用[M].北京:清华大学出版社,2007:311-334.
[4] 赵 宏,谢 航.Q型聚类分析在东北水生植物香蒲属分类研究中的应用[J].水生植物学报,1998,22 (1):86-89.
[5] 罗 利,胡培毅,周政英.碳酸盐岩裂缝测井识别方法[J].石油学报,2001,22(5):31-34.
[6] 董媛媛.模糊聚类分析的2种方法[J].井冈山学院学报,2006,27(6):26-28.

