关于伪余式与子结式的矩阵计算
金 萌
(北京航空航天大学数学与系统科学学院, 信息、数学与行为教育部重点实验室, 北京 100191)
0 引言
伪余式的计算是计算机代数中的基本工具之一,是解多项式方程组的三角分解方法中的基本运算.文献[1]给出了改进算法,李永彬提出了一种利用构造矩阵和高斯消去法来计算伪余式的算法NewPrem[2],NewPrem在计算多元多项式的伪余式时比Maple中已有的算法(prem)效率更高.由于伪余式与特定的矩阵是有联系的,我们试图用线性代数中的Dodgson变换来计算伪余式.子结式和多项式余式序列是多项式代数中计算最大公因子的重要工具之一,关于子结式的研究既有理论上也有算法上的改进工作.例如Docus L给出了一种优化子结式算法[3],优化策略基于多项式余式序列的计算;Abdeljaoued J 等研究了子结式的多种表示形式[4,5];Akritsa A G等提出了一种用矩阵三角化计算子结式的算法[6];李给出了一种用矩阵构造子结式的新算法[7].文献[2]中的结论是促使我们研究用线性代数计算伪余式和子结式的动机.
本文的目标之一是基于李的思想构造一种新的伪余式算法并在Maple中实现;另一目标是对已有的几种子结式矩阵构造算法给出一种统一的描述并将其实现.
1 行列式多项式与伪余式
设R为带单位元的惟一析因整环,而F,G∈R[x]为次数分别为m和n的一元多项式:
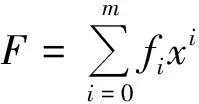
(1)
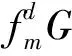
定理1[2]设F,G∈R[x]如式(1) 所示,则prem(G,F,x)=(-1)ndet(A),其中A为(n+1)×(n+1)阶矩阵,第1行元素为G的系数,最后m-1行元素为1和-x,中间n-m+1行元素为F的系数,空白处为零,如下所示
上述定理给出了多项式和矩阵行列式之间的一个联系,这一联系可以推广到多项式与行列式多项式之间,首先需要定义一组多项式的矩阵.
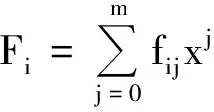
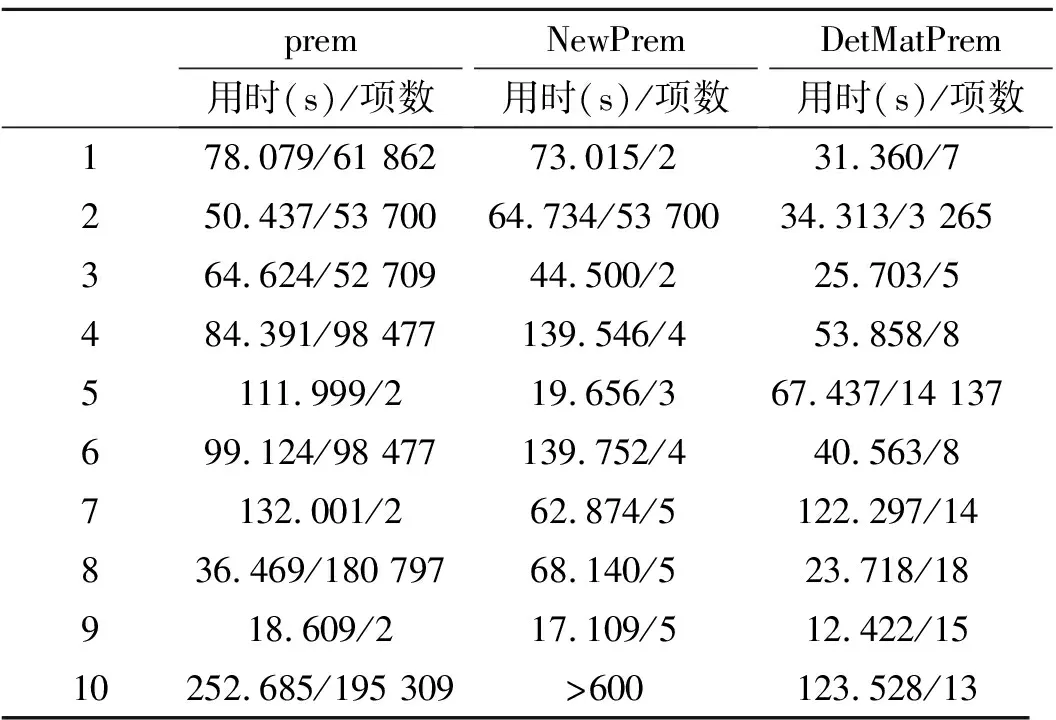
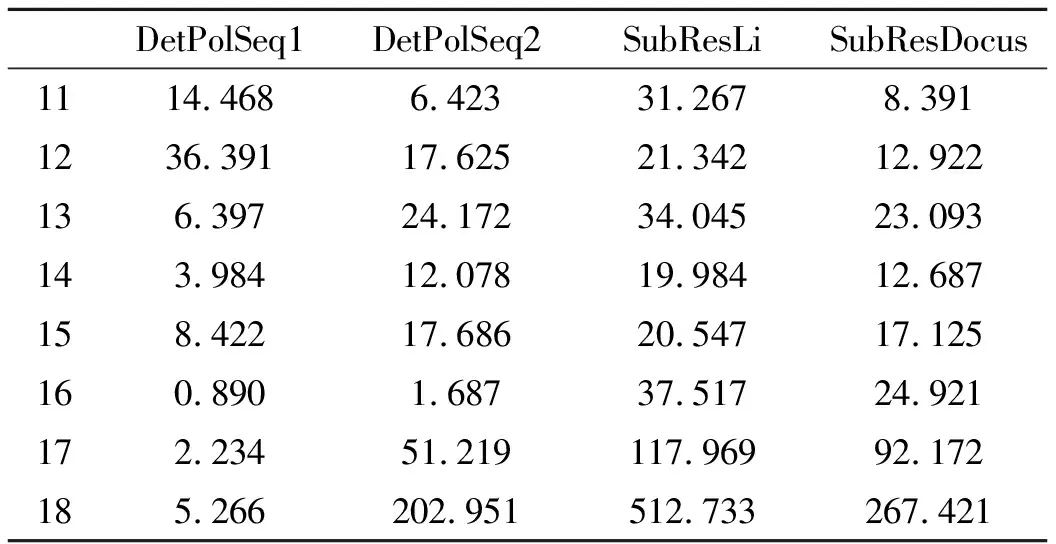
并记为mat(F1,…,Ft).对于任意一组多项式F1,…,Ft,命d:=1+maxi{deg(Fi)},定义F1,…,Ft的矩阵为M=(Mij)∈Rt×d,其中当deg(Fi) 以上是由多项式组定义矩阵,另外我们也可对矩阵定义多项式组. 定义2设t和d为正整数且t≤d,给定矩阵M=(Mij)∈Rt×d,定义M(j)为 (2) 下述定理描述了两个一元多项式的伪余式与行列式多项式之间的联系. 定理2[8]设F,G∈R[x]如式(1)所示,则 prem(G,F,x)=detpol(xn-mF,…,xF,F,G) 称矩阵mat(xn-mF,…,xF,F,G)为G与F的伪余矩阵,并记为matprem(G,F). 现在我们回顾一下线性代数中的Dodgson 变换,见算法1. 算法1(Dodgson) 输入:n×n阶矩阵M=(Mij)∈Rn×n,输出:n×n阶矩阵M′满足条件(3)和(4). 注意,若算法1的输入矩阵M的所有主子式都非零,则不需要改变主元,此时S3和S5.1.1.2可以省略.另外,输出矩阵M′具有如下形式: (3) Dodgson变换的一个重要性质是:当1≤k (4) (5) 利用命题1的证明我们可以构造算法计算伪余式prem(G,F,x),见算法2. 算法2(DetMatPrem) 输入:一元多项式F,G∈R[x],输出:包含伪余式prem(G,F,x)系数的数组[seq(a[m+1-j],j=0..n-1)]. S1.命m:=deg(F,x);n:=deg(G,x). S2.若n S3. 将F,G的系数按照次数降序表示为数组,即命a:=Array(1..n+1,[seq(coeff(G,x,n+1-i),i=1..n+1)]);b:=Array(1..n+1,[seq(coeff(F,x,n+1-i),i=1..n+1)]);(其中Array,seq和coeff都是Maple函数). S4. 对每一1≤k≤m-n+1执行下列步骤:S4.1. 对每一k+1≤i≤m+1执行下列步骤:S4.1.1.a[i]:=b[1]a[i]-b[i-k+1]a[k]. 设t和d为正整数且t≤d,对于矩阵M=(Mij)∈Rt×d,定义Mi×di为M的包含前i行前di列元素的子矩阵,其中1≤i≤t.记Jn为次对角线上元素为1其他位置元素为零的n阶方阵. 定义3设t,d,M如上所示,定义M关于L=[(i1,di1),…,(ir,dir)]的行列式多项式序列为:{detpol(Mi×di):(i,di)∈L},其中1≤i1<… 根据[8],G与F的第i个子结式等于subresi(G,F,x)=detpol(mat(xm-i-1G,…,xG,G,xn-i-1F,…,xF,F)),0≤i 将mat(xm-1G,…,xG,G,xn-1F,…,xF,F)记为M,又将M的行重新排序得到如下矩阵 M′=mat(xn-1F,xn-2F,…,xm-1F,xm-1G,xm-2F,xm-2G,…,F,G) (6) 易证M′关于L=[(k,(m+n+k)/2):k=n-m+2,n-m+4,…,n-m+2m]的行列式多项式序列等于G与F的子结式序列{subresi(G,F,x):i=0,…,m-1}. (7) 另外,对于情形(1)和(3),设detpol(Mi×di)关于x的系数位于第i′行,则 推论2[6]设F,G∈R[x]如(1)所示,并假定deg(G)=n≥m=deg(F).又设M,L如(6)所示,则M关于L的行列式多项式序列,也即G与F的子结式序列{subresi(G,F,x):i=0,…,m-1}可以通过算法1输出的M′得到.(1)若M的所有主子式都不为零,则 上述定理及推论中使用的是Sylvester矩阵的变形,实际上我们同样可以将Bezout矩阵应用Dodgson变换来计算子结式.下面我们介绍Bezout矩阵与混合Bezout矩阵的定义并证明如何应用Dodgson变换来计算子结式序列. 定义4设F,G∈R[x]如(1)所示,定义G与F的Bezout矩阵为(Bij),0≤i,j≤n-1, 其中Bij为式(G(x)F(y)-G(y)F(x))/(x-y)中项xiyj的系数,并记为Bez(G,F). 定义5设F,G∈R[x]如(1)所示,并假定deg(G)=n≥m=deg(F).称按照如下方式构造的矩阵M=(Mij)为G与F的混合Bezout矩阵,并记为HBez(G,F):(1)对于1≤i≤m,1≤j≤n,Mij等于多项式Km-i+1关于xn-j的系数,其中Km-i+1等于(gnxm-i+…+gn-m+i)(fi-1xn-m+i-1+…+f0xn-m)-(gn-m+i-1xn-m+i-1+…+g0)(fmxm-i+…+fi);对于m+1≤i≤n,1≤j≤n,Mij等于多项式xn-iF(x)关于xn-j的系数. L=[(n-m+1,n),(n-m+2,n),…,(n,n)] (8) 证明:只需要证明第2种情形,情形(1)可类似证明.对于i=n-m+1,…,n+m,考虑矩阵Hi×n的行列式多项式,易证 (9) 若H的所有主子式都不为零,即det(Mi×i)≠0,1≤i 下面我们给出计算多项式G与F的行列式多项式序列的算法,即算法3. 算法3(DetPolSeq) 输入:一元多项式F,G∈R[x]满足条件deg(G)≥deg(F),输出:G与F的行列式多项式序列DPS. S1.命m:=deg(F,x);n:=deg(G,x). S2.构造矩阵M(M可以是式(6)或推论3中的B,H)及相应的L. S3. 命M′:=Dodgson(M). S4. 根据式(7)或(9)计算行列式多项式序列DPS. 我们通过实验比较了3种计算伪余式的算法:Maple命令prem、李永彬的算法NewPrem以及本文给出的算法DetMatPrem.实验是在一台CPU为3.2 GHz,内存512 MB的Pentium 4机器上完成的,实验结果如表1所示.表1中的10个例子比较长,这里不再给出,而只给出生成多项式的Maple命令: > G:=randpoly(x,degree=d1,coeffs = proc() randpoly([y,z], degree=d3) end proc); > F:=randpoly(x,degree=d2,coeffs = proc() randpoly([y,z], degree=d3) end proc); 其中在例1~3中,命d1:= 30,d2:= 8,d3:= 6; 例4~6中命d1:= 30,d2:= 10,d3:= 10;例7~9中命d1:= 30,d2:= 20,d3:= 20; 例10中命d1:= 40,d2:= 20,d3:= 10. 表1 伪余式算法比较 需要说明的是上述3种算法的输出多项式都不一定是完全展开的,即没使用Maple命令exapnd.如果使用该命令,那么用时将更多,比如例7,前两种算法在600 s内均没有输出,而DetMatPrem用时仅为132.860 s.由表1可以看出,算法DetMatPrem的效率通常是最高的,对于例3和例7,虽然效率低于NewPrem,但优于prem. 我们比较了4种子结式算法:李永彬的SubResLi、Docus的SubResDocus以及基于(6)的算法DetPolSeq1和基于推论3中的矩阵H的算法DetPolSeq2.实验结果(时间单位为s)如表2所示,表2中的8个例子由如下方式生成: 例11~15: > G:=randpoly(x,degree=d1,coeffs = proc() randpoly([y,z], degree=d3) end proc); > F:=randpoly(x,degree=d2,coeffs = proc() randpoly([y,z], degree=d3) end proc); 例16~18: > G:=randpoly(x,degree=d1,coeffs = proc() randpoly([y,z,w], degree=d3) end proc); > F:=randpoly(x,degree=d2,coeffs = proc() randpoly([y,z,w], degree=d3) end proc); 其中例11、12中命d1:= 7, d2:= 7, d3:= 3;在例13~15中命 d1:= 8, d2:= 4, d3:= 4;例16中命d1:= 5, d2:= 3, d3:= 3;例17中命d1:= 6, d2:= 3, d3:= 3;例18中命d1:= 7, d2:= 3, d3:= 3. 表2 子结式算法比较 由表2容易看出,当参数个数为2且全次数不大时,算法DetPolSeq1和DetPolSeq2比SubResLi和SubResDocus更高效,当参数个数为3时DetPolSeq1是最高效的,尽管Sylvester矩阵比Bezout矩阵复杂. 本文研究了伪余式、子结式与矩阵行列式之间的联系并给出了行列式多项式序列的概念,对用不同类型矩阵构造子结式的算法给出了统一描述,提出了新的伪余式算法DetMatPrem和子结式算法DetPolSeq并在Maple中实现,通过多个随机生成的例子将已有的几种算法进行了比较,实验证明本文提出的算法是高效的. 参考文献 [1] Wang D. A generalized algorithm for computing characteristic sets[C]. Computer Mathematics: Proceedings of the Fifth Asian Symposium (ASCM 2001), Matsuyama, Japan, 2001. [2] Li Y B. An alternative algorithm for computing the pseudo-remainder of multivariate polynomials[J]. Applied Mathematics and Computation, 2006, 173(1):484-492. [3] Ducos L. Optimizations of the subresultant algorithm[J]. Journal of Pure and Applied Algebra. 2000, 145(2): 149-163. [4]Abdeljaoued J, Diaz-Toca G M, Gonzalez-Vega L. Bézout matrices, subresultants and parameters[C]. MACIS 2007, 2007. [5] Hou X, Wang D. Subresultants with the Bézout matrix[C]. In:Computer Mathematics-Proceedings of the Fourth Asian Symposium(ASCM 2000), Singapore New Jersey, 2000: 19-28. [6] Akritas A G, Akritas E K, Malaschonok G I. Matrix computation of subresultant polynomial remainder sequences in integral domains[J]. Reliable Computing,1995, 1(4): 375-381. [7] Li Y B. A new approach for constructing subresultants[J]. Applied Mathematics and Computation, 2006, 183(1):471-476. [8] Mishra B. Algorithmic Algebra[M]. Springer, 1993. [9]Von zur Gathen J, Lucking T. Subresultants revisited[J]. Theoretical Computer Science, 2003, 297(1-3): 199-239.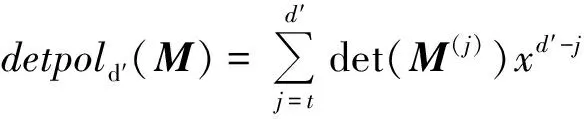
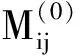
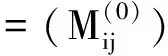
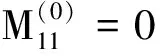
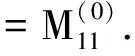
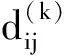
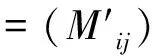
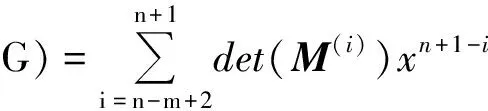
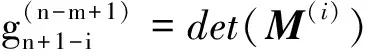
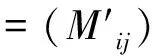
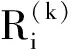
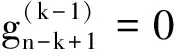
2 行列式多项式序列
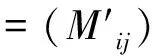
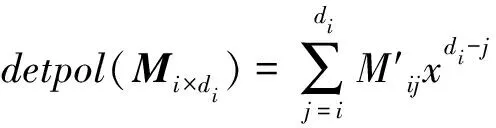
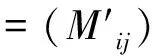
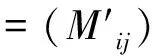
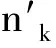
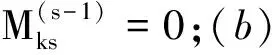

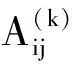
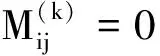
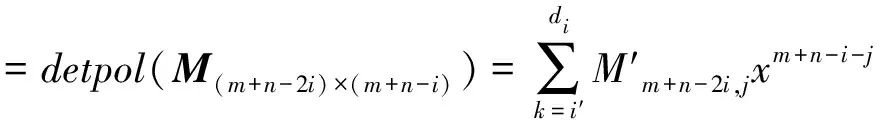
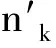
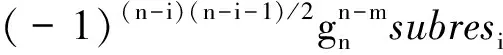
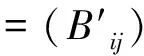
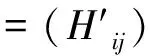
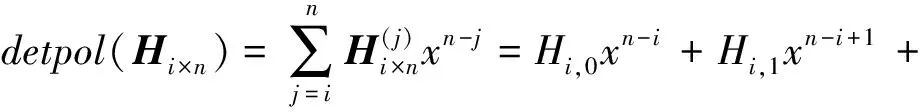
3 实验结果
3.1 伪余式的计算
3.2 子结式序列的计算
4 结束语

