齿轮箱传感器优化布置研究

魏秀业，潘宏侠，黄晋英

(中北大学 机械工程与自动化学院，山西 太原030051)

传感器的优化布置是齿轮箱监测系统中重要的问题，应该做到使用尽量少的传感器获取尽可能多的结构信息。在国内外现有的对传感器优化布置研究中，对于桥梁监测系统传感器优化布置研究较多，而对于齿轮箱这类复杂的机械设备传感器优化布置的方法研究甚少。文献［1 -5］将优化传感器用于模态测试和参数识别、故障检测中，文献［6］用主元分析法优化传感器布置用于过程监控。智能的优化算法是近几年发展起来的模拟生物和物理过程的方法，在传感器布置中占有重要的地位，其中以遗传算法应用和研究最为广泛［7］，它弥补了传统的优化算法的很多不足。粒子群算法是一种基于群体智能理论的全局优化算法，其采用实数编码，避免了遗传算法复杂的操作过程，简单易实现，目前围绕提高收敛速度、避免早熟等进行了多种算法改进，已经取得一些研究成果，并在一些领域得到应用。由于粒子群优化(PSO)算法在解决优化问题上有其明显的优势，本文将针对齿轮箱信号采集过程中传感器布置数量难以估计和定位困难的现象，将PSO 算法引入到齿轮箱状态检测和故障诊断的传感器优化问题上，提出以目标函数作为优化的依据，应用改进的动态加速常数的PSO 算法解决传感器测点的选择和优化问题。

1 加速度自适应粒子群优化算法

通常基于种群的优化方法，在优化的早期应该鼓励粒子在整个搜索空间移动，而不是聚集于局部极值的周围。另一方面，在优化的后期，提高趋于最优解的收敛率而有效地找到最优解是非常重要的。考虑到这些相关因素，在标准PSO 算法的基础上，提出动态的加速常数作为一种新的参数自适应策略，以下将动态加速常数的PSO 算法，称为加速度自适应粒子群优化(CPSO)算法.

这种改进，即在标准PSO 算法中，即(1)式、(2)式，实现加速常数c1和c2随进化代数线性地改变，如(3)式和(4)式。

当vid＞vmax时，取vid=vmax;当vid＜-vmax时，取vid=-vmax，

(1)式～(4)式中:i=1，2，…，m 为组成群体的粒子数;d=1，2，…，D 为目标搜索空间的维数;加速常数c1和c2为非负常数;r1和r2为服从［0，1］上的均匀分布的随机数;xid(t)为第i 个粒子的当前位置;pid为第i 个粒子迄今为止搜索到的最优位置;pgd为整个粒子群搜索到的最优位置;vid为第i 个粒子的当前速度vid∈［-vmax，vmax］;vmax为最大限制速度，是非负数;R1、R2、R3、R4是初始设定的定值;t、tmax分别为当前进化代数和最大进化代数;ω 为惯性权重，一般取ω=ωmax-(ωmax-ωmin)t/tmax.

将该算法在神经网络中进行测试，通过仿真实验［8］，综合比较发现，应设定0＜R1+R2≤2，进化曲线具有收敛速度较快的特点。因为2 者的数值过大不利于微粒的开发，其中R1也不可过小，太小则在最初的速度进化迭代中单个粒子优化作用得不到体现;应设定R3-R4≥2，R3适当加大以提高空间搜索能力来获得合适的种子，考虑到速度的取值范围R3-R4之差不宜过大，这样粒子群搜索初期有较好的探索新空间的能力，随着迭代的进行线性减小，而局部搜索的能力线性增加，加大局部开发能力以得到最优值。

2 PSO 算法在齿轮箱测点优化中的应用

2.1 PSO 算法传感器布置的适应度

测点选择问题实际上是一种满足一定准则或目标的优化问题。PSO 算法是近十年来发展起来的随机搜索的优化算法，粒子群在搜索进化的过程中直接用适应度来评价解的优劣，并以此作为以后搜索的依据。考虑到齿轮箱监测过程主要使用的传感器是加速度计，并考虑到齿轮箱结构的特点，在选择传感器最优布点时，设计了基于模态置信准则(MAC)的适应度。

文献［9］认为MAC 矩阵是评价模态向量交角的一个很好的工具。由结构动力学原理可知，结构各固有振型在节点上的值形成了一组正交向量。但由于量测自由度远小于结构模型的自由度并且受到测试精度和测量噪音的影响，测得的模态向量已不可能保证其正交性。在极端的情况下甚至会由于向量间的空间交角过小而丢失重要的模态。因此，在选择测点时有必要使量测的模态向量保持较大的空间交角，尽可能地把原来模型的特性保留下来。模态置信度MAC 矩阵经常用于对试验振型和理论振型进行匹配和比较，它非常容易实施并且不需要结构的质量矩阵和刚度矩阵，MAC矩阵表示为

式中:φi和φj分别为第i 阶和第j 阶模态向量。

MAC 矩阵非对角元素应介于0 和1 之间，小于0.25 表示2 个模态向量较易分辨，等于0 表示2 个模态向量相互正交，因此在传感器优化布置过程中，应该尽量使MAC 矩阵非对角元素最小，即

因此，可将(6)式作为测点优化的适应度函数。

2.2 齿轮箱有限元建模和模态计算分析

以图1所示的实验室JZQ250 齿轮箱作为测点优化对象，为了建立传感器优化的适应度函数，必须对其进行有限元建模和模态计算，然后以有限元分析和模态计算结果为依据，根据(5)式和(6)式构造MAC 矩阵，即适应度函数，以此目标函数作为粒子群进化过程中评价解的优劣的依据。

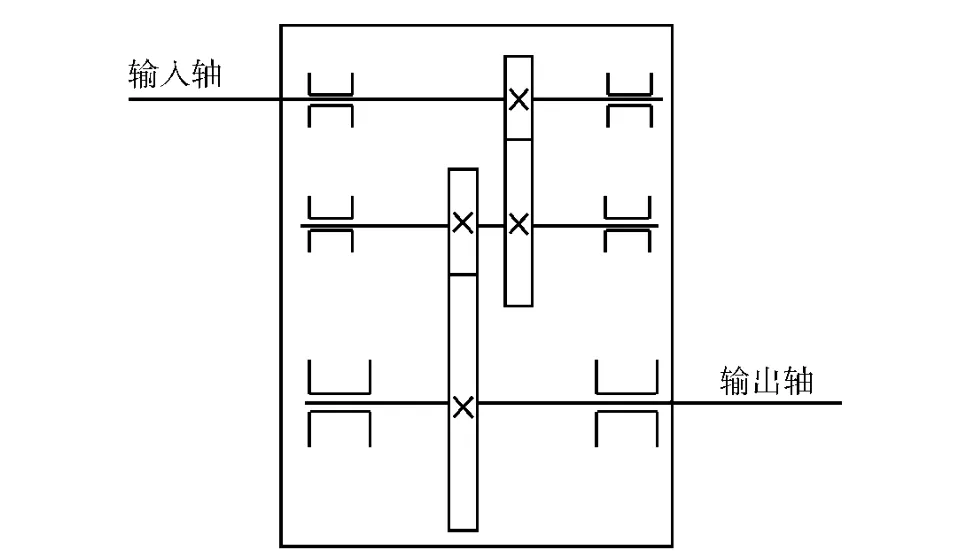
图1 JZQ250 齿轮箱传动示意图Fig.1 Sketch of JZQ250 gearbox transmission

齿轮箱体由上下2 个半箱体组成，上箱体尺寸为540 mm × 230 mm × 168 mm，下箱体尺寸为540 mm×230 mm ×160 mm，主体部分为铸件，材料采用HT21-46，箱体质量51.3 kg.采用美国的三维PRO_ E 软件进行三维实体建模，然后导入ANSYS10.0进行齿轮箱的有限元分析计算和模态分析。

齿轮箱体共划分为15 033 个节点，采用8 节点四面体SOLID 45，单元数为55 163 个。根据齿轮箱体的实际工作情况，将其底板的安装固定部位处4个节点的自由度全部约束，作为整个模型的边界条件，得到的有限元模型，如图2所示。

图2 JZQ250 齿轮箱体有限元模型Fig.2 Finite element model of JZQ250 gearbox

研究中共计算20 阶固有频率，剔除局部模态，共计算了10 阶箱体的固有频率和振型，模态计算结果如表1所示。图3为第1 阶典型振型图，第1阶振动频率为48.81 Hz，大体沿轴向摆动。从齿箱的模态分析可以看出上箱体的振动远比下箱体的振动大。

2.3 初选点方案

初选点方案是优化的约束条件，由2.2 节分析知齿轮箱上箱体的振动远比下箱体的振动大，且上箱体各阶模态较为密集，因此测点的布置原则是保证可以激发出齿轮箱体的各阶模态，对于轴承座等重要部位以及能够引发噪声比较大的部位采取多布点。所以理论上在上箱体初选10 个测点，并在箱体上标出各测点位置，并逐一对其进行编号。测点布置位置及编号和对应的有限元节点，如图4所示。初选10 测点前8 阶总模态位移由2.2 节有限元建模和模态计算结果得出，如表2所示。对初选的10个测点进行分析。

表1 齿轮箱体的计算模态固有频率及振型Tab.1 Inherent frequency and vibration type of gearbox case

图3 齿轮箱体一阶模态振型Fig.3 First modal vibration type of gearbox case

图4 齿轮箱盖测点初始化布置图Fig.4 Initial layout of test points in gearbox cover

2.4 CPSO 的实现过程

1)将测点数作为粒子，通过(5)式、(6)式构造函数f，并将其作为粒子群优化的适应度函数。

2)给定粒子的取值范围［1，10］，设定CPSO 的种群粒子数m、最大进化代数tmax，实现加速常数自适应变化的常数R1，R2，R3，R4，惯性权重的最大值、最小值ωmax，ωmin，粒子飞行的最大限制速度vmax.具体取值如表3所示。

表2 测点各阶总模态位移Tab.2 Total modal displacement of different orders in test points

3)随机产生粒子初始群体，且随机初始化种群中每个粒子的位置和速度，计算个体的适应度fp和种群的整体适应度fg.

4)比较粒子的当前适应度fp和自身最优值fpbest.如果当前值fp比fpbest更优，则置fpbest=fp，并设fpbest位置为D 维空间中的当前位置。

5)比较粒子适应度与种群适应度最优值fgbest.如果当前值fpbest比种群fgbest更优，则置fgbest为当前粒子的矩阵下标和适应度。

6)判断迭代次数t 是否达到终止条件。如果t＜tmax，重复步骤3)～5);否则将当前解作为最优解输出，算法终止。

2.5 优化结果及分析

以齿轮箱模态分析的8 阶振形的10 个测点进行研究，初选10 个测点的不同阶模态总位移作为输入数据，如表2所示，以适应度即MAC 矩阵非对角元素最大值MACmax作为优化对象，以测点数为粒子，应用CPSO 算法进行传感器位置寻优，CPSO 算法的参数设置如表3所示，适应度随不同传感器数量变化曲线，如图5所示，不同测点数对应的最小适应度和相应的传感器的布置位置，如表4所示。

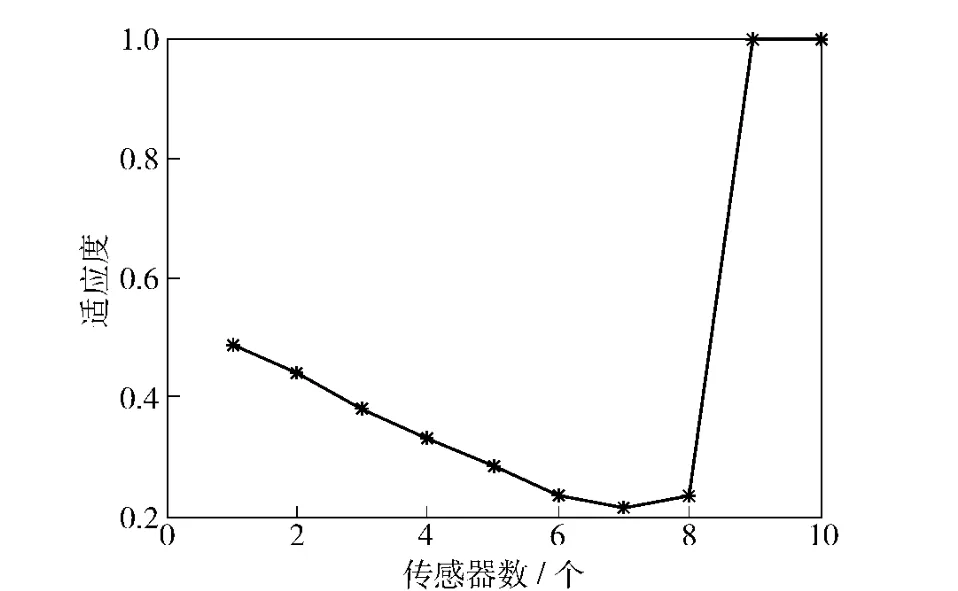
图5 适应度随传感器数量变化曲线Fig.5 Fitness varying with number of sensors

1)从表4可以看出:MAC 矩阵的非对角元的值随着测点数的增加而减少，当测点数为6、7、8 时，MACmax的值小于0.25，也即此时，选择的测点数使量测的模态向量保持较大的空间交角，尽可能地把原来模型的特性保留下来。且从图5适应度(MACmax)随传感器数量变化曲线来看，当测点数为7 时，MACmax的值最小为0.213 86，当测点增加到9时，MACmax值反而增大到1，说明在这种情况下，模态向量间的空间交角很小而丢失重要的模态。因此，在选择6～8 个测点时达到MAC 模态置信准则的理论的要求。

2)从传感器位置优化结果可以看出，测点1～6，9，10 出现次数较多，其中测点1，6 在输入轴侧，说明输入轴所含信息较多可为首选的测试点，但测点6 由于处于连接装置的输入端，信号包含数据量大。在中间轴测点2，5 的信息量与典型故障设置的位置有关，因此这2 测点可作为浮动测点。测点4，3 因为位于输出轴侧，处于传动的末端，故障信息衰减多，测点9，10 位于输出轴侧箱盖边缘处，对箱体的变形信息敏感，可将其作为备选测点因此，综合考虑MAC 非对角元素值和各测点位置对信号的敏感程度，最优测点数为6、7、8，考虑到对称性和经济性，选择6 个传感器的优化位置为［1 2 3 4 5 6］.

表4 CPSO 算法传感器测点布置Tab.4 Test points'layout based on CPSO

PSO 算法和齿轮箱有限元计算相结合，既具有PSO 算法的自适应、全局搜索能力，对目标函数没有特别要求，无需梯度信息等优良特性，还具有有限元软件参数化建模、模态分析容易实现等优点。理论优化结果表明:基于CPSO 的测试点优化布置可以减少无效测试点的数量。

3 齿轮箱箱体试验模态分析

3.1 试验模态分析

试验模态分析是对2.2 节所述的有限元理论建模和模态计算的验证。试验模态分析过程中，对上箱体的一个固定点施加激振力，同时测出其响应，对拾振点所测的响应信号分别作模态分析，得出箱体试验模态的各阶模态参数。表5为10 阶试验模态的固有频率和振型。图6为其中第1 阶振型图，第1 阶频率为42.403 Hz，大体沿轴向(y 方向)摆动，通过对比有限元理论模态的计算结果和振型可知，理论分析结果与模态试验结果振型基本一致，振动频率接近，证明了本文研究中齿轮箱体理论振动模态方法和数据的有效性。

3.2 测点频响特性分析

用信号分析设备求出激振点与响应点之间的传递函数，选取上箱体的10 个主要测点进行分析，为了与2.5 节粒子群优化的理论分析结果进行比较，10 个测点位置如图4所示。测点的x，y，z 三个方向的传递函数出现峰值处的频率和最大幅值，如表6所示。根据振动分析的理论，传感器布置的测点位置应尽量在频响函数峰值响应大，且频率远离齿轮和轴承的特征频率之处，且避开齿轮箱的固有频率。以频响函数分析表6为依据，在正常工况下，对上箱体10 个典型布点为对象进行分析。

表5 齿轮箱试验模态参数及振型Tab.5 Test modal parameters and modal vibration type of gearbox

图6 齿轮箱试验模态的第1 阶振型Fig.6 First vibration type in test modal of gearbox

当对箱体施加激励时，测点1、6 在x 向和z 向的频率响应的振幅的最大峰值总体上都较其它点高。测点2、3 在3 个方向的频率响应的振幅峰值不突出，大小与激励点位置有关。测点4 在y 向，测点5 在y 向和z 向频率响应的振幅的最大峰值总体上都较其它点都高。总体上，这6 个测点的峰值响应频率良好，远离齿轮和轴承特征频率。

测点7、8、9、10 均处与上箱体边缘处，峰值响应频率在中频段较多，幅值大小与激励点位置有关，但频率响应的的最大幅值总体上看，测点7、8 在x 向、z 向响应较y 向强烈，测点9，10 在y 向、z 向较x 向强烈。因此从10 个测点的频响特性分析，测点在x、y、z 三个方向选择排序大体为:x［1 6 7 8 2 3］，y［4 5 2 3 9 10］，z［1 6 5 2 3 7］.综合3 个方向的响应效果，响应强烈前6 位排序为［1 6 5 2 3 7］，其中前5 个测点的位置与粒子群优化结果一致。

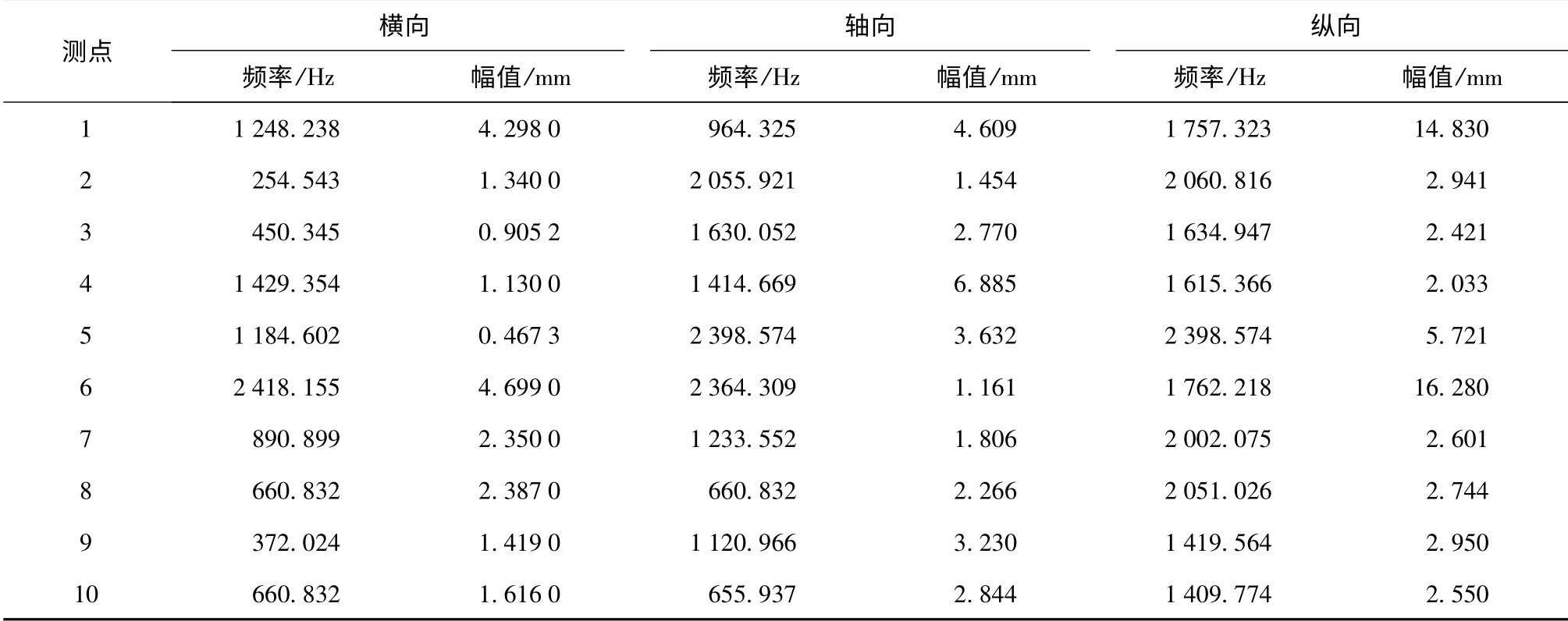
表6 齿轮箱正常工况下频响函数特性分析Tab.6 Frequency response of gearbox in normal condition

在进行齿轮箱模拟故障诊断实验中，利用优化结果的6 个测点［1 2 3 4 5 6］布设加速度传感器，以齿轮箱故障敏感特征为输入，以正常工况和典型故障为输出，建立了拓扑结构为7-12-6 的3 层BP 神经网络故障诊断系统，进行了齿轮箱故障诊断，使故障诊断的精度提高26.1%［8］.

4 结论

提出了基于粒子群优化的齿轮箱传感器优化布置方法，解决多测点传感器的布置和定位问题。根据齿轮箱有限元的模态计算结果，建立了基于模态置信准则的适应度，用粒子群优化算法寻求满足适应度需求的传感器布置方案，包括传感器的数量和测点位置。并进行了齿轮箱模态试验，从试验模态的分析和频响特性分析的结果看，基于粒子群优化方法得到的齿轮箱测点优化的理论结果和试验模态结果基本一致。该方法在复杂结构状态检测和故障诊断中起到理论上指导测试点优化布置的作用。

References)

［1］Cherng An-pan.Optimal sensor placement for modal parameter identification using signal subspace correlation techniques［J］.Mechanical Systems and Signal Processing，2003，17(2):36 -378.

［2］Papadimitriou C.Optimal sensor placement methodology for parametric identification of structural systems［J］.Journal of Sound and Vibration，2004，278:923 -947.

［3］许强.模态测试中传感器优化布设的初步研究［D］.重庆:重庆交通大学，2007.XU Qiang.Preliminary research of optimal sensor placement algorithms for model measurement［D］.Chongqing: Journal of Chongqing Jiaotong University，2007.(in Chinese)

［4］Mani Bhushan，Raghunathan Rengaswamy.Design of sensor location based on various fault diagnostic observability and reliability criteria［J］.Computers and Chemical Engineering，2000，24:735-741.

［5］Burrows K，Burrows A P.Optimal sensor placement for fault detection［J］.Engineering Structures，2001，23:885 -901.

［6］Wang H Q，Song Z H，Wang H.Statistical process monitoring using improved PCA with optimized sensor locations［J］.Journal of Process Control，2002，12:735 -744.

［7］Liu W，Gao W C，Sun Y，et al.Optimal sensor placement for spatial lattice structure based on genetic algorithms［J］.Joural of Sound and Viberation，2008，317(5):175 -189.

［8］魏秀业.基于粒子群优化的齿轮箱智能故障诊断研究［D］.太原:中北大学，2009.WEI Xiu-ye.Study on intelligent fault diagnosis of gearbox based on particle swarm optimization［D］.Taiyuan:North University of China，2009.(in Chinese)

［9］Thomas G C，Clark R D.A modal test design strategy for modal correlation［C］∥Proceedings of the 13th International Modal Analysis Conference1，New York:Union College，Schenectady，1995:927 -933.