基于三角网格模型的平面度在线检测系统的开发

王如官

（天津工业大学，天津 300160）

在线检测利用数控机床的控制系统控制测头测量工件，获取工件表面上测点的坐标信息，通过通信设备把信息传输到计算机上进行数据处理，得出工件的加工余量、加工误差和尺寸公差等。

现代化生产对互换性的要求越来越高[1]，平面度误差，是机械零件及其互换性的重要指标之一，往往是产品质量好坏的关键，在评定机械零件产品质量优劣中起着重要作用。较之其他的规则特征，平面度在线检测功能的实现是比较复杂的，通过对检测过程中遇到问题的探讨，也可以做为实现其他规则特征在线检测的参考。

1 基于三角网格模型的测点分布

1.1 三角网格模型的特点

最常用的三角网格模型描述方式，是STL文件格式。STL文件由3DSystems公司提出并加以广泛推广应用。它使用三角形面片来表示三维实体模型，现己成为CAD/CAM系统接口文件格式的工业标准之一，绝大多数的CAD软件都能生成此种格式文件。这种模型的数据结构简单，能减轻开发软件系统的工作量。它包含的点的三维坐标信息和三角片的法矢信息能满足在线检测数据基本要求。STL文件的ASCII格式如图1所示。STL文件格式包含每个三角片的3个顶点坐标信息和面的法矢信息，三角片的法矢方向遵循右手法则（如图2所示）。

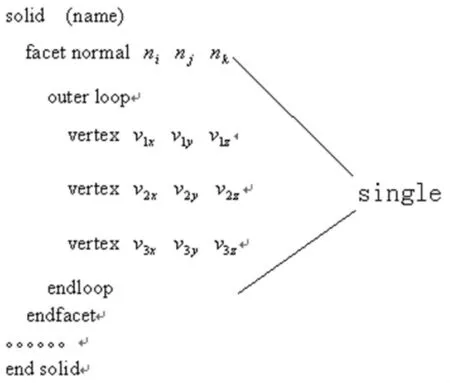
图1 STL文件内数据结构

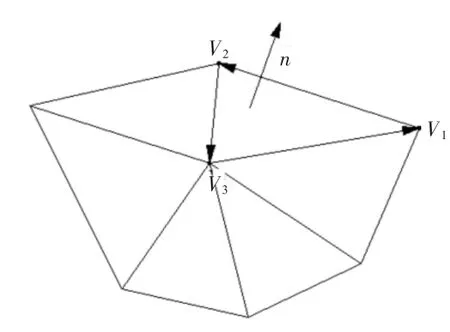
图2 三角片的描述

1.2 测点的分布

具有平面部分的三角网格模型（如图3所示），其三角片的顶点均分布于平面的边缘，而该平面非边缘的区域，则无任何顶点，所以只能通过间接方法去获取，下面介绍一种获取的方法（如图4所示）。点A、B、C分别是三角面片的3个顶点，先把这三角片缩小，变成以点a、点b、点c为顶点的三角型，然后以点a为起始点，b点作为最远的点，朝ab方向，随机地搜索一个点n，最后以n点为起始点，c点为作为最远的点，朝nc方向，随机地搜索一个点p，该点p就是要产生的测点。

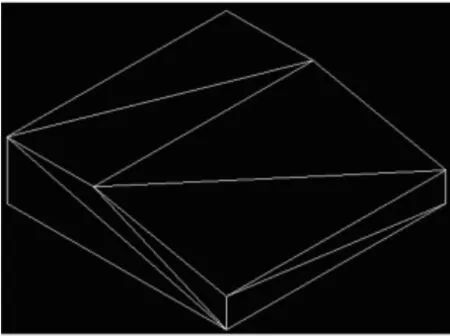
图3 三角网格模型

图4 在三角片内获取测量点的原理图

针对平面度的在线检测，测量点的分布最好是要反映出工件的几何形状和零件的加工方式。图5和图6中点的布置，都反映了其测量要素的平面几何形状。

图5 长方形平面上的测点分布

图6 圆形平面上的测点分布

另一方面，在测量点合理分布的前提下，测点数越多，测量结果受偶然因素的影响也越小。因此在高精度测量时，要适当地增加测量点数。结合精度和效率两方面的因素，一种理想的方法，就是使测点分布的疏密可以刚好包含或接近基本几何形体的特征点，从而较好地反映待测曲面的几何形状信息，实现测点的合理分布。

2 平面度在线检测路径的设计

2.1 测头近距离接近平面的方向

在检测路径的设计中，需考虑测头近距离接近测点时的方向。它决定了应该选择何种测头半径补偿的方法，这对检测精度有很大的影响。测头接触测点的方向有两种：

一种为沿着轴线方向接触零件表面；

另外一种为沿着测点沿法线方向接触零件表面。

第一种方法的缺点是测头在接触测点时，容易产生打滑，产生的测量误差会比较大，并且半径补偿的方法比较复杂；

第二种方法拟补了第一种方法存在的不足，使测头在测量时不但不容易打滑，而且半径补偿是沿着测点的法矢方向补偿一个测头的半径值。因此本文选用第二种方法，处理测头接近测点时的方向问题。

2.2 检测步骤的设计

为了提高在检测每个测点的效率和检测过程的安全性，需要对其检测的步骤进行设计，具体步骤如下。

（1）Step1：测头从开始点出发，接近第一个测点；

（2）Step2：当测头接近测点的时候，为了防止突发的意外造成对测头的损害，测头的运动速度需要被降低；

（3）Step3：当测头非常接近测点的时候，测头以一个比较低的速度运动；

（4）Step4：测头接触测点后，回退；

（5）Step5：完成一个测点的检测后，测头运动到下一个测点的起点，继续进行检测工作。

3 平面度误差的计算

平面度的数据处理，通常采用的方法有对角线法、三点法、综合旋转法、最小二乘法和最小条件法，本文采用最小二乘法。在空间直角坐标系中的平面方程为

在式中a，b，c代表平面法向量的向量数，我们可以以CAD模型中平面的法失暂时代替，其中最大方向的向量数我们令其为1，通过这种算法拟合的平面精度比较高，即上式可以转化成以下公式：

当x的方向数最大时：

当y的方向数最大时：

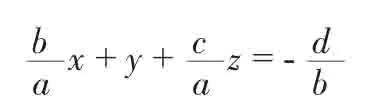
当z的方向数最大时：

以x方向数最大所列式为例，下面具体阐述最小二乘拟合方法。

方程转化为

根据点到平面的距离公式，求出测量点到拟合平面的距离

其中（xi，yi，zi）为测量点坐标。εi为第 i个测量点到拟合平面的距离。n为测量点的个数。利用最小二乘原则，我们求为简化运算，令

用求最小值公式

列出线性方程组，通过列出的方程组可求出最佳的拟合平面方程，而平面度就是平面两侧的测量点到该平面距离最大的差值。

4 实验验证

基于VC++6.0平台，运用上述所提出的基于三角网格模型的测点分布、在线检测路径的设计、平面度误差的计算方法，开发了一个基于三角网格的平面度在线检测系统。在实验验证中，所采用的机床是VMC750立式加工中心，采用FANUC 0i-M系统[2]，定位精度可达0.005 mm。检测所采用的测头，是哈尔滨先锋机电技术开发公司生产的触发式有线通讯测头TP6L。

实验验证所采用的零件CAD模型如图7所示，被检测的对象是该模型中的斜面部分，零件加工出来后，对该斜面的斜面部分进行检测，测点为10个，分析其测点的误差情况（如图8所示），检测的测点误差在0.015～0.030 mm之间。可见，实验检测出来的测点的误差相当低，可以进行后继的平面度误差的分析。对该零件的斜面另外进行10次检测，每次以随机的方式在该斜面上产生待检测的20个测点，每次检测完后记录下平面度误差，列出表1。平面度误差最小为0.022 5 mm，最大为0.028 6 mm，该精度很高。通过以上实验，验证了该平面度在线检测方法的可行性。

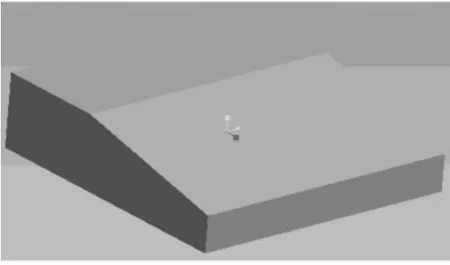
图7 实验的CAD模型

图8 在线检测测点的误差分析（单位：mm）

表1 平面度误差的分析 单位：mm

5 结束语

文章针对平面度的在线检测，提出一种基于三角网格模型的检测方法。对该研究所涉及到的平面的测点分布、检测路径的设计、平面度误差的计算等关键问题，进行了研究，为检测系统的研发提供了技术支持。最后基于VC++6.0平台，开发了一个基于三角网格的平面度在线检测系统，并且对平面度的在线检测理论进行了实验验证。实验结果得出，平面度的检测误差最小为0.022 5 mm，最大为0.028 6 mm，该精度相当高，验证了该平面度在线检测方法的可行性。

[1]李 柱.互换性与测量技术基础[M].北京：计量出版社，1984.

[2]费业泰.误差理论与数据处理[M].北京：机械工业出版社，1985.

[3]史文彬.关于使用数控机床实现在线测量——系统连接的探索与研究[D].太原:中北大学，2007.

[4]E.Mession，T.R.Kramer HH，F.M.Proctor，H.Scott.A feature-based inspection and machining system[J].Computer-Aided Design，2001，（33）：653-669.

[5]马云辉.陶崇德.数控机床用在线检测系统的研究[J].组合机床与自动化加工技术，1990，(8)：45-47.

[6]刘利剑.加工中心在线测量功能的实现[J].机械工程师，2002，(12)：501-504.

[7]刘丽冰，桑宏强，陈英姝.用于加工中心的在线检测新方法研究[J].新技术新工艺，2005，(11)：16-18.

[8]孙志海.基于CAD的加工中心在线检测系统研究与开发[D].天津:河北工业大学，2003.

[9]辛 娜.加工中心在线检测实物编程技术研究及系统开发[D].天津：河北工业大学，2003.

[10]王广彦.基于CAD的加工中心在线检测关键技术研究[D].天津：河北工业大学，2002.

[11]花国梁.精密测量技术[M].北京：清华大学出版社，1986.

[12]傅成昌.形位误差检测技术[M].北京：机械工业出版社，1990.