磁流变阻尼器力学性能及减震试验研究

杨孟刚，陈政清

(1. 中南大学 土木建筑学院，湖南 长沙，410075；2. 湖南大学 风工程试验研究中心，湖南 长沙，410082)

磁流变阻尼器力学性能及减震试验研究

杨孟刚1，陈政清2

(1. 中南大学 土木建筑学院，湖南 长沙，410075；2. 湖南大学 风工程试验研究中心，湖南 长沙，410082)

通过RD1097型MR阻尼器的力学性能试验，获得不同频率、不同振幅、不同输入电流下的阻尼力与位移、速度的关系曲线；提出一种改进的MR阻尼器反正切函数非线性模型；采用RD1097型MR阻尼器，进行正弦波和El-Centro波下的MR阻尼器减震试验研究。研究结果表明：提出的阻尼器力学模型具有识别参数少、编程方便、精度较高等特点，不仅能较准确描述低速下阻尼力与速度的关系，而且能模拟摩擦滞后效应，对于固定频率振动和随机地震波下的阻尼力模拟有效；MR阻尼器具有较好的减震效果，在El-Centro波激励下，可使位移峰值及其均方根分别减小62.75%和77.17%。

磁流变阻尼器；阻尼器力学模型；减震试验；力学性能

近年来，磁流变阻尼器(即 MR阻尼器)因其具有能耗少、出力大、响应速度快、结构简单、阻尼力连续顺逆可调等良好的智能阻尼特性，已在斜拉桥拉索振动控制、高耸结构抗风抗震、海洋平台结构减震等方面得到应用[1−4]。MR阻尼器是一种高度非线性系统，建立和寻找1个有效的MR阻尼器模型是其得到工程应用的关键。已有的MR阻尼器参数化模型主要有Bingham黏塑性模型、修正的Bingham模型、非线性双黏性模型、Bouc-Wen模型、现象模型、改进的现象模型、修正的Dahl模型、Sigmoid模型、双Sigmoid模型、双曲正切滞回模型等[5−11]；非参数模型主要包括多项式模型、神经网络模型、模糊逻辑模型等[12−15]。在这些模型中，非参数模型由于缺乏物理概念，需要通过大量的数据训练，适应性较差；参数化模型中有些无法捕获阻尼力与速度的非线性行为或精度不高，而有些模型过于复杂，参数多，不易识别。目前，人们对基于 MR阻尼器开展的减震控制理论的研究较多[16−19]，而对减震试验研究较少，且主要集中在建筑结构方面[20−22]。在此，本文作者结合减震试验需要，对RD1097型MR阻尼器进行力学性能进行测试，提出参数少、控制应用方便的阻尼器力学模型，并进一步开展MR阻尼器减震试验研究，验证阻尼器模型的有效性和减震效果。

1 RD1097型 MR阻尼器力学性能测试

RD1097型MR阻尼器是Load公司生产的小吨位摩擦型阻尼器，该阻尼器最大出力为100 N，最大输入电流为 0.5 A，最大行程为−25～25 mm。为了获得RD1097型MR阻尼器的力学性能，试验采用的频率分别为 0.5，1.0，1.5，2.0，2.5，3.0，3.5 和 4.0 Hz，振幅分别为2.5，5.0，7.5和10.0 mm，输入电流分别为 0，0.05，0.10，0.15，0.20，0.25，0.30，0.35，0.40和 0.45 A。部分测试结果如图 1～3所示。由图 1～3可知：

(1) 阻尼器的最大阻尼力随电流增加而递增，当电流达到一定值后，最大阻尼力达到饱和；

(2) 阻尼器的最大阻尼力随频率增加而递增，随振幅增大而略增大；

(3) 在频率为2 Hz、振幅为10 mm，电流分别为0.2 A和0 A时，阻尼器的最大阻尼力之比约为3，说明阻尼力的可调性较好；

(4) 阻尼器的阻尼特性表现为非线性滞回特性，位移滞回曲线为丰满的矩形，说明该阻尼器的耗能性能很好；

(5) 阻尼器存在摩擦滞后效应，它的速度滞回曲线由3个滞回环组成，中央较大的为主滞回环，两端较小的为次滞回环。

2 MR阻尼器力学模型

根据RD1097型MR阻尼器的力学性能试验测试结果，提出一种改进的反正切函数非线性模型，该模型的阻尼力表示为

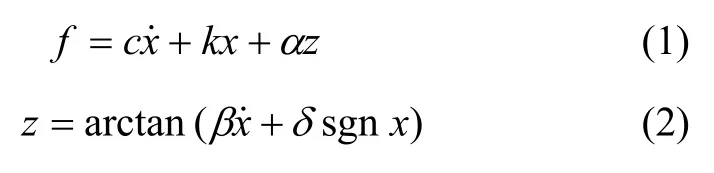
图1 不同电流下阻尼器力学性能曲线(位移幅值为10 mm，频率为2 Hz)Fig.1 Mechanical behavior of MR damper under different currents when amplitude is 10 mm and frequency is 2 Hz

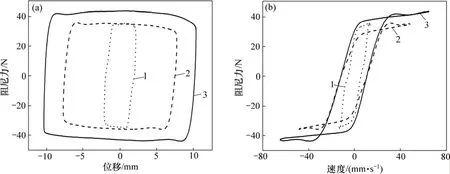
图2 不同位移幅值下阻尼器力学性能曲线(频率为1 Hz，电流为0.4 A)Fig.2 Mechanical behavior of MR damper under different amplitudes when frequency is 1 Hz and current is 0.4 A

图3 不同频率下阻尼器力学性能曲线(位移幅值为10 mm，电流为0.2 A)Fig.3 Mechanical behavior of MR damper under different frequencies when amplitude is 10 mm and current is 0.2 A

式中：c为黏滞阻尼系数；k为蓄能器刚度；x为阻尼器活塞位移(mm)；x为阻尼器活塞速度(mm/s)；变量z描述了阻尼力关于速度的滞回量，代表库仑阻尼力；均为待定参数，分别决定滞回环的高度、倾斜度和宽度。采用遗传算法，编制了Matlab程序，分别对不同频率、不同振幅、不同电流下的试验结果进行模型参数识别，然后对各参数进行回归拟合，得到RD1097型MR阻尼器改进的反正切函数非线性模型参数表达式为：

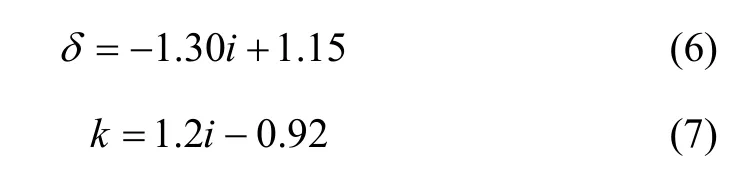
式中：i为阻尼器输入电流(A)。

根据识别参数值，将由式(1)获得的模型结果与试验结果进行对比，结果如图4所示。由图4可知：改进的反正切函数非线性模型的阻尼力与位移、速度曲线和试验曲线拟合较好，不仅克服了Bingham模型低速模拟不精确及相对速度方向发生变化时阻尼力不平滑过渡的不足，而且能够模拟摩擦滞后效应，对于不同振幅和不同频率具有较好的通用性，充分说明该模型是有效的。由于识别参数较少，编程方便，可较好地应用于工程振动控制。

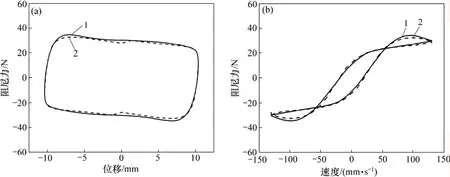
图4 试验与模型曲线对比(位移幅值为10 mm，频率为2 Hz，电流为0.2 A)Fig.4 Comparison between experimental and analyzed responses when amplitude is 10 mm, frequency is 2 Hz and current is 0.2 A

3 MR阻尼器减震试验

3.1 试验装置

为了验证提出的MR阻尼器力学模型的有效性以及MR阻尼器的减震效果，设计制作了如图5所示的试验装置。通过配重、安装测试后的试验装置参数为：质量2 kg，刚度9.235 kN/m，频率0.342 Hz，阻尼比1.52%，1个RD1097型MR阻尼器。减震试验在广州大学工程抗震研究中心完成。

图5 减震试验装置Fig.5 Experimental setup of seismic response reduction

3.2 输入地震波及试验工况

本次试验采用的输入地震波为 El-Centro波和正弦波。采用的 El-Centro波波形如图 6所示(其中，1g=9.8 m/s2)，输入的正弦波函数为 0 .3sin (2πt)。考虑到振动台控制系统由于输入时间间隔过小会造成地震波波形失真的实际情况，选定输入频率为64 Hz，即输入时间间隔为0.015 625 s；同时，为了满足位移计和阻尼器阻尼力的测试范围，在减震试验时，将El-Centro波的幅值缩小至原来的1/8。

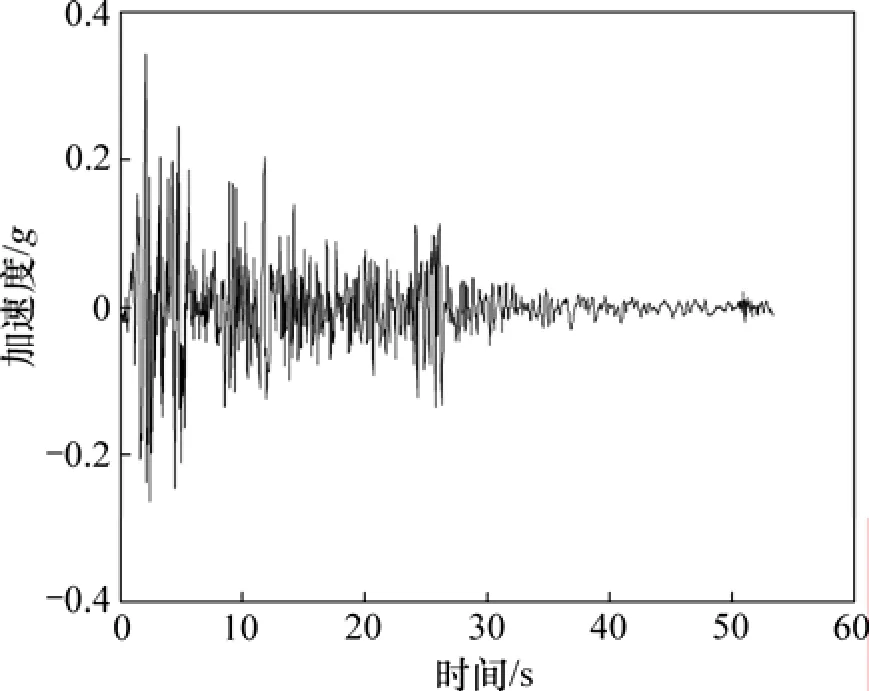
图6 El-Centro地震波Fig.6 El-Centro earthquake wave

试验测试包括无控、被动控制(电流分别为0，0.1，0.2，0.3，0.4和0.5 A)以及半主动Bang-Bang控制等8种工况。其中半主动Bang-Bang控制算法如下：

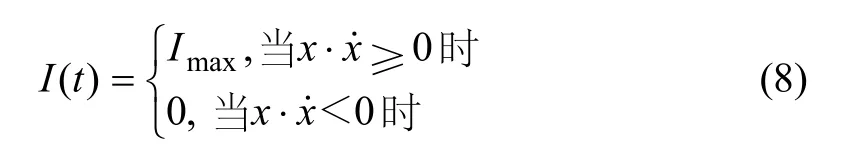
式中：x为MR阻尼器位移；x为MR阻尼器速度；Imax为 RD1097型 MR阻尼器的最大饱和电流，其值为0.5 A。

3.3 减震效果分析

在正弦波和El-Centro波下，被动控制输入电流为0.5 A时的仿真阻尼力与实测阻尼力结果比较如图 7所示，El-Centro波下的各种控制工况位移与无控实测位移比较如图8所示。各种控制工况实测位移反应峰值、均方根值及相应的减震率见表 1。图7～8及表1中仅列出了被动控制(0，0.2和 0.5 A)及半主动Bang-Bang控制的试验结果。减震率 定义如下：

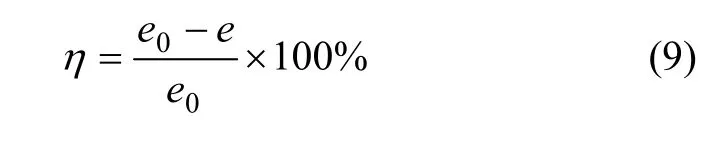
图7 被动控制电流为0.5 A时仿真分析与实测阻尼力比较Fig.7 Comparison between damping forces by analysis and measure under input current of 0.5 A

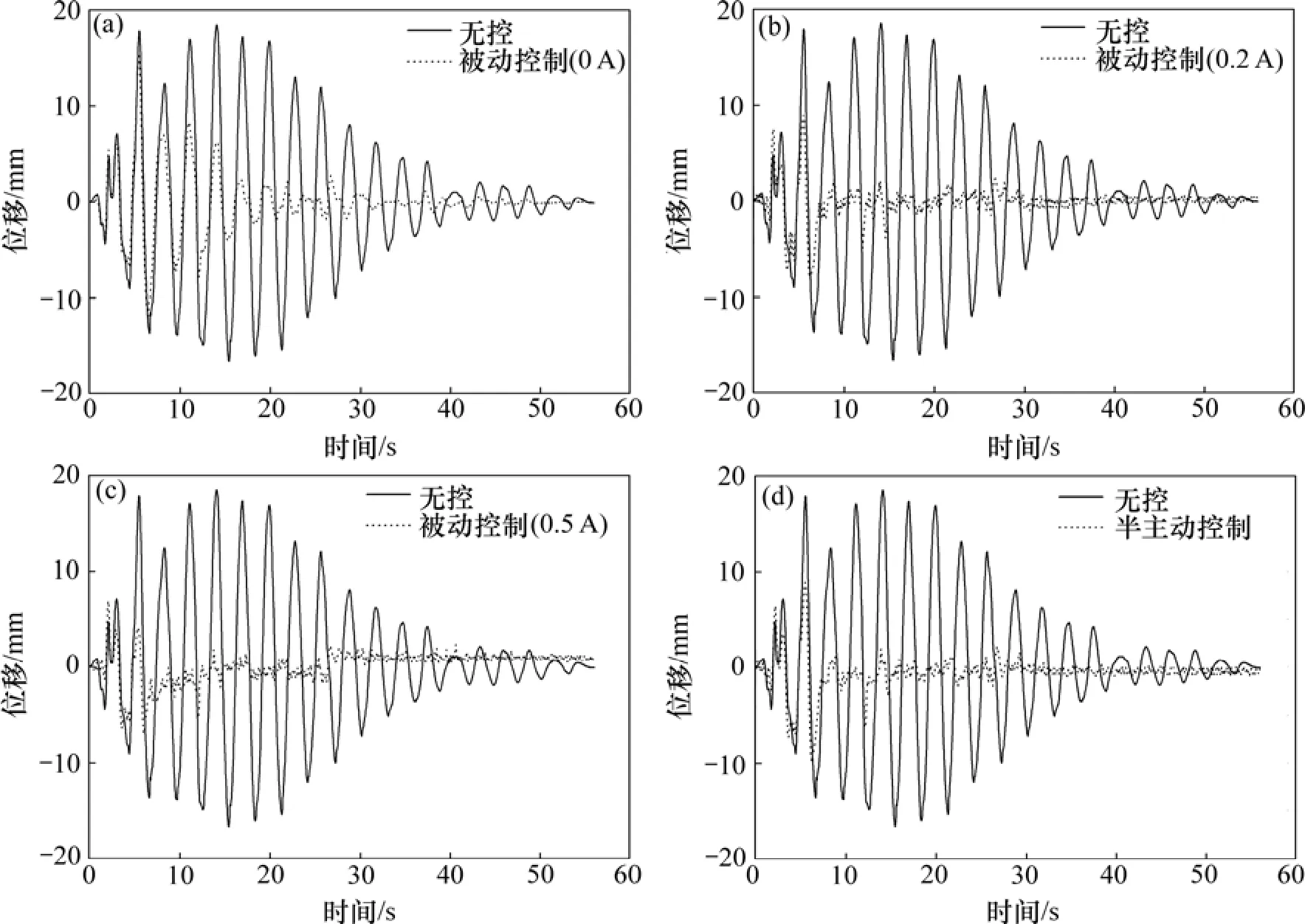
图8 El-Centro波下的实测位移比较(El-Centro波)Fig.8 Comparison between measured displacements under El-Centro wave

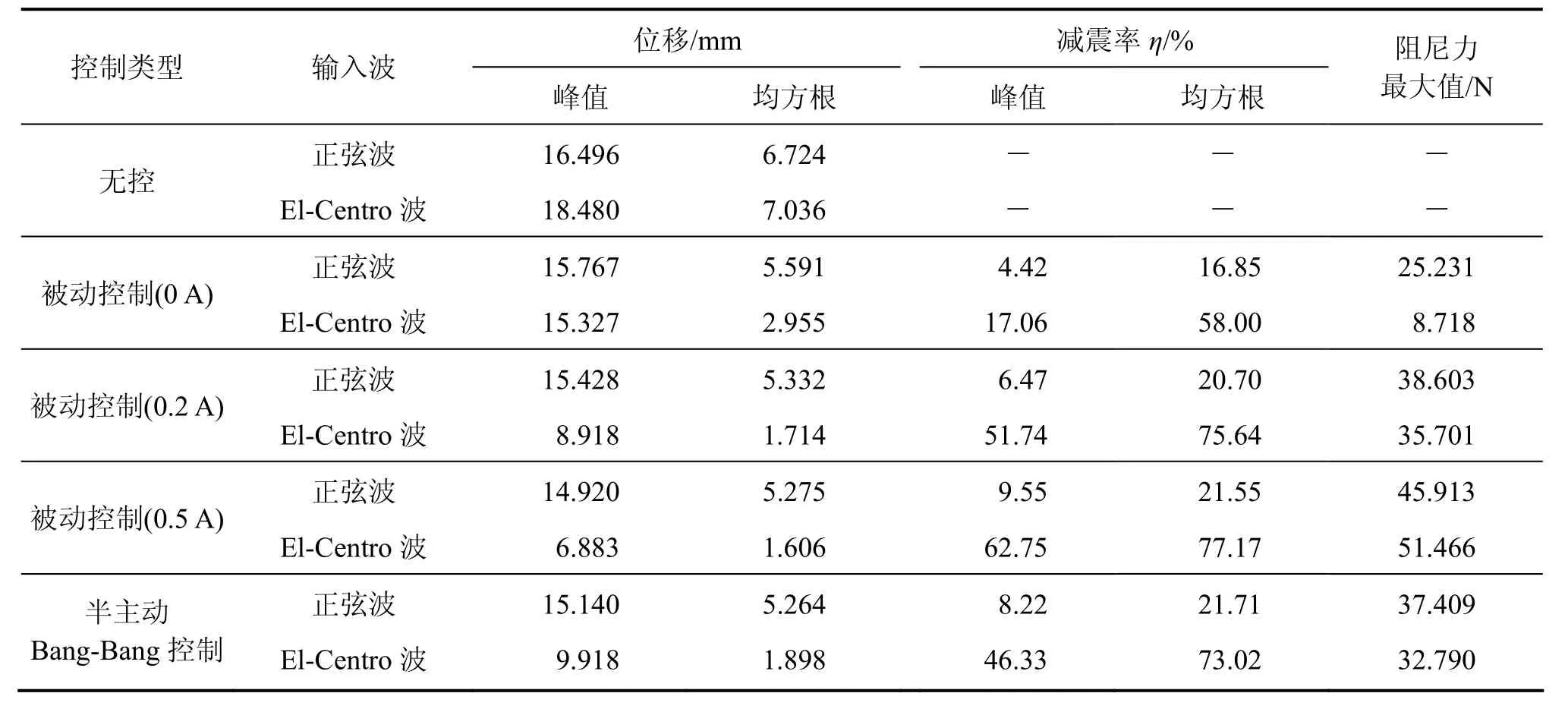
表1 实测位移与阻尼力Table 1 Results of measured displacements and damping forces

其中：e0为无控反应值；e为有控反应值。由图7～8以及表1可以得到：

(1) 仿真分析和实测的 MR阻尼器阻尼力的时程曲线非常接近，说明本文提出的MR阻尼器力学模型对于固定频率振动和随机地震波下的阻尼力模拟是有效的。

(2) 在正弦波被动控制中，起振初期位移峰值减小不明显，但随后减小显著并趋于稳定。这是由于阻尼器在电流较小时就产生了较大的阻尼力。当电流为0.5 A时，位移峰值及其均方根分别减小了 9.55%和21.55%。

(3) 在El-Centro波被动控制中，随着输入电流的增大，位移峰及其均方根逐渐减小，减震效果显著。电流为0.5 A时为最优被动控制，位移峰值及其均方根分别减小了62.75%和77.17%。

(4) 2种输入下的半主动Bang-Bang控制的位移减震效果均比最优被动控制的位移减震效果差，但两者的阻尼力最大值均比最优被动控制的小。

4 结论

(1) 阻尼器的最大阻尼力随电流、频率增加而增加，当电流达到一定值后，最大阻尼力达到饱和；阻尼器具有较好的可调性和耗能性能；该类型阻尼器存在摩擦滞后效应。

(2) 提出了一种改进的 MR阻尼器反正切函数非线性模型，采用遗传算法进行了参数识别。该模型具有较高的精度，且识别参数较少，编程方便，可较好地应用于工程振动控制。

(3) 本文提出的 MR阻尼器力学模型对于固定频率振动和随机地震波下的阻尼力模拟是有效的；MR阻尼器具有较好的减震效果，在El-Centro波激励下，MR阻尼器可使位移峰值及其均方根分别减小62.75%和77.17%。

[1] 欧进萍. 结构振动控制: 主动、半主动和智能控制[M]. 北京:科学出版社, 2003: 340−346.

OU Jin-ping. Structure vibration control: Active, semi-active and smart control[M]. Beijing: Science Press, 2003: 340−346.

[2] 禹见达, 陈政清, 曹宏, 等. 永磁调节式MR阻尼器试验研究及工程应用[J]. 振动工程学报, 2006, 19(4): 532−536.

YU Jian-da, CHEN Zheng-qing, CAO Hong, et al. Experimental study and implementation of the adjustable permanent magnet MR damper[J]. Journal of Vibration Engineering, 2006, 19(4):532−536.

[3] Ha Q P, Kwok N M, Nguyen M T, et al. Mitigation of seismic responses on building structures using MR dampers with Lyapunov-based control[J]. Structural Control and Health Monitoring, 2008, 15(4): 604−621.

[4] 陈波, 郑瑾, 瞿伟廉. 基于磁流变阻尼器的大跨越输电塔线体系风致振动控制[J]. 振动与冲击, 2008, 27(3): 71−75.

CHEN Bo, ZHENG Jin, QU Wei-lian. Wind-induced response mitigation of transmission tower line system by using magnetorheological dampers[J]. Journal of Vibration and Shock,2008, 27(3): 71−75.

[5] Stanway R, Sproston J L, Stevens N G. Non-linear modeling of an electro-rheological vibration damper[J]. Journal of Electrostatics, 1987, 20: 167−184.

[6] Gamota D R, Filisko F E. Dynamic mechanical studies of electrorheological materials: Moderate frequencies[J]. Journal of Rheology, 1991, 35: 399−425.

[7] Spencer Jr B F, Dyke S J, Sain M K, et al. Phenomenological model of a magnetorheological damper[J]. Journal of Engineering Mechanics, ASCE, 1997, 123(3): 230−238.

[8] 周强, 瞿伟廉. 磁流变阻尼器的两种力学模型和试验研究[J].地震工程与工程振动, 2002, 22(4): 144−150.

ZHOU Qiang, QU Wei-lian. Two mechanic models for magnetorheological damper and corresponding test verification[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(4): 144−150.

[9] Yang G, Spencer Jr B F, Dyke S J, et al. Large-scale MR fluid dampers: Modeling and dynamic performance considerations[J].Engineering Structures, 2002, 24: 309−323.

[10] 李秀领, 李宏男. 磁流变阻尼器的双Sigmoid模型及试验验证[J]. 振动工程学报, 2006, 19(2): 168−172.

LI Xiu-ling, LI Hong-nan. Double-sigmoid model for magnetorheological damper and corresponding experiment verification[J]. Journal of Vibration Engineering, 2006, 19(2):168−172.

[11] Kwok N M, Ha Q P, Nguyen T H, et al. A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization[J]. Sensors and Actuators, 2006, 132: 441−451.

[12] Du H P, Kam Y S, James L. Semi-activeH−∞ control of vehicle suspension with magneto-rheological damper[J]. Journal of Sound and Vibration, 2005, 283: 981−996.

[13] Xia P Q. An inverse model of MR damper using optimal network and system identification[J]. Journal of Sound and Vibration,2003, 266: 1009−1023.

[14] 汪小华, 张培强. 磁流变液阻尼器的模糊逻辑非参数建模[J].中国科学技术大学学报, 2000, 30(2): 218−222.

WANG Xiao-hua, ZHANG Pei-qiang. Fuzzy-logical non-parameter modeling of MR damper[J]. Journal of China University of Science and Technology, 2000, 30(2): 218−222.

[15] 王修勇, 宋璨, 陈政清, 等. 磁流变阻尼器的性能试验与神经网络建模[J]. 振动与冲击, 2009, 28(4): 42−46.

WANG Xiu-yong, SONG Can, CHEN Zheng-qing, et al. Test of a MR damper and its modeling using neural network[J]. Journal of Vibration and Shock, 2009, 28(4): 42−46.

[16] 杨孟刚, 陈政清, 胡建华. 自锚式悬索桥磁流变阻尼器减震控制研究[J]. 土木工程学报, 2006, 39(11): 84−89.

YANG Meng-gang, CHEN Zheng-qing, HU Jian-hua. Study on the seismic response control of self-anchored suspension bridges with MR dampers[J]. China Civil Engineering Journal, 2006,39(11): 84−89.

[17] 秦顺全, 瞿伟廉. 天兴洲公铁两用斜拉桥主梁纵向地震、列车制动及行车移动荷载响应的混合控制[J]. 桥梁建设, 2008(4):1−5.

QIN Shun-quan, QU Wei-lian. Hybrid control of longitudinal vibration responses in deck of Tianxingzhou rail-cum-road cable-stayed bridge caused by earthquake, train braking and vehicle moving loads[J]. Bridge Construction, 2008(4):1−5.

[18] 徐晓龙, 孙炳楠. 基于智能算法的高层建筑非线性地震反应的MR阻尼器半主动控制[J]. 工程力学, 2008, 25(1): 209−216.

XU Xiao-long, SUN Bing-nan. Intelligent algorithm based semi-active control of MR damper of nonlinear seismic response[J]. Engineering Mechanics, 2008, 25(1): 209−216.

[19] 李忠献, 林伟, 丁阳. 多维地震激励下空间结构MR阻尼器半主动控制[J]. 天津大学学报, 2007, 40(5): 512−518.

LI Zhong-xian, LIN Wei, DING Yang. Semi-active control on spatial structures using MR damper under multi-dimensional earthquake excitations[J]. Journal of Tianjin University, 2007,40(5): 512−518.

[20] Lee H J, Jung H J, Cho S W, et al. An experimental study of semiactive modal neuro-control scheme using MR damper for building structure[J]. Journal of Intelligent Material Systems and Structures, 2008, 19(9): 1005−1015.

[21] 杜成斌, 石平才, 于国军, 等. 带有磁流变阻尼器的结构振动实时控制试验[J]. 河海大学学报: 自然科学版, 2009, 37(3):308−312.

DU Cheng-bin, SHI Ping-cai, YU Guo-jun, et al. Real-time vibration control of frame structures with magneto-rheological dampers[J]. Journal of Hohai University: Natural Sciences, 2009,37(3): 308−312.

[22] Zapateiro M, Karimi H R, Luo N. Real-time hybrid testing of semiactive control strategies for vibration reduction in a structure with MR damper[J]. Structural Control and Health Monitoring,2010, 17(4): 427−451.

(编辑 陈灿华)

Experimental research on mechanical behavior and seismic response reduction of MR damper

YANG Meng-gang1, CHEN Zheng-qing2

(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;2. Wind Engineering Research Center, Hunan University, Changsha 410082, China)

The force-displacement and force-velocity curves of MR damper at different frequencies, amplitudes and input currents were obtained by the mechanical behavior test of RD1097 type MR damper. Furthermore, an improved arc tangent function nonlinear model of MR damper was put forward, and the seismic response reduction test of the above type MR damper under the sine wave and El-Centro wave was implemented. The results show that the improved MR damper mechanical model has the characteristics of less identifiable parameters, programming conveniently and high precision, and it can not only describe the relationship between the damping force and displacement precisely, but also simulate frictional lagging effect well. It is very effective for the model to simulate the damping force during invariant frequency vibration and random seismic waves. The structure response with MR damper can be evidently controlled.With the excitation of the El-Centro wave, the peak and its average square root of the displacement response with MR damper decrease by 62.75% and 77.17%, respectively.

magnetorheological damper; damper mechanical model; seismic response reduction test; mechanical behavior

TU352.1

A

1672−7207(2010)06−2327−07

2010−04−22；

2010−07−02

国家自然科学基金资助项目(50908231)

杨孟刚(1976−)，男，江西安义人，博士，副教授，从事桥梁抗震与非线性研究；电话：0731-82656820；E-mail: mgyang@mail.csu.edu.cn