基于多尺度MSR法的边坡体系可靠度分析

谢桂华，张家生，刘荣桂，李继祥

(1. 江苏大学 理学院，江苏 镇江，212013；2. 中南大学 土木建筑学院，湖南 长沙，410075；3. 武汉工业学院 土木系，湖北 武汉，430023)

基于多尺度MSR法的边坡体系可靠度分析

谢桂华1,2，张家生2，刘荣桂1，李继祥3

(1. 江苏大学 理学院，江苏 镇江，212013；2. 中南大学 土木建筑学院，湖南 长沙，410075；3. 武汉工业学院 土木系，湖北 武汉，430023)

为解决常规的体系可靠度方法难以计算具有众多失效模式的复杂边坡稳定可靠度的问题，研究基于矩阵的体系可靠度法(MSR法)分析边坡体系的方法；结合多尺度法，把边坡体系拆分为多个并行子体系，每个并行子体系作为体系的一个“超构件”，以达到减少优化变量个数、降低系数矩阵规模的目的。对矿山边坡体系进行实例分析。研究结果表明：MSR法能获得比常规界限法更加精确的计算结果；将MSR法与多尺度法相结合，可解决失效模式较多的复杂边坡体系可靠度的计算问题，扩大MSR法的应用体系范围；MSR法使边坡的体系失效概率估计区间稍增大，但计算量呈指数级减少，且可利用现有优化软件进行矩阵运算和优化计算，便于实现边坡稳定性的评估工作。

复杂边坡；体系可靠度；MSR法；多尺度

近年来，决策、风险评估和风险管理成为岩土工作者新的研究热点[1−2]，其中，边坡失效风险的量化是灾害评估的前提和重要内容。目前，边坡稳定性问题中存在显著的不确定性这一观点已经成为众多研究者的共识，关于边坡可靠性问题的研究亦取得了丰硕的成果[3−6]。然而，上述成果主要是针对单一失效模式的边坡可靠性问题。事实上，边坡可能发生不同模式的破坏，每一模式又可能具有多个甚至无限个潜在滑面，故其可靠性问题更适合采用体系可靠度方法来分析。另一方面，由于体系可靠度计算及边坡稳定性问题本身的复杂性，迄今，关于边坡体系可靠度的研究成果仍很少[7−11]。上述研究成果中，除文献[9]外，计算方法均采用Ditlevsen的窄界限公式。窄界限公式只能考虑2个失效模式的相关性，应用时要求所有体系构件的单一失效概率和两两联合失效概率信息必须全部已知，且仅限于失效模式较少、失效概率不大的串联体系，计算过程较复杂，尤其是在复杂边坡中很难应用。文献[9]采用矩阵计算，通过线性规划(LP法)分析岩质边坡的体系失效概率，克服了以上缺点，但由于该法的优化变量随着体系构件数增加而呈指数级增长，且在应用中需要借助计算软件完成优化过程，故所分析体系的构件数将受到应用软件对计算量的要求和对计算机内存的限制；同时，当构件较多时，该法中构件向量很难识别。鉴于以上原因，该法仍难以应用于构件较多的复杂体系中。本文作者针对上述方法的不足，进一步研究采用基于矩阵的体系可靠度计算方法，通过计算机自动识别体系的构件向量，探讨将多尺度法与 MSR法结合运用，以解决复杂边坡体系可靠度计算中出现的问题。

1 基于矩阵的体系可靠度(MSR)法

1.1 MSR法的基本原理[12]

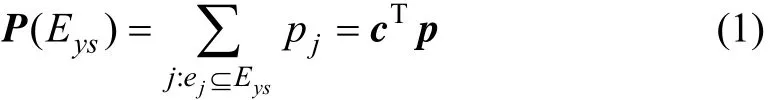
式中：c为MECE事件概率的系数向量，其中的元素表示体系事件发生时，对应MECE事件的状态；p为MECE事件的概率向量，可用下式计算：

其中：“.*”为MATLAB中矩阵元素之间进行乘操作的操作符。采用式(3)和(4)可以方便地获得任意体系事件向量Esys。

根据以上原理，在边坡体系可靠度问题中，结构体系和结构构件包含2个事件：失效事件和可靠事件，即si＝2(i＝1, 2, …,n)。故由n个构件组成体系的样本空间可分为2n个MECE事件，从而可应用式(1)计算体系失效概率。

1.2 识别构件事件向量

当构件不多时，可根据图例直接识别事件向量c[12]，但对于复杂体系，如构件数目n＞5的体系，难以直接识别。为此，本文采用如下递推公式，通过计算机程序构造体系构件的事件向量c：

1.3 构件统计相关的体系失效概率计算

当构件统计相关时，不能采用式(1)计算体系的失效概率。Song等[13]提出采用条件概率来确定P。然而，由于边坡各失效模式之间的相关性与很多因素有关，条件概率很难确定，故该法并不适合边坡体系的可靠性计算。为此，根据各失效模式的相关信息，采用线性规划(LP法)[14]获得体系事件概率的优化边界。

线性规划即对线性函数在规定约束条件下求最小(最大)值，其数学表达式为

通过 MSR法得到的体系概率区间是在任意给定信息下能获得的最窄区间，这已被 Bertsimas等[15]所证明。

2 多尺度方法

应用 MSR法时，向量和矩阵随着构件数的增加和约束条件强化呈指数级增长，因此，对于具有很多失效模式的边坡体系而言，其分析过程对计算机内存容量和软件运算能力的要求也会相应提高，从而限制了 MSR法的应用。为此，本文结合多尺度法[16]，研究MSR在复杂边坡中的应用方法。

多尺度法将大型体系拆分为多个小型问题，先并行计算小型子体系的概率，再在此基础上合并为综合体系来求得整个体系的概率。主要方法如下：选择体系中的某些构件作为一个子体系，称之为“超构件”，以[i](i=1，2，3，…)表示，其中i为“超构件”的编号。“超构件”在整个体系中被看做一个体系构件。显然，如果体系中有n个构件，1个“超构件”[1]，且“超构件”中含有k个体系构件，则该体系的等效构件数相应为n−k+1个，即体系构件数目减少了k−1，从而应用MSR法计算体系时，矩阵的行、列数从2n变为 2n−k+1，减少了 2k−1。同样地，引入“超构件”[2]，[3]，…，则整个体系的计算规模可以进一步降低，直到矩阵规模满足计算要求为止。

对于某些大型体系，仅采用“超构件”来拆分体系是不够的，此时，可借助“超构件”的概念，将多个“超构件”构成“超超构件”，“超超超构件”等，直到满足算法对矩阵和向量的要求。

3 工程应用

某铜矿经多年露天开采，形成了北西向展布的筒状矿体。露采范围顶部最大标高518 m，封闭标高110 m，终了最低标高为−220 m，面积约4 km2。剥采由南东向北西推进，形成多处人工高边坡。本文主要研究东南区边坡1、边坡2、边坡3、边坡4组成的矿山边坡体系的稳定性。

经研究，初步确定该矿山体系中各地段潜在的破坏模式如表1所示，矿区边坡体系简图如图1所示。其中：1，2，3，4分别代表上述4个边坡，gi(i=1，2，…)代表失效模式，即体系构件，每个构件的物理意义如表1所述。

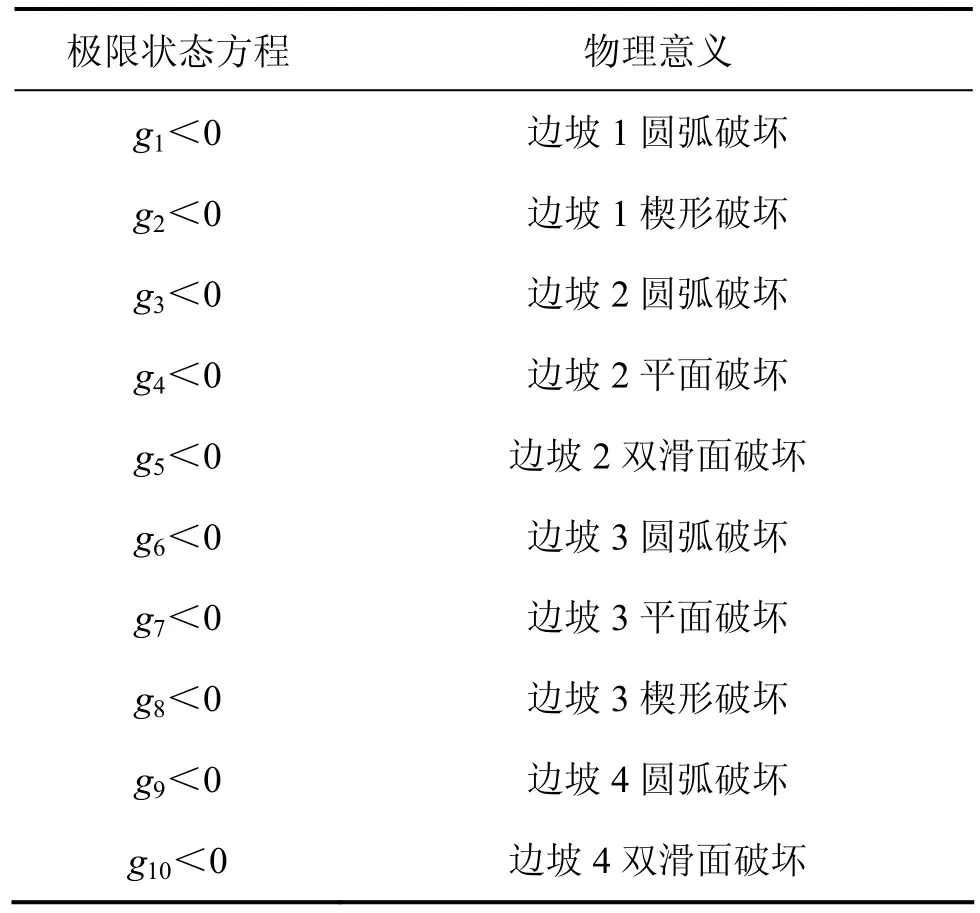
表1 体系构件功能函数及对应的物理意义Table 1 Physical meaning of performance functions for system components

经进一步分析可知，图1中阴影部分标出的构件均含有多个关键滑面：g3存在3个关键圆弧滑面，g5含4个不同双滑面破坏，g8由3组节理形成3个楔形破坏模式，g9含2个圆弧破坏模式。故整个矿山边坡体系中共涉及18个关键滑面，存在18种潜在破坏模式，每一种破坏模式可视为1个体系构件，且子体系边坡1、边坡2、边坡3、边坡4和矿山边坡体系的构件数分别为2，8，5，3和18，4个边坡和整个矿区体系的样本空间分别被分为4，256，32，8和262 144个MECE事件。

为了得到矿山体系的失效概率，考虑到整个体系的优化变量多达218，仅采用MSR法时计算量将超出常见优化软件能处理的范围，故引入多尺度法以减少矩阵的规模。将g3，g5，g8和g9作为“超构件”，则边坡相应地成为“超构件”或“超超构件”(如图1中虚线框出的部分)。各边坡在疏干、饱水2种状态下的体系失效概率估计区间见表 2，为比较本文方法与常规的宽界限法、窄界限法的优劣，将界限估计法的分析结果，同列于表2中。整个矿山边坡体系在疏干状态下的失效概率区间Pf=[0.259 76, 0.267 45]，对应可靠指标β=[0.384 9, 0.385 7]；若全部边坡均处于饱水状态，则Pf=[0.802 87, 0.869 49]。

为进一步比较各种方法所得结果的精确性，并考察相关性对“超构件”和体系失效概率的影响，假设超构件中内部构件的相关系数ρ在[0, 1]内变化，采用MSR法计算各“超构件”在疏干状态下的失效概率曲线如图2所示。结合多尺度法，计算“超构件”边坡1、边坡3、边坡4以及“超超构件”边坡2在疏干状态下的体系失效概率变化曲线如图3所示。

为说明多尺度MSR法的优劣，将失效模式g3，g5和g8作为“超构件”，采用多尺度法计算边坡2与边坡3的体系失效概率，各种处理方法得出的结果如图4所示。

图4(a)中：“MSR法1”为将边坡2的3个圆弧破坏(g3)和4个双滑面破坏(g5)作为2个超构件时的计算结果；“MSR法 2”为将其 3个圆弧破坏模式作为 1个“超构件”时的结果；“MSR法3”为将4个双滑面破坏模式作为1个超构件时的结果；“MSR法4”为不引入超构件时的结果。图4(b)中：“MSR法5”为将边坡3的3个圆弧破坏模式作为“超构件”时的计算结果；“MSR法6”为不引入超构件时的结果。

图1 矿山边坡体系计算简图Fig.1 Calculation sketch of slope system

表2 边坡子体系的失效概率Table 2 Failure probabilities of slopes

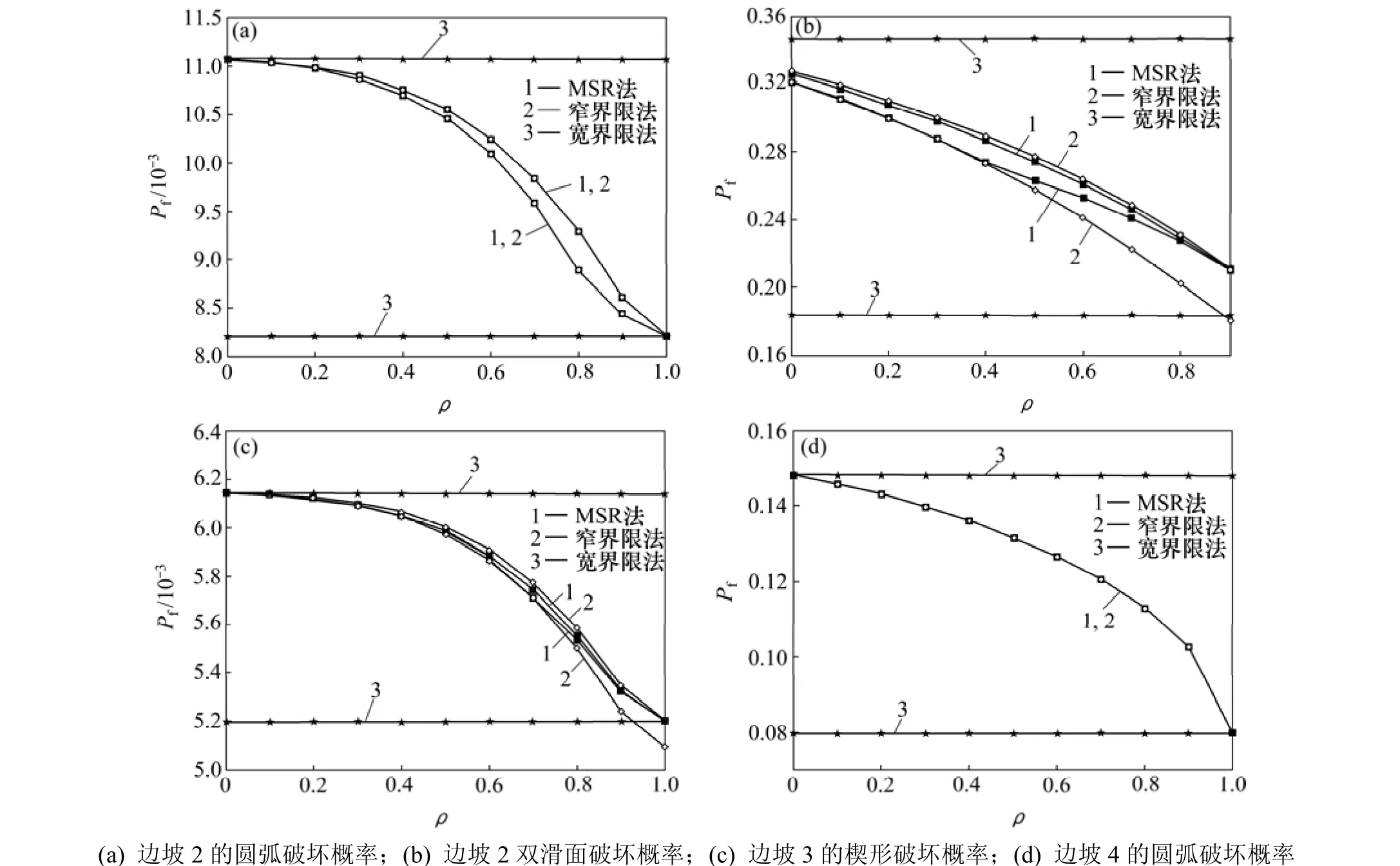
图2 “超构件”的失效概率区间Fig.2 Failure probabilities bounds of super-components

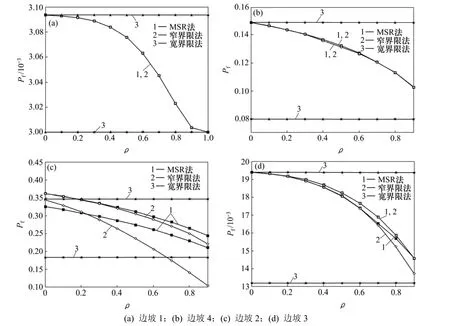
图3 边坡的体系失效概率估计区间Fig.3 System failure probabilities of slopes

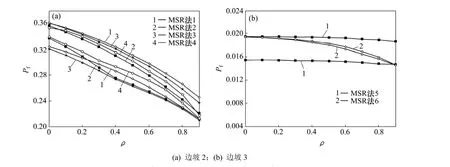
图4 多尺度MSR法的边坡子体系失效概率比较Fig.4 Sub-system failure probability calculated by multi-scale method and MSR method

4 讨论

从表2和图2、图3的失效概率区间对比情况可知：宽界限法的区间比其他2种方法的大，其计算精度难以满足工程实际要求。比较剩余两者方法，当失效模式较少时，MSR法与窄界限法的区间均很窄，可较精确地确定体系的失效概率；当失效模式较多时，窄界限法的区间明显拉大，甚至出现不可能概率(如边坡2在饱水状态下的体系失效概率区间已超越边坡1的失效概率区间)，说明窄界限不适合构件较多或构件失效概率较大的体系可靠性评估；MSR法在上述情况下仍能获得符合工程要求的失效概率区间，表明MSR法在应用上不受概率和构件数量的限制。

比较图4中(a)和(b)可以发现：多尺度法导致了概率区间有所增大，即结果精度稍降低。原因是：采用多尺度法过程中，丢失了部分构件的概率信息，即优化求解中的约束条件减少，使求解范围变大，故所得结果的区间可能会增大，这也正是图 3(c)中在相关性较小时采用本文方法比窄界限法的区间稍大的原因。然而，通过引入“超构件”，将边坡 2的体系构件由28个降低到23个，边坡3的体系构件由25个降到23个，大大降低了优化过程中的计算量，提高了计算效率。若不采用多尺度法时，整个工程体系的优化变量数为218个，远远超越了MATLAB中LP工具所能处理的范围，故多尺度法成为了采用 MSR法计算该边坡失效概率的必然选择。

5 结论

(1) MSR法可以考虑2个或多个失效模式之间的相关性，且采用优化方法计算失效概率的边界，所得界限是在给定信息下能确定的最窄边界，故其结果比常规体系可靠度计算方法的结果更精确。

(2) 采用MSR法计算具有相关性的体系失效概率时，计算结果的精度会受到失效模式的影响。在构件概率信息一致时，随着失效模式增多，体系的失效概率估计区间将逐渐增大。

(3) 将多尺度方法与MSR法相结合可能会使体系概率区间稍有增大，但大大降低了 MSR法在优化计算中的工作量，扩大了 MSR法的应用范围，为解决复杂边坡体系可靠度计算的难题提供了新的途径。

[1]Einstein H H. Risk and risk analysis in rock engineering[J].Tunneling and Underground Space Technology, 1996, 11(2):141−155.

[2]Pind R J, Roberds W J. A risk-based approach for the design of rock slopes subject to multiple failure modes-illustrated by a case study in Hong Kong[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2): 261−275.

[3]Duzgun H S B, Yucemen M S, Karpuz C. A methodology for reliability-based design of rock slopes[J]. Rock Mechanics and Rock Engineering, 2003, 36(2): 95−120.

[4]Mukshed A, Robert E M. Gradient and parameter sensitivity estimation for systems evaluated using Monte Carlo analysis[J].Reliability Engineering and System Safety, 2006, 91(5):594−601.

[5]Sung E C. Effect of spatial variability of soil properties on slope stability[J]. Engineering Geology, 2007, 92(3/4): 97−109.

[6]Bhattacharya G, Jana D, Ojha S, et al. Direct search for minimum reliability index of earth slopes[J]. Computers and Geotechnics, 2003, 30(6): 455−462.

[7]Oka Y, Wu T H. System reliability of slope stability[J].Geotechnical Engineering, ASCE, 1990, 116(8): 1185−1189.

[8]Chowdhury R N, Xu D W. Geotechnical system reliability of slopes[J]. Reliability Engineering and System Safety, 1995,47(3): 141−151.

[9]Jimenez R R, Sitar N, Chacón J. System reliability approach to rock slope stability[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 847−859.

[10]谭晓慧. 多滑面边坡的可靠性分析[J]. 岩石力学与工程学报,2001, 20(6): 822−825.

TAN Xiao-hui. Reliability analysis on a slope with several slips surfaces[J]. Chinese Journal of Rock Mechanics and Engineering,2001, 20(6): 822−825.

[11]吴震宇, 陈建康, 许唯临, 等. 岩质边坡稳定的体系可靠度分析及工程应用[J]. 四川大学学报, 2008, 40(2): 32−37.

WU Zhen-yu, CHEN Jian-kang, XU Wei-lin, et al. System atic reliability analysis of rock slope stability and its engineering application[J]. Journal of Sichuan University: Engineering Science Edition, 2008, 40(2): 32−37.

[12]Kang W H, Song J, Paolo G.. Matrix-based system reliability method and applications to bridge networks[J]. Reliability Engineering and System Safety, 2008, 93(11): 1584−1593.

[13]Song J, Kang W H. System reliability and sensitivity under statistical dependence by matrix-based system reliability method[J]. Structure Safety, 2008, 31(2): 148−156.

[14]Song J, Der A K. Bounds on system reliability by linear programming[J]. Journal of Engineering Mechanics, 2003,129(6): 627−636.

[15]Bertsimas D, Tsitsiklis J N. Introduction to linear optimization[M]. Nashua: Athena Scientific, 1997: 18−87.

[16]Armen D K, Song J. Multi-scale reliability and updating of complex systems by use of linear programming[J]. Reliability Engineering and System Safety, 2008, 93(2): 288−297.

(编辑 赵俊)

System reliability analysis of slopes based on multi-scale MSR method

XIE Gui-hua1,2, ZHANG Jia-sheng2, LIU Rong-gui1, LI Ji-xiang3

(1. Faculty of Science, Jiangsu University, Zhenjiang 212013, China;2. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;3. Department of Civil Engineering, Wuhan Polytechnic University, Wuhan 430023, China)

In order to solve the problem that general system reliability methods can hardly be applied to calculate the stable reliability of complex slopes with multiple failure modes, the matrix-based system reliability method (MSR method) was studied. With multi-scale method, the slope system was decomposed into many parallel sub-systems which were regarded as “super-components” so as to decrease optimal variables and reduce the scale of matrixes. A project case of a mine slope system was analyzed. The results show that the results by the MSR method are more accurate than that by general system reliability methods; that combining with the multi-scale method, reliability analysis of complex slopes with multi-failure mode can be well carried out and the scope of systems analyzed by MSR method is expanded; and that the system probabilistic intervals are enlarged slightly by the proposed method while the calculation load is alleviated exponentially. Furthermore, such tasks as matrix operation and optimization calculation can be performed by means of existing calculation software, making the slope reliability assessment more convenient.

complex slope; system reliability; MSR method; multi-scale

TU457

A

1672−7207(2010)06−2400−07

2009−09−13；

2009−12−03

湖北省教育厅重大项目(Z200618001)；江苏大学校级基金资助项目(10JDG097)

谢桂华(1976−)，女，湖南双峰人，博士后，讲师，从事岩土工程可靠性研究；电话：13862441310；E-mail: jg97xieguihua@163.com