浅谈曲线桥梁设计

赵国强

(天津晟兴交通勘察设计有限公司,天津 300251)

随着我国现代化建设及交通事业的蓬勃发展,高速公路、城际立交等的兴建,曲线桥梁得到了广泛的应用。其结构线条平顺、流畅、明快,给人以美的享受。在公路建设中,除特大桥梁外,一般要求桥梁的平面布置服从公路线形,在进行平、纵、横三方面综合设计时,应做到平面流畅、纵坡均衡、横断面合理,并避免长直线设计,此时,曲线梁桥往往成为最优方案。另外在山区公路展线,城市桥梁避开管线、文物,节省拆迁费用,减小建筑用地等方面有直接可观的经济效益。因而曲线梁桥有着广阔的应用前景。

1 曲线梁的基本尺寸拟定

曲线连续梁桥,截面形式一般都采用箱形截面,因为箱形截面具有较大的抗弯刚度和良好的抗扭性能,对用于扭矩较大的曲线梁桥具有突出的优点。跨径一般在20～60m,高跨比一般可取 1/15～1/30,曲率半径在满足路线要求的前提下,越大越好,并与周围环境相协调。曲梁箱形截面多采用单箱单室、单箱双室、双箱单室、双箱双室等截面形式。宽度10 m以内的匝道桥及单向双车道桥梁建议采用单箱单室。

(1)顶板的厚度一般取 18～30 c m,跨中底板厚度取 16～25 c m,桥墩处顶、底板厚度应比跨中厚度大 10 c m以上,以满足钢束布置需要。

(2)腹板的厚度与钢束(或骨架钢筋)数量有关,通常由每排布置的钢束(或钢筋)数量而定,跨中腹板厚度常取 45 c m左右,支点部位应根据具体情况加厚,适应钢束锚固及平弯需求。

(3)腹板和顶底板之间设梗腋,它可以显著提高截面的抗扭刚度和抗弯刚度、增加角隅的联结刚度、减小截面的畸变应力,对顶板而言,增大了板的支点刚度,减小了顶板跨中弯矩,使剪力流的过渡平顺,顶底板钢束布置构造需求,减小板厚。顶板处的梗腋一般采用 3∶1左右,底板处一般采用1∶1。

(4)翼缘板宽度的设计也很重要,过宽的翼缘板会出现“剪力滞后”现象[1],增大结构的分析难度,较窄的翼缘板会导致截面设计不合理。设计时宜合理地加大板宽,使翼板承担较多的板内横向负弯矩。翼板宽度宜取梁宽的 1/3～1/4,端部厚度一般取 10c m,需张拉横向预应力筋时应适当加厚,根部可取 30c m以上。

2 实例内力计算分析

弯曲箱梁一般采用有限元软件进行计算,常用的建模方法有:梁单元法、板壳单元、实体单元法以及梁格法。细分的板壳元和实体单元法计算极为准确,但建模麻烦,计算时间长,结果处理繁琐,且计算结果无法直接与现行规范配套使用。梁单元法计算曲梁非常简单,计算结果也容易与现行规范配套使用;但是对于桥宽/曲率半径 R较大,支点间的曲率角较大的情况,计算结果不能反映弯扭耦合作用及内外腹板的受力不均,更无法反映箱梁的畸变和翘曲,计算精度无法满足工程需要。等效梁格法虽然也不能反映箱梁的畸变和翘曲,但是能反映箱梁的弯扭作用及内外等效梁格的受弯程度的差异。且对于一般的设计,其计算精度是足够的。

2.1 实例桥梁概况

3×20钢筋混凝土箱梁,曲线半径 R=60 m,桥梁宽度 8 m,C 50混凝土,HR B335钢筋,截面尺寸见图 1。

图 1 梁截面尺寸(对称截面,给出一半)

2.2 单梁模型

首先采用单梁法建立模型,1 m一个单元,共划分为 60个单元。端支点采用抗扭支承(对称布置,内侧采用单向支座,外侧采用双向支座,支座中心到截面中心距离 1.5 m),中墩支点采用点铰支承,中支点向外横向偏移一定距离 b(一般取 e的 2倍左右),可以有效降低边跨箱梁的扭矩绝对值,中跨箱梁扭矩相对较小。

使用单梁建立曲线模型时,是以直代曲,不能反映曲梁重心向外偏移对主梁产生扭矩作用。找到曲梁重心偏移截面形心(剪力中心)的距离e,然后在重心位置施加竖直向下偏心均布荷载 q,并在剪力中心位置施加竖直向上的均布荷载 q,重力集度 q=112.2k N(图 2)。

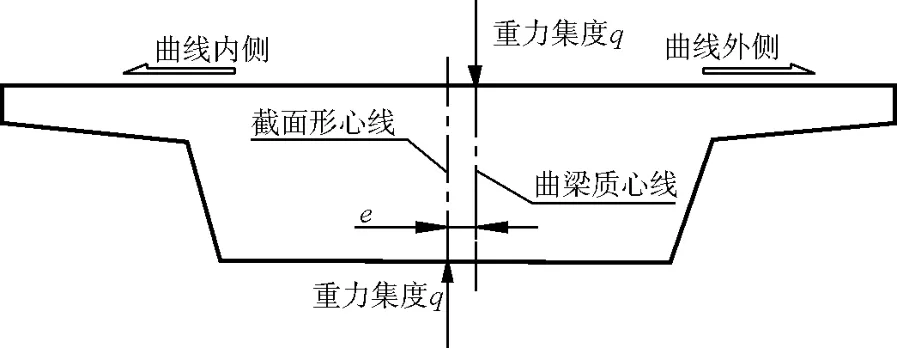
图 2 曲梁扭矩加载示意

简化箱梁截面,按照矩形板考虑,进行质心到形心的偏移距离 e的推导。

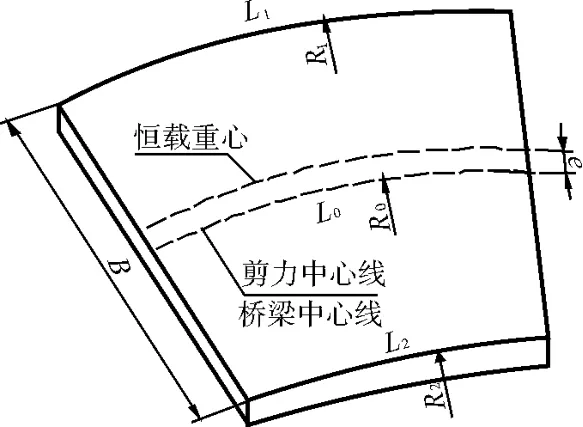
图 3 矩形板截取微元示意

径向截取微元 L0,其平面形状可以视作等腰梯形,如图3所示,则重心到下底距离 c

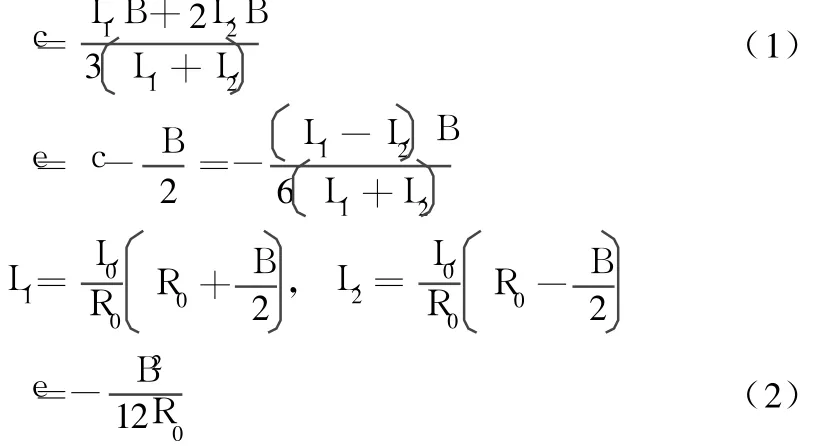
本例 e=0.09 m,支座外偏距离 b=0.18 m

2.3 梁格模型

按照等效梁格建立曲梁模型,如图 4所示。

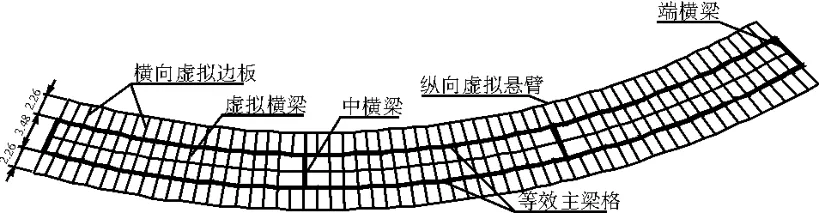
图 4 梁格划分

箱梁中心对称分割为主梁格,每隔 1 m划分一个单元;虚拟横梁采用二字形矩形板截面,每米布置一道,虚拟横梁重量为 0;为了计算中横梁及端横梁内力包络图,稍微细分中横梁和端横梁,横向悬臂板采用变截面矩形板模拟,每米布置一道;并建立虚拟悬臂纵梁把横向悬臂板纵向联系起来。

2.4 作用荷载

考虑自重,二期恒载 56 k N/m(梁格模型主梁格加载铺装荷载集度 20k N/m,纵向虚拟悬臂梁加载护栏荷载集度 8 k N/m;系统升温 20°,系统降温 20°;升温梯度5.5,降温梯度;单车道公路Ⅰ级荷载,其中车道荷载分别定义中心布载、曲线外侧布载,曲线内侧布载三种子荷载工况,由程序自动组合最不利情况;支座不均匀沉降 ±6 m m。

2.5 内力提取及后处理

按照《公路桥涵设计通用规范》进行荷载组合,分别提取两个模型中承载能力极限状态最大正负弯矩、支点边缘剪力、1/4跨中剪力、跨中剪力、扭矩、支反力;提取长期荷载及短期荷载组合下最大正负弯矩。然后按照钢筋混凝土设计理论,进行配筋计算,并进行裂缝验算。计算结果需满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》。具体计算限于篇幅限制,这里不再赘述。

2.6 横梁及桥面板计算

梁格模型中可以直接提取中横梁、边横梁内力包络图,进行配筋计算。单梁模型无法直接提取横梁内力,通常可使用腹板剪力法或等效剪力法等简便方法计算横梁内力。通过建立实体空间有限元模型,计算对比发现:腹板剪力法计算结果较为符合实际,满足工程精度需求。

腹板剪力法就是把支点反力看做是腹板剪力作用给横梁造成的,这样可以按照结构力学计算横梁内力。

如果桥面宽度较大时,尚需验算桥面板。一般方法:(1)按《公路钢筋混凝土及预应力混凝土设计规范》4.1.2～4.1.6计算;(2)截取梁截面单位长度,采取带支承框架分析方法[1]。

2.7 支座选取、布置

依据竖向支反力大小选用支座型号,通常 3跨连续梁,中墩支点采用点铰支承(固定支座,或一个采用固定支座,一个采用单向支座)。端支座采用抗扭支承(双支座,桥面较宽时可采用三或三个以上支座),端支座一般中间支座或内侧支座采用单向支座,其余采用双向支座,这样可以减小温度应力的影响。如果联长较长时,可以增设中墩抗扭支座,增强结构的抗扭能力。

2.8 桥墩验算

一般需要考虑上部结构作用在桥墩上的径向及切向反力,按压弯构件验算。

2.9 对比,总结

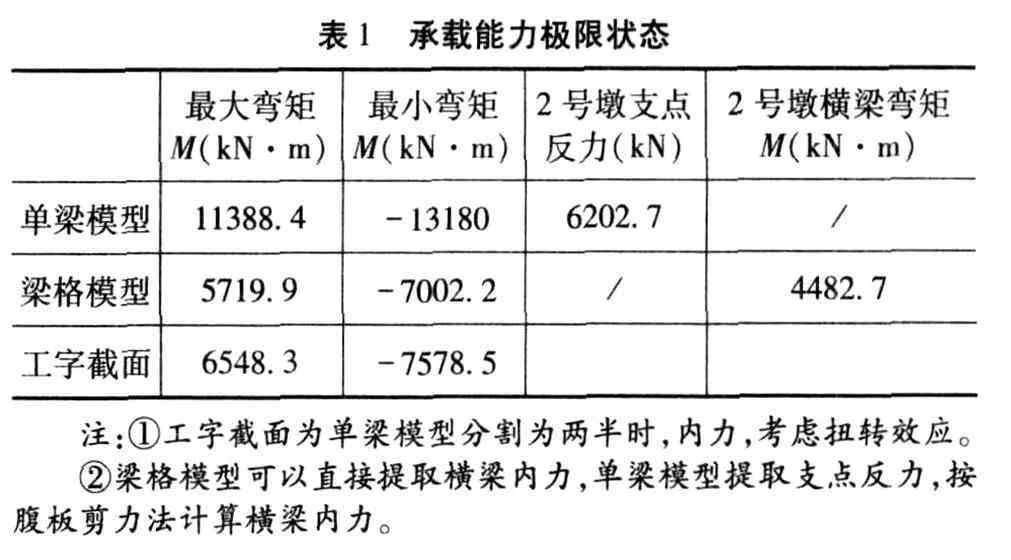
提取以下计算数据,见表 1、表 2,进行数据对比分析。

?

?

参照国外规范,使用单梁模型计算弯梁竖向弯矩时,我们乘以弯矩的不均匀分布系数 1.15,然后除以 2,得单个工字型截面梁的内力,然后按工字型截面计算配筋,需考虑翼缘板的有效宽度[3]。

由单梁模型支反力计算横梁弯矩

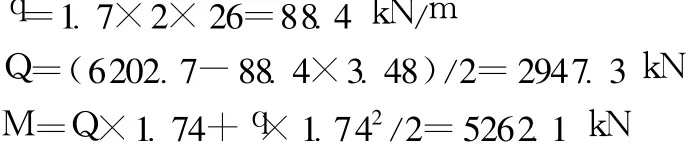
q为中横梁横向均布荷载集度;Q为单个腹板剪力;M为横梁弯矩。

支点间的曲率角 <20°,则扭矩对弯矩的影响是微小的[4],接近直线梁桥,此时曲梁弯矩修正系数 1.15较为保守。

本例支点间的曲率角为 19°<20°,可以不考虑弯矩的增大系数,这样两种模型计算结果更加接近,但是出于安全的角度考虑,一般仍然应乘以该系数。

本例按腹板剪力法计算横梁弯矩较梁格法计算结果要大 17%,这样计算偏于安全。对于钢筋混凝土横梁而言,弯矩保守点还可以,对于预应力横梁,这样保守可能造成上缘产生拉应力,此时需要按照梁格法或者实体模型计算。

3 曲梁病害及预防

值得一提的是曲梁的两种重要病害:支座横向爬移,端支座(内侧)局部或全部脱空现象,特别是在支点间曲率角较大且桥面宽度较小的情况更容易出现。

计算研究表明:恒载作用下,箱梁向外翻转;升温时,端支座向外爬,中墩支座向内爬,箱梁向外翻转;降温时,端支座向内爬,中墩支座向外爬,箱梁向内翻转;升温梯度,箱梁向外翻转;降温梯度,箱梁向内翻转;移动荷载布置在曲线外侧,箱梁向外翻转;预应力作用下,箱梁向外翻转,端支座内侧容易出现拉力。

考虑以上各种荷载效应,按规范进行组合,尽量保证端支座(内侧)不出现拉力,且内侧支座的横向反力 Nw(一般内侧支座采用单向支座,外侧采用双向支座)不超过支座横向约束能力。如果采用板式橡胶支座就要满足:

μ为橡胶支座摩擦系数;f为内侧支座与横向反力 Nw相同荷载工况下的竖向反力。

然而端支座(内侧)在发生较大横向约束时,大多数情况下(箱梁向外翻转)竖向反力较小,故板式橡胶支座并不能很好的阻止支座的横向爬移现象。

常用的防止曲梁爬移破坏的方法是通过特殊措施增大梁端双支座之间的距离,最好是箱梁外侧在端部加宽,再将外侧支座向外偏移,同时适当向外偏移中支座位置,以抵消曲梁部分横向扭矩的影响。内侧支座也可向内侧偏移,但效果没有偏移外侧支座明显。这种方法几乎不增加成本,就能很好的避免内侧支座脱空现象,有效增强端部梁体的抗扭性能。

4 结束语

对曲线梁的基本受力特征进行分析总结,有助于结构设计的宏观把握;详细的介绍了两种实用计算方法;并进行了对比分析,总结两种方法的优缺点及适用范围;算例中除了离心力[2]没有考虑以外,荷载考虑比较周全,实用性较高。

[1]郭金琼.箱形梁设计理论[M].北京:人民交通出版社,1991

[2]J T GD 60-2004公路桥涵设计通用规范[S]

[3]J T GD 62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S]

[4]E·C·汉勃利.桥梁梁上部构造性能[M].北京:人民交通出版社,1982