关于双平面镜成像特性的研究*

朱庆华 顾菊观 钱星星 俞 琼 高慧芝

(湖州师范学院理学院 浙江 湖州 313000)

引言

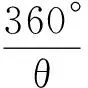
1 双平面镜的成像规律

1.1 成像区域

如图1所示，双平面镜的两平面镜夹角为θ(0°≤θ≤180°)，两平面镜分别记为A、B，以平面镜A所在直线为极轴建立极坐标系，则光源S所在的位置可以表示为S(R,α),R为光源到坐标原点的距离.物体能在平面镜中成像，须满足条件为物体在平面镜前.所以，不可再次成像区域为∠A′OB′所夹区域,其余均为可成像区域.

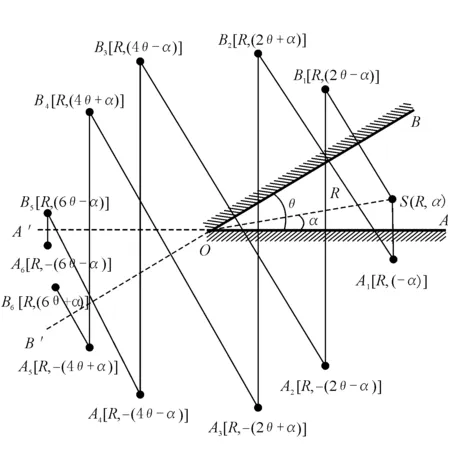
图1 双平面镜成像示意图

1.2 像点的位置

S经双平面镜所成像点的位置可以在极坐标下表示出来[1].设经A平面镜反射所成的像点记为A1，A2，A3，…An，经B平面镜反射所成的像点记为B1，B2，B3，…Bm.如图1，根据平面镜成像的性质，显然可以得到

同理可得

依此类推可得

所以，S，A1，A2，…An；B1，B2，…BM均落在以R为半径、O为圆心的圆上.经双平面镜反射所成像点在极坐标下的极角如表1所示(以逆时针方向为正).

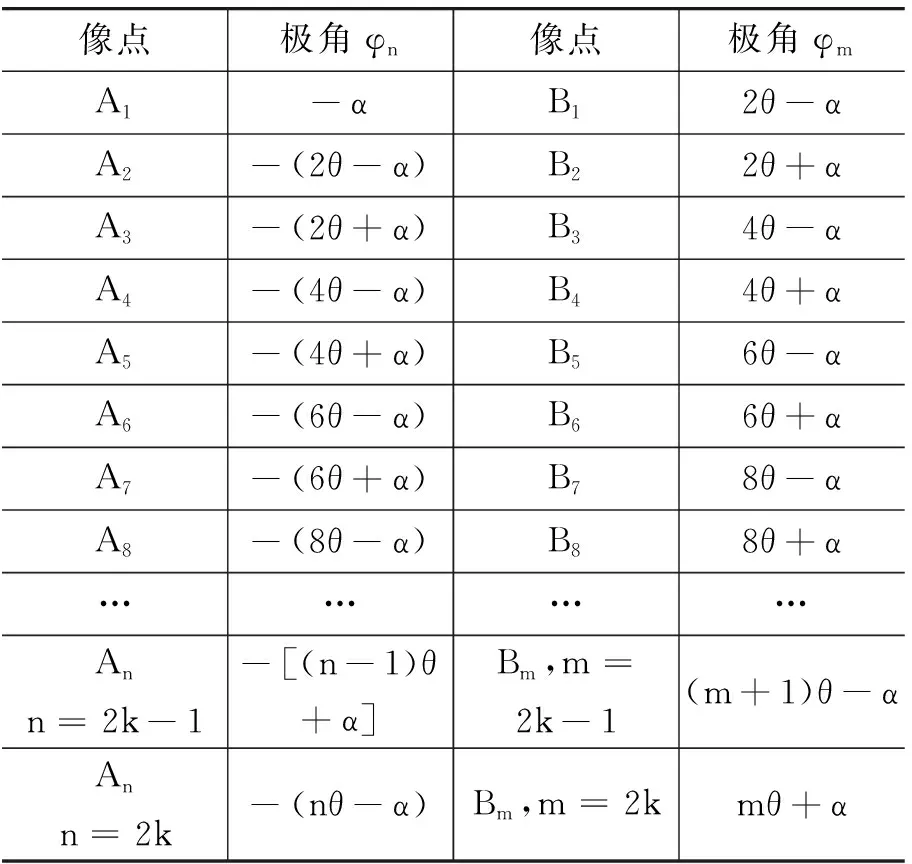
表1 像点的极角

2 成像的个数

2.1 经A平面镜反射形成的像点个数

根据表1，以A平面镜所在直线为极轴，经A反射的像点极角可以表示为

φn=-[(n-1)θ+α]

n=2k-1k=1,2,3,…

(1)

φn=-(nθ-α)

n=2kk=1,2,3,…

(2)

根据图1，有φn≥-180°，依此可分别求得(1)式、(2)式满足该条件的最大整数解，记为n1、n2；取n1、n2中较大的值即为经A反射成像的个数，记为max(n1,n2).

2.2 经B平面镜反射形成的像点个数

同理，经B反射的像点极角可以表示为

φm=(m+1)θ-α

m=2k-1k=1，2，3，…

(3)

φm=mθ+α

m=2kk=1，2，3，…

(4)

此时，需进行坐标极轴的变换，以B平面镜所在直线为极轴，则像点极角为

φm′=mθ-α

m=2k-1k=1，2，3，…

(5)

φm′=(m-1)θ+α

m=2kk=1，2，3，…

(6)

根据图1有，φm′≤180°，依此式可分别求得(5)式、(6)式满足该条件的最大整数解，记为m1、m2，取m1、m2中较大的值即为经B反射成像的个数，记为max(m1，m2).

2.3 像的总数及是否有重合像的判断

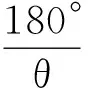
若φn≥-180°和φm′≤180°取到等号，则说明像点落在平面镜所在的直线上，此时经A反射成像个数和经B反射成像个数分别为max(n1,n2)-1和max(m1，m2)-1.

取θ=120°，α=60°和θ=120°，α=75°两种情况为例进行说明.

当θ=120°，α=60°时，不难求得满足条件φn≥-180°的最大n值为2，取到等号，像点落在平面镜A所在直线，故经平面镜A反射成像个数为1个，同理可得经平面镜B反射成像的个数也为1.所以，成像总数为2个.与CAD作图所得结果一致，如图2所示.

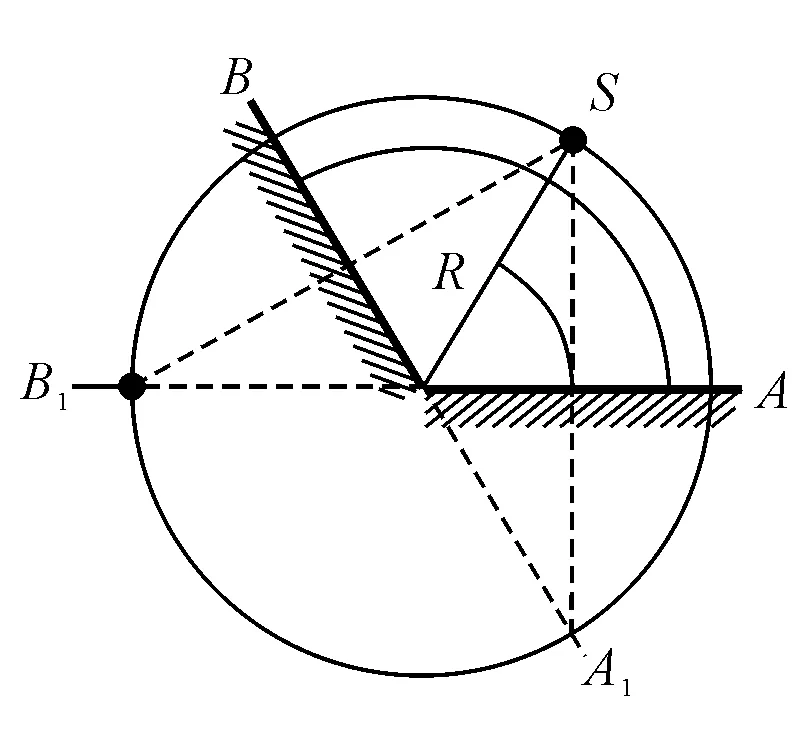
图2 θ=120°，α=60°双平面镜成像

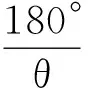
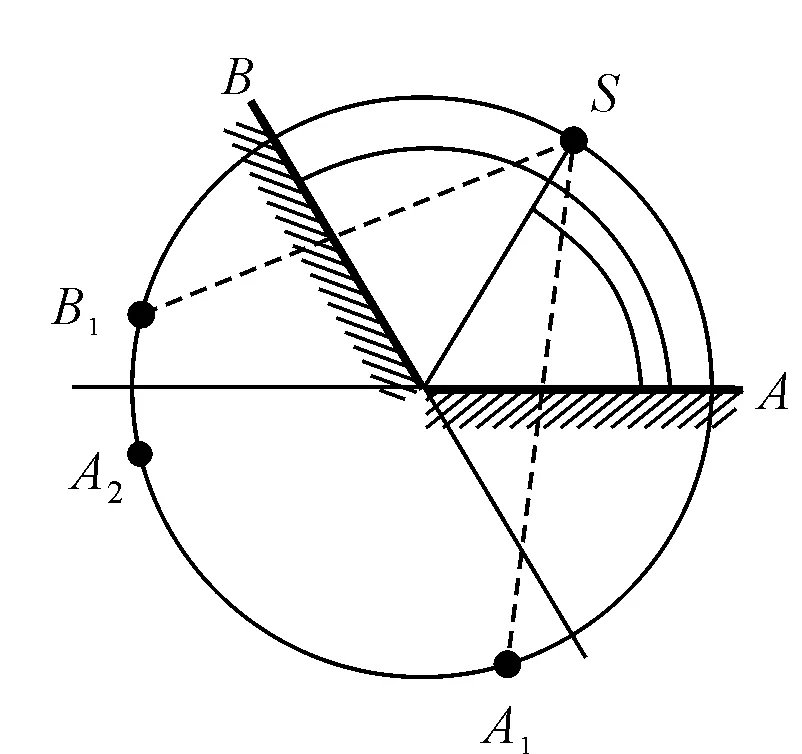
图3 θ=120°，α=75°双平面镜成像

综上，双平面镜成像的个数与两平面镜的夹角θ以及光源在两平面镜间的位置α有关；故只要给定θ(0°≤θ≤180°)和α的值，就可以根据上述给出的理论计算方法求出任意情况下的像点个数，且与实际作图结果一致.

参考文献

1 林遂弟.两个互成角度的平面镜成像规律的研究.物理教师，2001，22(10)：16～17

2 邬剑峰.两个互成角度的平面镜中能形成多少个像.中学物理教学参考，2003，32(7)：20