论高斯的几何学思想及其意义

陈惠勇

(江西师范大学 数学与信息科学学院，江西 南昌 330022)

1827年高斯《关于曲面的一般研究》一书的发表，标志着内蕴微分几何学的创立。高斯在这篇文章中提出了一个全新的观念——一个曲面本身就是一个空间！并从曲面本身的度量出发，展开曲面的内蕴几何研究，得出了决定曲面在空间的形状等一系列的理论与方法。在高斯的几何学思想中有几个核心概念：即直线与测地线；平行公设的否定与弯曲空间概念的产生；第一基本形式与弯曲空间的度量；曲面的度量与曲面在空间的形状。正是由于这些核心概念以及高斯的绝妙定理和高斯-博内定理等的揭示，才真正揭示出非欧几何的本质。高斯的思想后经黎曼等人的发展，推广到高维情形——黎曼几何学。20世纪，黎曼几何学已成为爱因斯坦广义相对论的数学基础。本文考察了高斯几何学思想中几个核心概念的发现及其意义，并由此探究高斯几何学思想的思维轨迹。

一、直线与测地线

几何学研究的基本出发点是点、线、面等基本元素。在《几何原本》中，欧几里得首先给出它们的定义：“点是没有部分的；线只有长度而没有宽度；一线的两端是点；直线是它上面的点一样平放着的线”[1]。欧氏几何所讨论的点、线是数学上抽象的点和线。欧几里得的直线概念是非常朴素而且是直观地描述的，并且定义中的线是指直线段。如何理解“直线是它上面的点一样平放着的线”，“线只有长度而没有宽度”，也就是如何理解直线的概念。从欧几里得在定义19中关于直线、三边形等的定义，以及第一卷命题20“在任何的三角形中，任意两边之和大于第三边”等中可以看出，就是对“长度”的概念必须有一个确切的定义。欧氏几何的直线，其本质是平面上任意两点之间的最短线。

事实上，要给直线下一个精确的定义几乎是不可能的。希尔伯特在他著名的《几何基础》中，建立了历史上第一个完备的公理化体系，第一次明确提出了选择和组织公理系统的三大原则：相容性、独立性和完备性。他真正抓住了几何元素的本质——公理系统的逻辑结构与内在联系。希尔伯特并不给出点、线、面等几何基本概念的定义，而是将它们叫做空间几何的元素或空间的元素，并设想点、线、面之间有一定的相互关系，用“关联”(“在……之上”、“属于”)、“介于”(“在……之间”)、“全同于”(“全合于”、“相等于”)等词来表示，并用几何公理——关联公理(结合公理、从属公理)；顺序公理(次序公理)；合同公理(全合公理、全等公理)；平行公理和连续公理——将这些关系予以精确而又完备的描述。这样，在希尔伯特的几何体系中，所有的问题就有了一个严格的逻辑基础和起点。在《几何基础》的附录1“直线作为两点间的最小距离”一文中，希尔伯特提到“无处是凹的体”并给出这一概念的定义：“无处是凹的体系指具有下述性质的一个体：假如在其内部两点用以直线相连，则此直线介于这两点的部分将整个位于这个体的内部”[2]。从这里可以看出，直线的性质是作为两点之间的最短距离，而这一性质只有在“无处是凹的体”的概念下才是成立的，也就是说只有在欧氏空间(平直的、刚性的)的意义下这一性质才是成立的。

高斯的内蕴微分几何学思想渊源于几何基础的研究，而其直接的现实渊源则是关于大地测量工作的。“高斯从事的整个大地测量工作和这方面的研究都是和完成汉诺威弧度测量相关联的。虽然这个本身弧长只有2.1°的弧度测量对决定地球形状和大小不能起很大作用，然而，在19世纪，对科学地设计和实施高精度的大地测量工作却起着巨大的指导作用”[3]。

从现代微分几何学的观点来看，高斯的大地测量本质上是度量曲面上(地球表面)与外在空间无关的两点之间的最短距离(弧度)的问题，这就很自然地得出测地线的概念，即“在一个给定的曲面上的关于最短路径的理论”[4]。测地线就是曲面上具有零测地曲率的曲线，因而，测地线的切线向量沿测地线本身是平行地移动着的，当一条测地线的包络可展曲面展开到平面时，测地线就成了直线。高斯的测地线概念就是欧氏几何中的直线概念在弯曲曲面上的自然推广。

二、平行公设的否定与弯曲空间概念的产生

M.克莱因指出：“有关非欧几里得几何的最大事实是它可以描述物质空间，像欧几里得几何一样地正确。后者不是物质空间所必然有的几何；它的物质真理不能以先验理由来保证。这种认识，不需要任何技术性的数学推导，首先是由高斯获得的”[5]。高斯正是由于早年对几何基础问题的深入研究，才导致了弯曲空间概念的产生，进而揭示了空间的非欧本质。

我们知道，对平行公设的否定是这一理论的突破口。勒让德(A.M.Legendre)于1794年首先指出三角形的内角和等于180°的定理等价于欧氏几何的第五公设。就在这一年，高斯已经有了关于这些问题的第一个深刻思想。高斯于1846年10月给Gerling的信中写道：“在任何的几何中，一个多边形之外角和在数量上不等于360°，……而是成比例于曲面的面积，这几乎是这一理论之开端的第一个重要定理，这个定理的必要性我已于1794年认识到了”[6]。高斯的这一深刻思想，至少包含三层意思。

第一，平行公设的否定。在欧氏几何中，三角形内角和等于180°与其外角和等于360°是等价的，一般地有任意一个多边形之外角和在数量上也等于360°。高斯所讨论的是双曲几何学情形，这里所说的“在任何的几何中，一个多边形之外角和在数量上不等于360°……”实际上就是对平行公设的否定。

第二，弯曲空间概念的产生。三角形内角和等于180°的定理，本质上是说平面是平坦的而不具有曲率。高斯在此所得到的认识：“一个多边形之外角和在数量上不等于360°，而是成比例于曲面的面积”，这一比例就是高斯曲率。用现代的语言表达就是，在球面几何学情形，三角形的三内角之和必然大于180°，并且有一个非常重要的公式A+B+C-π=S/R2，这里S为面积，R是球面的半径，而1/R2则是度量球面的高斯曲率；在双曲几何学情形，三角形的三内角之和必然小于180°，并且有如下的重要公式A+B+C-π=-S/R2，S为面积，此时R2代表非欧几何的一个绝对的度量，换句话说，在非欧几何的平面上，它的高斯曲率是负的且等于-1/R2；很显然，如果上述的比例为零(也就是高斯曲率为零)，那么自然地得出“多边形之外角和在数量上就等于360°”，也就是三角形内角和等于180°的定理，这就是欧几里得几何情形。

由此可知，是否满足欧几里得的平行公设所体现出的本质乃是所论几何空间是否为弯曲的性质。因而，高斯于1794年所得到的关于这些问题的深刻认识，表明在高斯的头脑中已经有了“弯曲空间”的概念。

第三，“这几乎是这一理论之开端的第一个重要定理”。高斯在这里所说的“这一理论”指的是他所发现的“双曲几何学”，而这个重要定理就是高斯-博内定理，它是非欧几何学的重要定理，也是内蕴微分几何学的一个极端重要的定理。这一定理被高斯誉为“整个曲面理论中最优美的定理”，它对微分几何学的发展和影响是非常深远的[注]陈省身于1944年给出了高维高斯-博内公式的内蕴证明，成为现代微分几何学的出发点，其思想与方法对整体微分几何的发展有着深刻的影响。。

如果联系高斯《关于曲面的一般研究》对高斯-博内定理的高度重视，特别是高斯运用这一定理于测地三角形的角度比较定理与面积比较定理的研究以及实际测量测地三角形等等，我们可以看出高斯的真正用意是验证他所发现的非欧几何[注]高斯用了其《关于曲面的一般研究》中的最后九节(第21-29节，大约占了整篇文章的三分之一)的篇幅几乎全部用于比较定理的证明。这些比较定理一方面把单个的角(不仅仅是角度之和)与欧几里得平面上具有同样长度的直边形三角形的角进行比较；另一方面，还把曲面上测地三角形的面积与欧几里得平面上具有同样长度的直边形三角形的面积进行比较。。

三、第一基本形式与弯曲空间的度量

几何学研究的一个基本问题或出发点是度量问题。高斯关于几何基础问题的研究所发现的弯曲空间概念在数学上是如何刻画？特别是高斯后来的大地测量工作必须解决的测地线的度量问题等，都涉及到几何学的一个基本问题——弯曲空间的度量。

欧氏几何中最重要的定理之一的毕达哥拉斯定理之本质乃是几何空间的度量性质，而度量性质可以说是展开所有可能的几何学的基本假设前提。迄今为止，在大部分有意义的几何空间中，都要求这条定理在无穷小的情形下成立。由毕达哥拉斯定理所确定的空间度量是平直(或刚性)空间的度量。因此，如何把度量性质推广到弯曲的空间就成为问题的关键。在高斯以前，曲面或空间曲线的方程式被看作是三个坐标的隐函数，或者是一个坐标表示为其他两个坐标的函数。这种做法实际上仍然是把所研究的曲面或空间曲线嵌入于高一维的空间(即外围空间)之中加以研究的，因而其方法是外蕴的。

高斯几何学思想及其研究的出发点是“从曲面本身的度量出发决定曲面在空间的形状”，因而与外在空间无关，即是“内蕴”的几何学。高斯首先着手把三个坐标看成是另外两个独立参数的函数，这两个参数可以在已知曲面上适当地选择，高斯的这一思想在微分几何学的发展中获得了普遍的公认。早在1822年，高斯解决哥本哈根科学院提出的征奖问题中，就已经系统地运用了这种参数表示的思想[7]。

曲面上任意一点的坐标(x,y,z)可以用两个参数u、ν表示，从而曲面的方程可表示为：r=r(x(u,ν),y(u,ν),z(u,ν))，高斯的出发点是运用这个参数表示来对曲面做系统研究，并首先引进曲面的弧长元素ds，建立了曲面的第一基本形式dr2=ds2=Edu2+2Fdudν+Gdν2(其中E=ru·ru,F=ru·rν,G=rν·rν，称为曲面的第一类基本量)其意义就是，在正确到高阶无穷小范围内，曲面是等长地对应于切平面上的无穷小区域，并且曲面的第一基本形式在切平面上是以ru和rν为基本向量，以du为dν坐标的长度表达式。若曲面上参数曲线网取正交曲线网时，即向量ru和rν垂直时，有F=0，于是曲面的第一基本形式化为：dr2=Edu2+Gdν2。这就是勾股定理。所以说曲面的第一基本形式本质上是勾股定理的推广，或者说勾股定理是第一基本形式在无穷小范围内的近似。

专门研究曲面上由第一基本形式决定的几何学称为内蕴几何学，它在高维的推广就是黎曼几何学。因此，我们说高斯通过推广度量概念引进了第一基本形式，从而解决了展开其内蕴微分几何学的基础——弯曲空间的度量，这是几何学历史上的一次重大的突破。

四、曲面的度量与曲面在空间的形状

1822年，高斯在解决哥本哈根征奖问题时，就已经意识到曲面研究的中心问题是曲率问题。这是高斯内蕴微分几何学理论的突破口，他在寻求曲率的过程中，有两个关键的概念：一是高斯映射的概念；另一个就是角度概念的推广。

在《关于曲面的一般研究》中，高斯首先引进了一个辅助球面，并假定用球面上不同的点表示不同的直线的方向，该方向与以球面上的点为端点的半径平行，这就为后面定义高斯映射奠定了基础。接着高斯给出了一些重要的命题，包括两条相交直线的夹角、两个平面的夹角、一条直线与一个平面的倾斜角、平面的定向以及球面上的点之间的坐标表示的三角公式、球面上的三点以及坐标系的原点组成的锥体的体积公式等等。

关于角度的定义，高斯是将它转化到相应的辅助球面上、相应于直线的方向的球面上两点的弧长来度量的，也就是说，高斯将角度看成是单位圆周的子集而不是一个数。高斯这一观点是符合于几何学的本源的，希腊人最初的想法与此是一致的(而把角度看成数不过是近代的观点[8])，它有利于推广到高维的情形，这种推广就是高斯曲率和总曲率的概念。这里值得指出的是，高斯的这一想法在一些文献中没有得到应有的重视。如Michael Spivak对此就完全忽视了，他说：“This section may be skipped entirely”[9]。

设S1是以O为圆心的单位圆，所谓相交于O点的两条直线的夹角α是指S1上由这两条直线截出的弧长，如图1所示。

图1 相交于O点的两条直线的夹角

而曲线在一点处的曲率就是指角度的增量相对于弧长的变化率，即曲线上无穷小弧段长度与其切映射下像的长度的反比的极限，如图2所示。

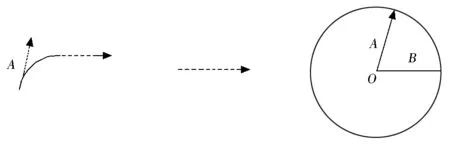
图2 曲线在一点处的曲率

从几何学的观点看，正如我们可以把角度看成二维空间里单位圆周上曲线段的长(弧长)或者一维体积一样，我们也可以将三维空间中单位球面S2上区域的面积或者二维体积看作三维空间角度的表示。一般地，n维空间中的角度被看成单位球面Sn-1上区域的(n-1)维体积。这种想法在高斯的总曲率和曲率测度(即高斯曲率)的定义中起着关键的作用。高斯在他的论文摘要中指出：“如果我们用上述方法来表示球面上各点的法方向，……曲面的一部分对应附属球面上一部分，并且曲面这一部分和平面差别越小时，附属球面上相应的面积就越小。由此，一个十分自然的想法是以附属球面上相应部分的面积作为曲面给定部分的全曲率的度量。因此作者称它为曲面在该部分的总曲率”。接着，高斯定义“曲面在某一点处的曲率测度为一比值，分母为该点处无穷小邻域的面积，分子为附属球面上相应与曲面上的那一部分的面积，即相应的总曲率。”

关于曲率测度的正负号与曲面在该点邻近的形状的关系，高斯指出：“曲率测度对于凹-凹或者凸-凸曲面(这个区别是非本质的)为正，但对于凹-凸曲面为负。如果曲面由每一种的部分所组成，那么在分隔这两种曲面的曲线上，其曲率测度应该为零”[4]。

高斯并得出了曲面在各种表示形式下的高斯曲率的计算公式，特别地，得出了曲面的参数表示形式下的高斯曲率公式，并得出了著名的公式：即高斯曲率仅与第一类基本量及其一阶或二阶偏微分有关，这就是说高斯曲率是由“曲面本身的度量”所确定的。而曲面本身的度量在保长变换下是不变的，因而就有“曲面的高斯曲率是曲面在保长变换下的不变量”，这表明曲面的度量性质本身蕴含着一定的弯曲性质。

这就是说，高斯在他的一般研究中解决了内蕴微分几何学的中心问题——从曲面本身的度量出发决定曲面在空间的形状，这个定理被高斯称为“绝妙的定理”，它是微分几何学发展的里程碑。

五、结语

综上分析，我们可以历史地勾勒出高斯创立内蕴微分几何学的思想轨迹：高斯的大地测量工作，本质是度量地球表面(弯曲的曲面)上任意两点之间的最短距离，这种度量只与曲面本身相关而与其外在的空间无关，这就促使高斯思考这样的问题——“我们是否可以从曲面本身的度量出发决定曲面在空间的形状”？这种思考具有本质的意义，这是高斯内蕴微分几何思想的出发点。高斯正是从这个想法出发，引出曲面的参数表示、曲面上的弧长元素(即第一基本形式)，以及由第一基本形式出发，研究弯曲的曲面上的内蕴几何问题，得到了高斯曲率的计算公式，并进而证明高斯曲率是在等距变换下的不变性质(即高斯的绝妙定理)以及总曲率与测地三角形内角和的关系公式(即高斯-博内定理)等等内蕴微分几何的重要定理。他创立了内蕴微分几何学，开拓出“一块极为多产的土地”。沿着高斯的思路，必然得到这样一个全新的观念——一个曲面本身就是一个空间！在这样的空间(弯曲的)上展开的几何学必定是非欧的，这是高斯最伟大的创造。

在高斯发表《关于曲面的一般研究》一文之后大约100年，爱因斯坦对高斯的这项工作做出了如下的评价：“高斯对于近代物理理论的发展，尤其是对于相对论理论的数学基础所做的贡献，其重要性是超越一切，无与伦比的，……假使他没有创造曲面几何，那么黎曼的研究就失去了基础，我实在很难想像其他任何人会发现这一理论”[10]。我们将高斯于1817年写给奥尔伯斯(Heinrich Olbers)的信中的一段话与爱因斯坦的评价做一对比，其意寓是深长的。高斯说道：“我愈来愈深信我们不能证明我们的几何(欧氏几何)具有(物理的)必然性，至少对于人类理智来说，是人类理智所不能证明的。或许在另一个世界中，我们能洞察空间的性质，而现在这是不能达到的。同时我们不能把几何与算术相提并论，因为算术是纯粹先验的，而几何却可以和力学相提并论”[6]。高斯心中的几何学是和力学相提并论的，这种认识让我们想到黎曼在他著名的《关于几何基础中的假设》中这样一句意味深长的话：“这条道路将把我们引到另一门科学领域，进入到物理学的王国，进入到现在的科学事实还不允许我们进入的地方”[11]。

由此我们可以看到，高斯的内蕴微分几何学和黎曼关于黎曼几何学的构想都是意在揭示欧氏几何不具有惟一的(物理的)必然性，他们关于几何学的思想是一脉相承的，黎曼的几何学思想深受高斯的影响。20世纪微分几何学与理论物理学的发展，以无可辩驳的事实证实了高斯的伟大思想。

参考文献：

[1] 欧几里得.几何原本[M].兰纪正，朱恩宽，译.西安：陕西科学技术出版社，2003.

[2] D.希尔伯特.几何基础(第二版)[M].江泽涵，朱鼎勋，译.北京：科学出版社，1995.108.

[3] [苏]P.D.巴格拉图尼.卡·弗·高斯——大地测量研究简述[M].许厚泽，王广运，译.北京：测绘出版社，1957.16.

[4] C.F.Gauss.Carl Friedrich Gauss Werke Band (Ⅳ)[M].Gottingen：Gedruckt in der Dieterichschen Universitats druckerei (W.F.Kaestner)，1880.238.

[5] [美]莫里斯·克莱因.古今数学思想(第三册)[M].上海：上海科学技术出版社，2002.285-286.

[6] C.F.Gauss.Carl Friedrich Gauss Werke Band (Ⅷ)[M].Gottingen：Gedruckt in der Dieterichschen Universitats druckerei (W.F.Kaestner)，1990.177，266.

[7] 陈惠勇.高斯哥本哈根获奖论文及其对内蕴微分几何的贡献[J].内蒙古师范大学学报(自然科学版)，2007，36(6)：771-774.

[8] D.H.Gottlieb.All the way with Gauss-Bonnet and the Sociology of Mathematics[J].Amer.Math.Monthly，1996，103(6)：457-469.

[9] M.Spivak.A Comprehensive Introduction to Differential Geometry[M].Berkely，CA：Publish or Perish，INC，1997.71-131.

[10] Tord Hall.Carl Friedrich Gauss：A Biography (1970)(中译本)高斯——伟大数学家的一生[M].田光复，译.台北：台湾凡異出版社，1986.100.

[11] 黎 曼.关于几何基础的假设[A].李文林.数学珍宝——历史文献精选[C].北京：科学出版社，1998.601-613.