平面射影几何中二维射影变换不变元素的分布
周明旺
(连云港师范高等专科学校 数学系,江苏 连云港 222006)
二维射影变换是平面射影几何的核心内容之一,主要研究了其不变元素(不变点、不变直线)的存在性和解法,而其不变元素的结合关系则是二维射影变换的核心内容,它归根结底由射影变换的系数矩阵所决定,也就是取决于特征方程的根的分布情况.本文重点讨论了二维射影变换的不变点与不变直线结合关系的分布特征,并给出不变元素的分布对射影变换的影响.文中总假设射影变换的特征方程的根均为实数,即f(λ)=|A-λE|=0或有三个实数根,或有一个实数根和一对共轭虚根.
1 预备知识
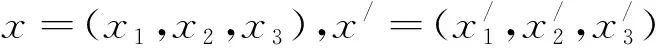
(1)
则称φ是π到π/的二维射影对应;特别地,若π/=π,则称φ是π上的二维射影变换.
利用线性代数知识,(1)不仅给出了两个点场之间的射影对应,而且也同时给定了同底两线场之间的射影对应,共诱导了下列四个式子:

表1 二维射影变换诱导公式表
其中Aij为aij的代数余子式,由(1)的限制条件|A|≠0,ρ≠0,表1中各对应式的系数矩阵均非奇异,且有比例常数λ≠0,σ≠0,μ≠0.
引理1 二维射影变换(1)有不变元素的充要条件是f(λ)=|A-λE|=0有根.

推论1 二维射影变换(1)至少有一个实的不变点和一条实的不变直线.
2 主要结果
2.1 不变点与不变直线的结合关系特征
定理1 属于三个不同特征根的不变点或不变直线线性无关.
证明 设与射影变换(1)的特征根λi(i=1,2,3)相对应的不变点为xi(i=1,2,3),则(A-λiE)xi=0,即Axi=λixi,(i=1,2,3).
由于无以(0,0,0)为射影坐标的点,所以单个的不变点必然线性无关.
下证属于两个不同特征根的不变点线性无关.假设有
ax1+bx2=0,(a,b∈R)
(2)
成立.
(2)式两端乘以λ2,得aλ2x1+bλ2x2=0,
(3)
(2)式两端施行变换A,即有
aλ1x1+bλ2x2=0
(4)
(4)式减去(3)式,得到a(λ1-λ2)x1=0,
由于x1≠0,λ1-λ2≠0,所以a=0这时(2)变成bx2=0,又x2≠0,所以b=0.这就证明了x1,x2线性无关.
同理可证,属于三个不同特征根的不变点线性无关.
利用对偶原则,属于三个不同特征根的不变直线线性无关.
定理2 两不变点的连线是一条不变直线;对偶地,两不变直线的交点是一不变点.
证明 设与射影变换(1)的两不变直线相对应的特征值为λ1,λ2.由定理1知,λ1≠λ2,又两条直线有且只有一个交点,记为x.假设x为非不变点,则(A-λiE)x=0,(i=1,2)均无解(只有零解),从而|A-λiE|≠0,(i=1,2).这与λi(i=1,2)是|A-λE|=0的根矛盾.
因此,两不变直线的交点是一不变点.
利用对偶原则,两不变点的连线是一条不变直线.
推论 2 不变直线上必存在不变点;对偶地,过不变点必存在不变直线.
定理3 若f(λ)=0有三不等根,则(1)有三个不共线的不变点与三条不共点的不变直线,且每个不变点是其中两条不变直线的交点,每条不变直线通过其中两个不变点.
证明 设f(λ)=(λ-λ1)(λ-λ2)(λ-λ3)=0,λi(i=1,2,3)互不相同.由定理1知,(1)有三个不同的不变点与三条不同的不变直线,且三个不变点不共线,三条不变直线不共点,其中Pi,li属于同一特征根且Pi∉li,(i=1,2,3).再由定理2可知,(1)的每个不变点是其中两条不变直线的交点,每条不变直线通过其中两个不变点.
推论3 若f(λ)=0有三个不等实根,则(1)可简记为
其中ρ1ρ2ρ3≠0.
证明 设相应于特征根λ1所决定的不变点取为新的坐标三点形的一个顶点A1(1,0,0),由(A-λE)x=0得ρ1=a11,a21=a31=0.同理,对其余两个不变点取为新的坐标三点形的另两个顶点,则分别得出ρ2=a22,a12=a32=0和ρ3=a33,a13=a23=0.故结论成立.
定理4 若f(λ)=0有一个二重根,则(1)或有两不变点P1,P2与两不变直线l1,l2,且P1,P2处于l1或l2上,其中有一点是l1与l2的交点;或有一不变点列l1与一不变线束P1且P1∉l1,这时不变点与不变直线均有无穷多个.
证明 设f(λ)=(λ-λ1)(λ-λ2)2=0,其中λ1≠λ2.
1°λ=λ1可决定一个不变点P1与一条不变直线l1.
2°若λ=λ2决定的矩阵(A-λE)的秩为2,则λ=λ2也决定一个不变点P2与一条不变直线l2.这时P1,P2应处于l1或l2上,其中一个是l1与l2的交点,因为P1∉l1,从而一定有P1,P2∈l2(否则l1与l2的交点是不同于P1,P2的不变点或P1,P2的连线是不同于l1与l2的不变直线.矛盾).
3°若λ=λ2决定的矩阵(A-λE)的秩为1,此时,λ=λ2决定无穷多个不变点,其轨迹是一条不变直线且就是l1;对偶地,λ=λ2也决定了无穷多条不变直线,其交点是一不变点恰为P1,此时射影变换称为平面的同调,l1为同调的轴,而P1为该同调的中心.
定理5 设f(λ)=0有三重根,若(A-λ1E)的秩为2,则(1)只有一个不变点与一条不变直线,且不变点在不变直线上;若(A-λ1E)的秩为1,则(1)有一不变点列与一不变线束,且线束顶点在不变点列上.
证明 设f(λ)=(λ-λ1)3=0
1°若(A-λ1E)的秩为2,则(1)只有一个不变点P与一条不变直线l(否则(A-λ1E)的秩不等于2),再由推论2知,P∈l.
2°若(A-λ1E)的秩为1,则λ=λ1决定无穷多个不变点,其轨迹是一条不变直线l,同时λ=λ1也决定了无穷多条不变直线,它们相交于l上一点P(否则,l外就存在有不变点.矛盾).此时射影变换称为扩张,此时同调中心落在该同调的轴上.
定理6 设射影变换φ∶ρx/=Ax,且At=A.则
(1)若射影变换φ有不变点(x1,x2,x3),则φ有不变直线[x1,x2,x3];
(2)若射影变换φ有以[x1,x2,x3]为底的不变点列,则φ有以(x1,x2,x3)为顶点的不变线束.
证明 由(A-λE)x=0,(At-λE)u=0,结合At=A易证.
2.2 不变元素的分布对射影变换的影响
定理7 若射影变换(1)保持x3=0不变,则方程为
|A|=|aij|≠0,ρ≠0.
此时射影变换为仿射变换.

|A|=|aij|≠0,ρ≠0.
若转化为非齐次形式为
显然符合形式
此时射影变换是仿射变换.
定理8 若射影变换(1)保持x3=0上任一点均不变,则方程为
|A|=|aij|≠0,ρ≠0.
此时射影变换为位似变换.
证明 取点P(1,0,0),Q(0,1,0),R(1,1,0)代入(1),得
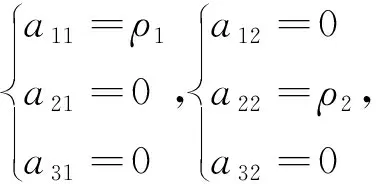
因此,a21=a31=a12=a32=0,a11=a22≠0.此时(1)变为
|A|=|aij|≠0,ρ≠0.
参考文献:
[1]钟集.高等几何[M].北京:高等教育出版社,1983.
[2]方德植,陈奕培.高等几何[M].北京:高等教育出版社,1983.
[3]梅向明,刘增贤,林向岩.高等几何[M].北京:高等教育出版社,1983.
[4]龙泽斌.几何变换[M].长沙:湖南科学技术出版社,1984.
[5]周兴和.高等几何[M].北京:科学出版社,2003.
[6]牛晓奇.二维射影变换二重元素的结构及其特征[J].安阳师范学院学报,2001(5).

