A Generalized Model of Classical Secretary Problem

LIU Xin, JIAN G Peng, L U Ya-nan

(Shenyang University of Chemical Technology,Shenyang110142,China)

In many managerial decision situations such as buying a car,selling a house,or searching for a job,several alternatives are presented sequentially and an accept-or-reject decision is made immediately after evaluating each alternative.The model corresponding to such decision situations under certain assumptions is variously referred to as the secretary problem.The classical secretary problem,which appeared firstin printin Chow et al[1],seems to be the most common name for the sequential evaluation and selection problem,in which one must make an irrevocable choice from a number of applicants whose values are revealed only sequentially.It is also a classic example of a problem amenable to adynamic programming treatment.This article deals with a more generalized version of the classical secretary problem.

1 Notations and Assumptions

Base on the basic assumptions of the model which appear in the references[2]and[3], the structural assumptions made in this generalized model can be summarized as follows:

(1)There are n groups of applicants g1,g2,…,gnapply for one item available,n is known.

(2)Unequal weights qj,j=1,2,…,n may be assigned to each group according to some prior information;the groups are interviewed sequentially in random order,each order being equally likely.

(3)You can rank all the groups from best to worst without ties.The decision to accept or reject a group must be based only on the relative ranks of those groups interviewed so far.

(4)A group once rejected cannot later be recalled.

(5) You are very particular and will be satisfied with nothing but the very best.

Under these assumptions,the question is when to stop the evaluation process and select a candidate.Here the object is to derive the optimal selection strategy,which maximizes the probability of selecting the best group among all choices.

The set Sn={1,2,…,n}represents the order in which n groups or,in more neural terms,choices are interviewed or evaluated. For a given sequence of choices in Sn,we define the jth stage of the evaluation process as the jth choice in the sequence to be evaluated. The best choice in the set Snis called the absolutely best choice,while the best choice in the subset Sj={1,2,…,j}⊂Snis called a relatively best choice at stage j.

Let Q={q1,q2,…,qn},where qj≥0,be the set of weights assigned before evaluations to each choice according to some prior information.The cumulative weight up to and including the jth stage is given by Vj=q1+q2+…+qj,j=1,2,…,n.

2 Main results

At stage n,ps(n)=1,pc(n)=0,p＊(n) =max{ps(n),pc(n)}=1.

Thus,the expected winning probability if we continue at stage j is expressed as a convex combination of p＊(j+1)and pc(j+1)as follows:

j=1,2,…,n-1.

By solving recursively,we have

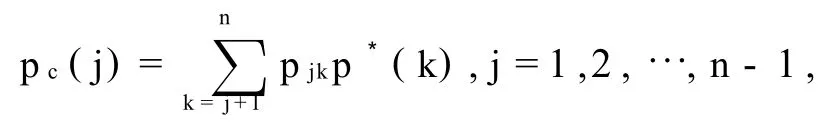
p＊(j)=max{ps(j),pc(j)}=

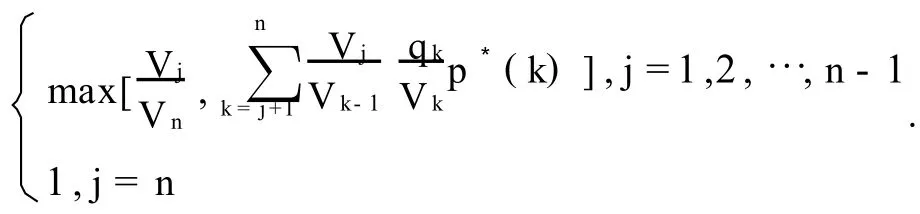
Definition1 The learning set A={k|pc(k)＞ps(k)}and the action set B={k|pc(k)≤ps(k)}.

Lemma1 If j∈A,then,j-1∈A,j=2, 3,…,n.

Proof If j∈A,pc(j)＞ps(j),p＊(j)= pc(j),then pc(j-1)＞ps(j).

Since ps(j)increasing in j,we see that ps(j)＞ps(j-1).

Thus we conclude pc(j-1)＞ps(j-1).

Lemma2 If i∈B,then i+1∈B,i=1, 2,…,n-1.

Proof It is obvious from Lemma1since the subset B is defined as the complement of the subset A.Lemma1and Lemma2together imply that,in this problem,the set Sn={1,2,…,n}can be bisected into two disjoint sets A={1,2,…,j＊-1}and B={j＊,j＊+1,…,n},where j＊is de-fined as the starting stage in the second subset B.

Theorem1 In the optimally divided subsets A={1,2,…,j＊-1}and B={j＊,j＊+1,…,n},the value j＊satisfies the following inequality:

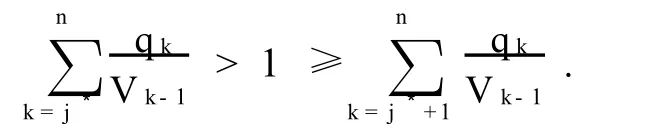
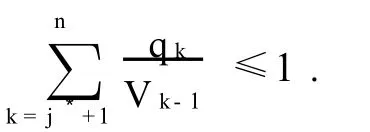
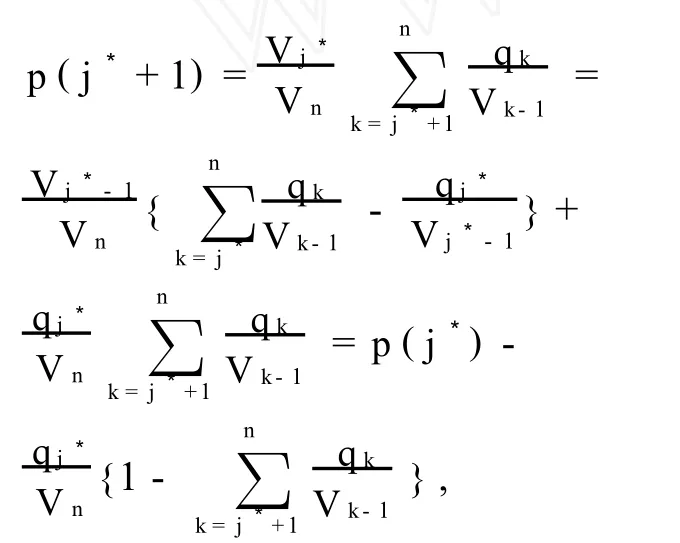
This implies that

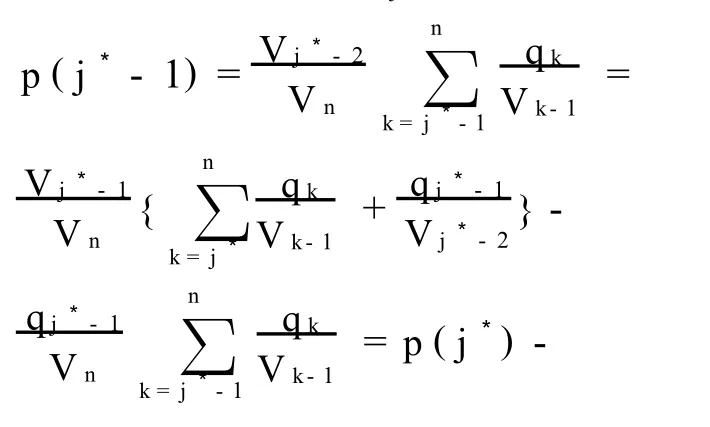
3 Selection Strategy

[1] Lindley D V.Dynamic Programming and Decision Theory[J].Applied Statistics,1961,10:39-51.

[2] Chun Y H.Optimal Partitioning of Groups in Selecting the Best Choice[J].Computer&Operations Research,2001,28(14):1367-1386.

[3] Chun Y H.Selecting the Best Choice in the Weighted Secretary Problem[J].European Journal of Operational Research,1996,92(1):135-147.