对中考中几个亮点试题的赏析
✿浙江省宁波市鄞州区咸祥镇中学 杜开未
对中考中几个亮点试题的赏析
✿浙江省宁波市鄞州区咸祥镇中学 杜开未
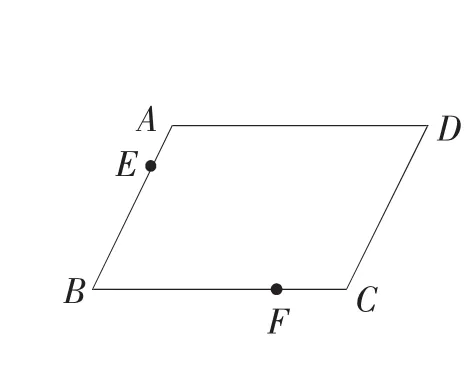
图1-1
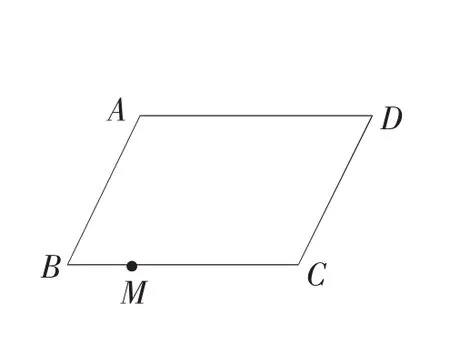
图1-2
在每年中考试题中都能看到很多亮点试题,所谓亮点,应具备:题新不怪、知识常用、视角新颖,方法直观、由易至难、梯度合理,其最大的特色应该是每个学生通过自己的努力都能有不同程度的收获,有助于增强学生答题时的自信心,激发他们的斗志,便于尽情发挥.
一、在熟透知识中考查应变能力——活用等底等高等面积
面积计算中的高、底是学生最熟悉不过的知识,面积的计算又是最简单的公式套用,因此对高、底、积常缺乏深入的拓展研究.活用面积公式中的等底等高等面积,在近几年中考试题中是比较常见的,并且考查范围也越来越广泛.等底等高等面积的作图考查,试题难度不高,却突出了知识的基础、创新、活用等特点.
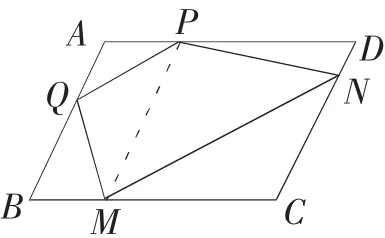
例1:(2008年福建省莆田市)某市要在一块平行四边形ABCD的空地上建造一个四边形花园,要求花园所占面积是平行四边形 ABCD面积的一半,并且四边形花园的四个顶点作为出入口,要求分别在平行四边形ABCD的四条边上,请你设计两种方案:
(1)如图1-1所示,两个出入口E、F已确定,请在图1-1上画出符合要求的四边形花园,并简要说明画法;
(2)如图1-2所示,一个出入口M已确定,请在图1-2上画出符合要求的梯形花园,并简要说明画法.
【评析】题意简明,但由于四边形中两个点的不确定性,给学生带来许多遐想,关键看学生能否通过分析,联想到平行线,等底等高等面积的思路.(如下页左上图)一般来说,学生画出草图后,对动点G、H的位置分析,需建立在对平行线性质及相关知识的熟悉程度,特别是平行四边形与三角形的面积关系上.本题考查:①灵活构造平行线,运用平行线相关性质;②活用面积公式中的等底等高等面积;③平行四边形知识及平行四边形与三角形面积关系.
作法:方案(1):
画法1:
①过F作FH∥AB交AD于点H.
②在DC上任取一点G连接EF、FG、GH、HE.则四边形EFGH就是所要画的四边形(下页左上图);
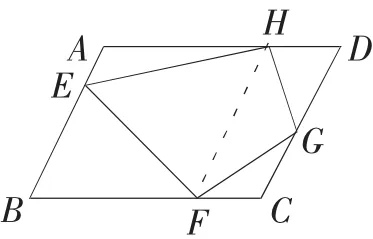
画法2:
①过F作FH∥AB交AD于点H.
②过E作EG∥AD交DC于点G,连接EF、FG、GH、HE.则四边形EFGH就是所要画的四边形(下图).

画法3:
①在AD上取一点H,使DH=CF.
②在CD上任取一点G连接EF、FG、GH、HE.则四边形EFGH就是所要画的四边形(下图).
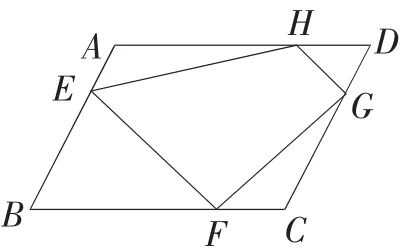
方案(2):
画法:①过M点作MP∥AB交AD于点P.
②在AB上取一点Q,连接PQ.
③过M作MN∥PQ交DC于点N,连接QM、PN、MN.则四边形QMNP就是所要画的四边形(下图).
二、在学为所用中考查实用能力——定圆覆盖定区域问题
用圆面覆盖一个特定的区域,在现代通讯设施中经常用到,如在卫星、手机信号发射塔等;这是近几年中考中出现得比较新的问题,往往会激发学生对生活环境的再认识,对所学知识的再思考.由于圆心或半径的不确定性,造成覆盖区域的大小变化,解题时需增加动态变化思考,抓住动态中的规律是试题的主要思想.
例2:(2008年江苏省无锡市)一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1)能否找到4个这样的安装点,使得这些点安装了这种转发装置后能达到预设的要求?(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用.)
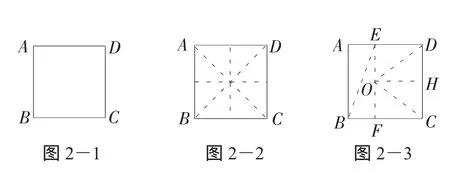
【评析】覆盖问题是圆结合其他几何知识点综合运用的另一方式,在竞赛题中出现比较多.只要关注定圆覆盖的最大、最小区域,或覆盖中的最大、最小圆半径即可解决问题,其所用到的知识也只是圆的概念、勾股定理等一些基本计算问题.思维过程不复杂,就是看能不能分析、思考到位,这是思维缜密性程度的问题.本题是一个圆覆盖正方形的问题,显然重点在于找出圆心所在位置.由题意可以得到正方形对角线长度为≈42.42<62,故对问(1),安装4个,答案有多种,如图2-2,①可先把大正方形分割成4个全等的小正方形,然后安装在4个小正方形的对角线交点上.②4个点设在大正方形各边的中点也可以.对问(2),因为>31,故一个安装点不能覆盖大正方形,可以知道一个安装点必须安在正方形一边的中垂线上,其覆盖的最大区域是一个对角线长为31km矩形,此时矩形的宽为≈7.810,显然<30,可知安装两个点也不够.如图2-3,分割大正方形,取EF中点O,当AE=时,DE=30-,OD=≈26.78<31,显然至少要安装3个才能覆盖.
三、在数学文化中考查数学思想——圆球二积的转化运算
对圆面积、球体积的公式运算,那是最为简单的问题,然而在中国数学文化中,有许多数学家在解决数学事件中运用的数学思想却是让人赞叹不绝的,这类问题激发了学生的解题热情,对学生的思想起着积极的推动作用.



四、在新定义型试题中考查新思想——旋转和相似结合思想
新定义型试题往往给出一个新概念、新名称,以运算形式、几何证明、函数等形式出现,考查学生在短时间内,以最快的速度理解、接受并运用新知识解答数学问题.新定义试题除了一般优点之外,同时还注入新的数学思想方法.一方面是体现了新定义型试题结构、命题思想日趋成熟,另一方面也是对学生知识方法的渗透.
例4:(2007年江苏省南京市)在平面内,先将1个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P'在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过放缩和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
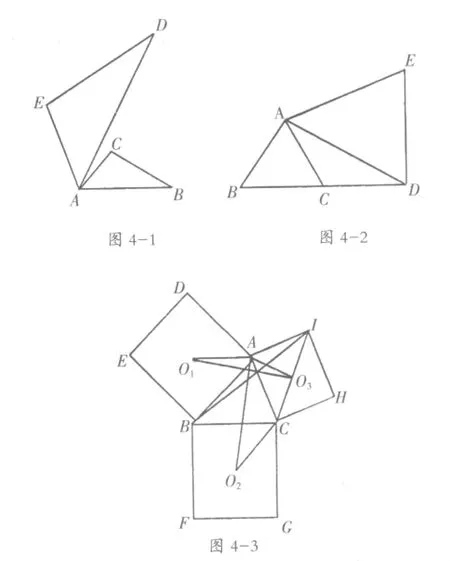
(1)填空:①如图4-1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(____,_____);
②如图4-2,△ABC是边长为1cm的等边三角形,将它作旋转相似变换A(,90°),得到△ADE,则线段BD的长为_____cm;
(2)如图4-3,分别以锐角三角形ABC的三边AB,BC,CA为边向外作正方形ADEB、BFGC、CHIA,点O1,O2,O3分别是这三个正方形的对角线交点,试分别利用△AO1O3与△ABI,△CIB与△CAO2之间的关系,运用旋转相似变换的知识说明线段O1O3与AO2之间的关系.
【评析】往常在几何推理中总是把旋转和相似分步解决.本题把旋转和相似结合起来,形成一种新的图形变换形式,对学生在几何思维方面有较大的帮助.通过(1)的简单应用,在(2)中得到升华:介绍了一种同时能证明线段相等、垂直关系的一种数学方法,用旋转相似组合变换思想,同时把相似三角形之间边之间的数量关系和角度关系同时说明,显得说理过程简洁明了,不像在平时学习中把边的数量关系和边的位置关系分开说理那样复杂,这是一种很好的说理方法,对学生来说,可以作为以后解答数学问题的一种思想方法.问(2)思路分析:因△AO1O3∽△ABI,可理解△AO1O3放大,逆时针旋转45°得到△ABI,即线段O1O3放大倍后,再逆时针旋转45°得到BI;同理可理解BI放大,再逆时针旋转45°得到AO2,因此O1O3=AO2,O1O3⊥AO2
简解:(1)①2,60°;②2.

五、在实际问题中考查尺规作图——尺规划分的奥运场馆
尺规作图主要是考查常规作图技能,有时还需要简单的几何推理作辅助,对目标图形进行作图原理分析、作图方法探索.虽然题目要求比单纯的技能操作上了一个档次,但这充分显示了尺规作图的本质含义.本例技能与推理相结合,实践应用性强,问题简明,思考角度直接,突出了尺规作图本质与实际的意义.
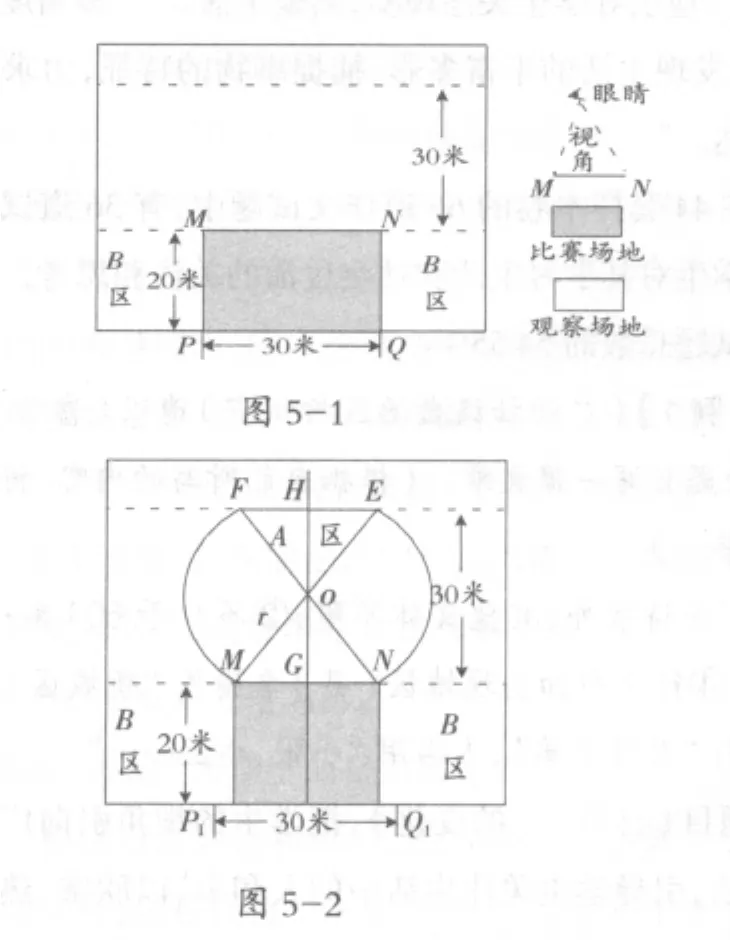
例5:(2008年浙江省丽水市)如图5-1是2008年北京奥运会某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30米的区域划分为A票区,B票区如图所示,剩下的为C票区.
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要求作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
【评析】结合了奥运场馆票区的划分、视角的特征,比单纯地说明圆周角,显得更有创意,更有实际应用价值.本题考查的只是尺规作图与圆周角概念的有效结合及简单的面积计算.
作法:(1)如图5-2,作线段MN的中垂线交MN为点G,取GO等于MG,以点O为圆心,以OM为半径画圆弧交虚线(与场地边缘MN相距30米)为点E、F,则EF与所围成的区域就是A票区.
(2)连接OM、ON、OE、OF,设MN的中垂线与EF交于H.由题意得∠MON=90°.

六、对亮点试题的新认识
1.亮点试题的价值.
让更多的人知道中考只是考查基本知识、基本技能、基本思想.中考复习时间的比例应侧重于基础知识、技能的训练,重视解题思想、解题方法的研究与运用,不必为获取高分走解难题、怪题的路.重视多变的教学方式、学习方式,让学生多多合作交流,交流多角度的思维方式、多元的解决问题方法,达到共同提高能力的目的.
2.亮点试题的来源.
试题往往来源于:学生易错的题型,师生都不太重视的“熟悉”题型,常用知识结合实际问题的换脸题型,数学方法在新环境中的运用题型,等等;而要提高学生的学习能力,特别解决问题的能力,笔者认为在抓好“三基”的同时,应培养学生良好的思维习惯,让学生学会在合作中互相编制题目考查对方,在日常生活中能从数学角度看问题、发现问题、探讨问题、解决问题.当然作为教师在关注学生的全程学习水平外,还要用不同的精制题型以及自编的新题型撞击学生的“软肋”.特别是教师自编题型往往来源于学生的平时薄弱环节,对学生的教学效果会有更好一些.
F
E-mail:hit790205@163.com
❖编辑/张烨

