切割函数的运动不变性

岳崇山

(河北北方学院理学院,河北张家口075000)

M.Brady[1]研究了平面 (或空间)区域的外形识别问题;M.Bruce,P.J.Giblin[2]和C.G.Gibson[2]则研究了外形识别中的中心对称集;而Peter J.Gibin,Donal B.O’shea[3]讨论了平面曲线的双切圆问题.本文对参考文献 [3]中定义的曲线的切割函数进行了拓广,并考察了拓广的切割函数的运动不变性.

1 基本概念

定义1.1[4]一个n阶实矩阵U叫做一个正交矩阵,如果

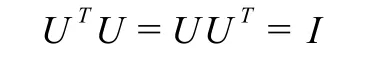
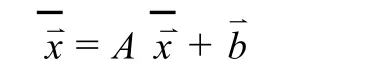
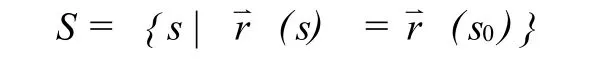
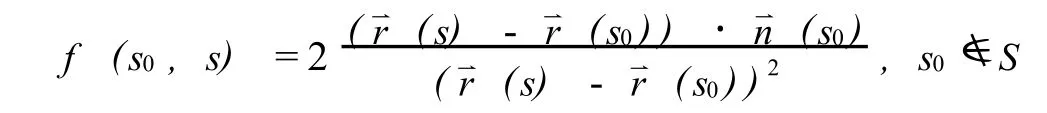
为曲线的切割函数,

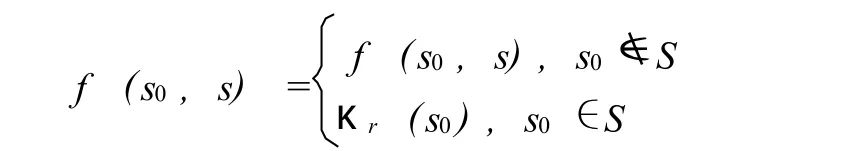
为曲线的拓广的切割函数 .

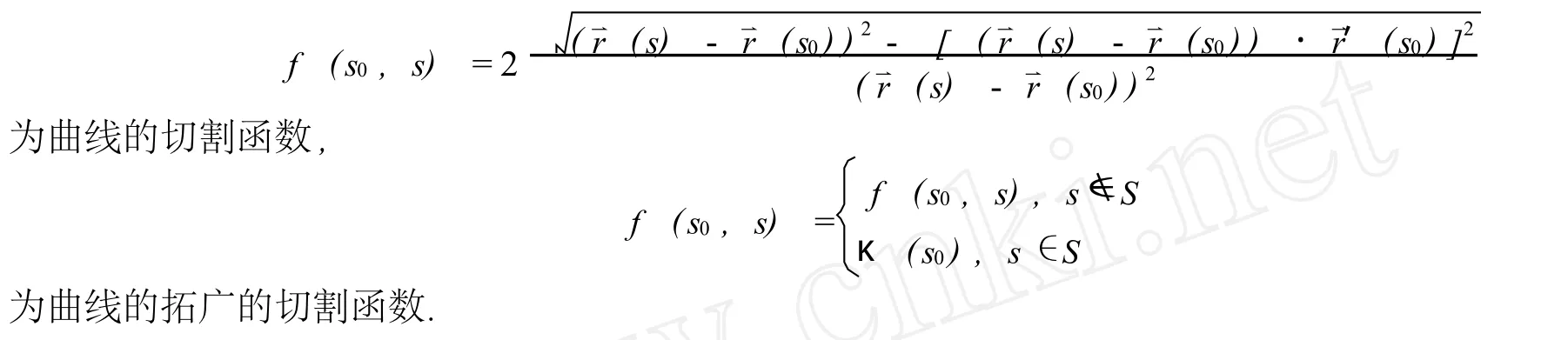
2 理论准备

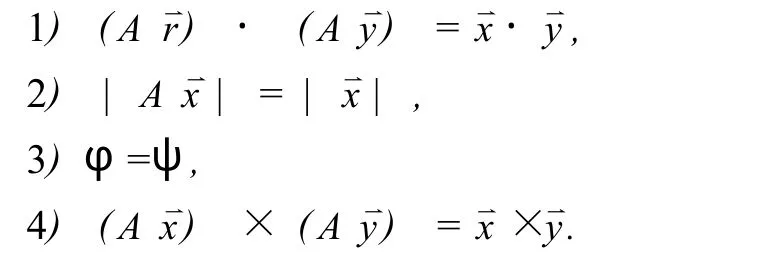
证明 1)2)3)的证明见参考文献 [4].

引理2.2 设A=(aij)是一个二阶正交矩阵,=(x1,x2),=(y1,y2)是两个二维向量(或者看成是点),令

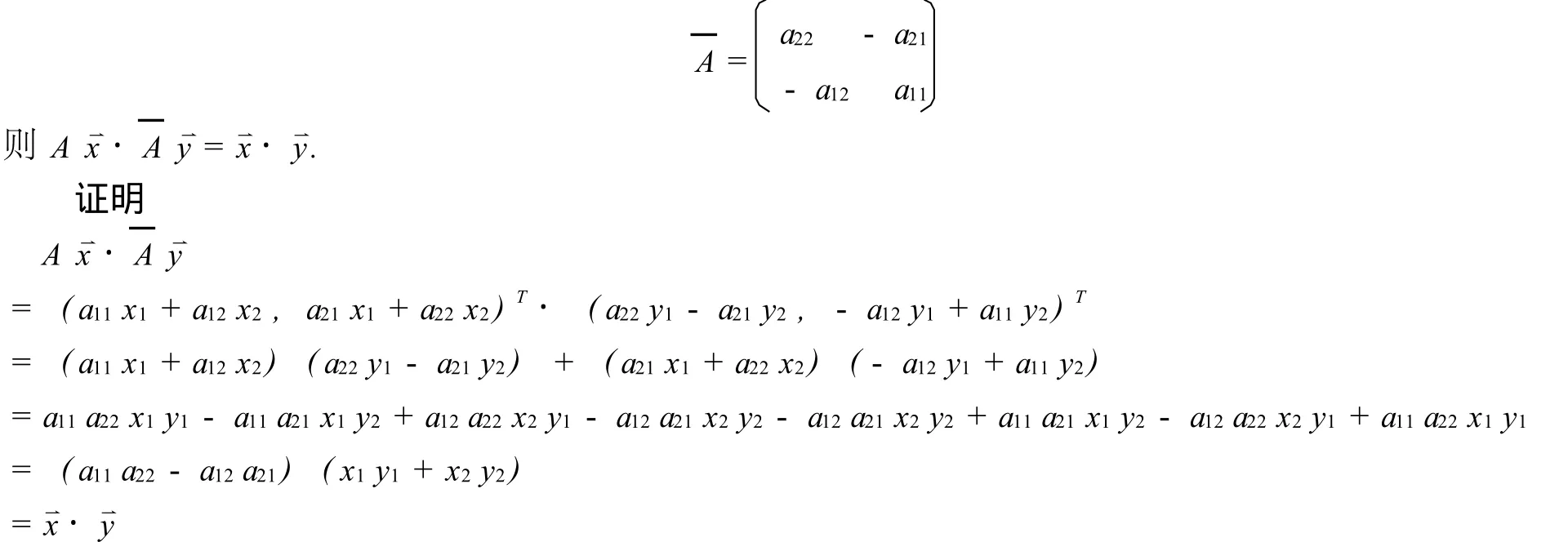
记

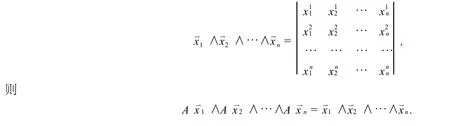
特别地,当 n等于2和3时,我们有

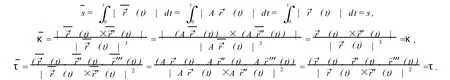
如果所给曲线是平面曲线,利用引理2.1和引理2.3,

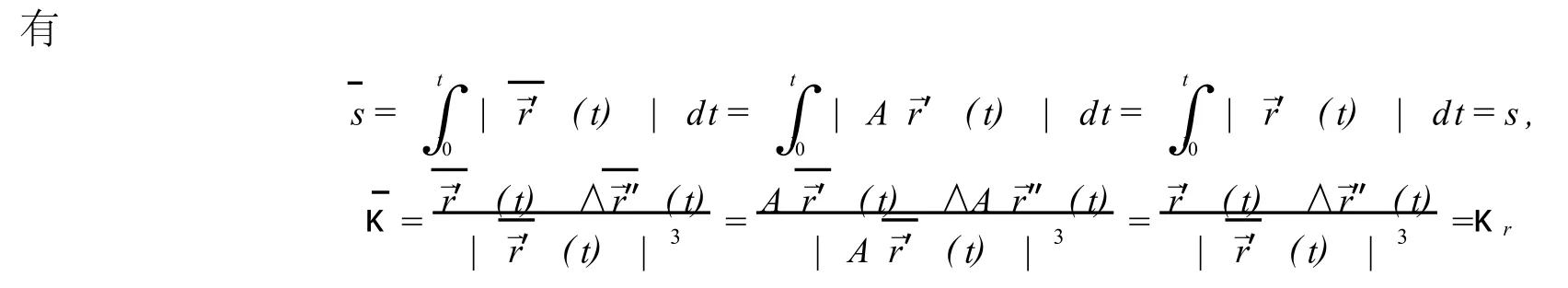
所以下面的定理成立.

定理2.1 弧长,曲率 (或相对曲率)和挠率是曲线的运动不变量.

3 主要结果

下面我们来考察平面曲线的拓广的切割函数的运动不变性.

定理3.1 平面曲线的拓广的切割函数是运动不变量.

证明 设⇀r(s)为平面曲线,(s) 经过运动

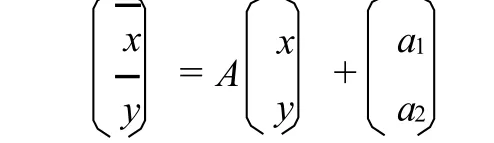
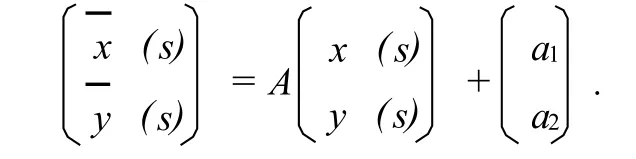
上式两边同时对s求导有

当s0∈S时,由于曲率是运动不变量,所以有(s0) =κ(s0).总之,拓广的切割函数是运动不变量.

定理2.2 空间曲线的拓广的切割函数是运动不变量.

证明 设⇀r(s)为空间曲线,(s)_经过运动

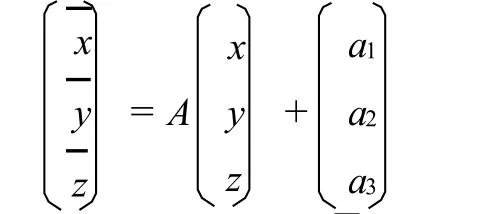
之后得到的曲线.由于弧长s为运动不变量,所以我们可设⇀r的参数也是弧长s,即(s).

从而有

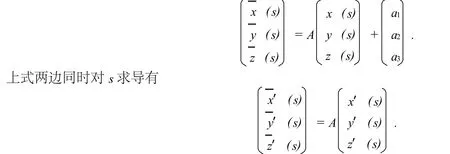
这样当s0∉S时,利用引_理2.1有

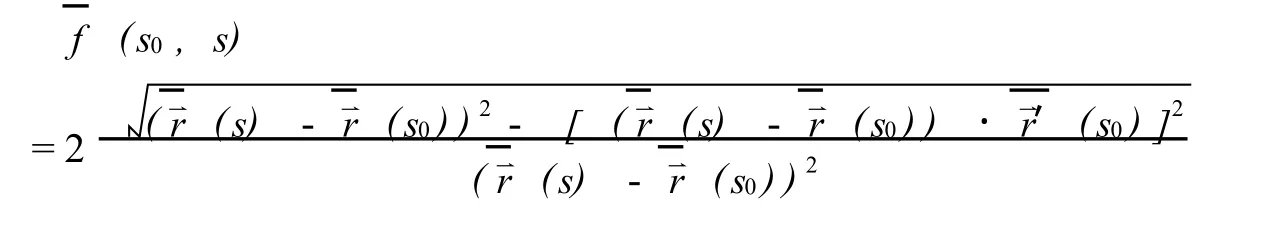
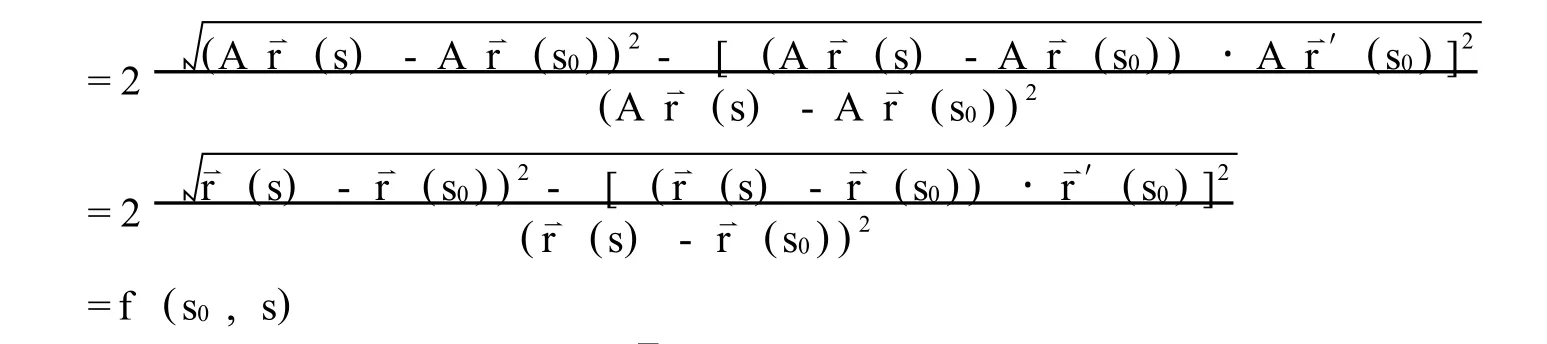
当s0∈S时,由于曲率是运动不变量,所以有(s0) =κ (s0).总之,拓广的切割函数是运动不变量.

[1] Brady M.Criteria for representations of shape[M].New York：Academic Press,1983：23-34

[2] Bruce M,Giblin PJ,Gibson CG.Symmetry set[M].Edinb：Proc Royal Soc,101A(1985)：163-186

[3] Peter J G,Donal B,O’shea.The Bitangent Sphere Problem[J].Amer Math Monthly,1990,97(01)：5-23

[4] 张禾瑞,郝鈵新.高等代数 (第四版)[M].北京：高等教育出版社,1999.334-341

[5] Duan HB.The existence of bitangent spheres[J].Edinb：Proc Roy Soc,1989,1-2,85-87

[6]John WR.Geometry of Curves[M].U.S：Chapman and Hall/CRC,1935：56-231

[7] 周兴和.高等几何 [M].北京：科学出版社,2007：106

[8] 张筑生.数学分析新讲 (第一册)[M].北京：北京大学出版社,1990：78-98

[9] 陈维桓.微分几何 [M].北京：北京大学出版社,2006：75-109

[10] 梅向明,黄敬之.微分几何 (第二版)[M].北京：高等教育出版社,2003：12