系统方程与框图的快速转换
周传璘
(孝感学院物理与电子信息工程学院,湖北孝感432000)
系统方程与框图的快速转换
周传璘
(孝感学院物理与电子信息工程学院,湖北孝感432000)
在信号与系统中,模拟方框图对于系统的建模及实现具有重要的作用,而在系统的分析中,也常常需要将实际系统的框图和方程进行相互转换。针对目前系统框图与方程之间的转换所采用的方法费时且计算量大的特点,提出了一种基于系统的线性时不变性的方程与框图的快速转换方法。实例说明:此快速转换方法简单、可行,只需要通过简单移位变换即可实现系统框图与方程的快速转换,从而省去了大量的中间数学推导过程。
方程;框图;快速转换
在信号与系统中,常需要将实际系统的框图和方程进行相互转换。对于简单的一阶系统或激励项为一项时,此过程相对简单;而对于多阶系统或激励项为多项时,转换变得比较复杂[1]。黑龙江科技学院的范艳根等[2]对常用的系统函数法和时域中间变量法进行了对比研究,发现时域中间变量法的计算量小,操作简便。北京工商大学的朱启昧[3]提出了框图到方程转换的另一种简单方法,进行对比代换完成转换过程,并无严格的数学依据。除此之外,再无文献报道简单快捷的转换方法。
基于此,笔者在多年讲授“信号与系统”课程的基础上,依据系统的线性时不变性,提出了一种快速转换方法。此方法只需要通过简单的移项变换,即可实现系统框图与方程之间的快速转换,特别是在学生没有学习变换域及信号流图时,仅仅在时域利用线性时不变性实现方程与框图的快速转换,比现有方法简单,更有利于学生理解线性时不变性及其应用。
1 系统框图到方程的转换
当框图只有一个加法器时,围绕加法器输出很快可以写出其相应的方程;而当有两个加法器时,必须建立中间变量,并设法消去中间变量,间接得到方程。
例1某连续系统框图如图1所示,试写出其微分方程。

图1 连续系统例题框图
1.1 传统方法
1)对于连续系统,选最右端积分器输出为中间变量 x(t);对于离散系统,则选最左端延迟单元输入为中间变量x(k)。以图1为例,中间变量设为x(t)。
2)写出各加法器输出信号的方程。
输入端:

输出端:
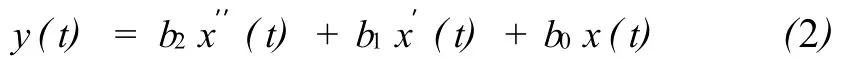
3)通过复杂代换[1-2]消除中间变量 x′′(t),x′(t),x(t),即可得到系统的方程为:

消除中间变量的过程计算量较大,数学推导多,费时费力。
1.2 快速转换法
第1)、2)步与传统方法相同。
3)巧用线性时不变性质,无须通过比较复杂的数学推导消除中间变量即可完成框图到方程的转换:
将(1)式移向整理得:

可以将(4)式看作当激励为 f(t)时的系统的响应为 x(t)。利用线性时不变性,由 b2f′′(t)+b2f′(t)+b0f(t) 引 起 的 响 应 则 为 b2x′′(t) +b1x′(t)+b0x(t),即(2) 式中的 y(t)。
(2) 式表明 y(t) 是 x′′(t),x′(t),x(t) 的线性组合,因而以 y(t)为未知变量的微分方程左端的形式应与 (4) 式相同[1],即 y′′(t)+a1y′(t)+a0y(t)=ζ(t)。即输入为ζ(t)时,系统的响应为y(t)。
结合前面的讨论,ζ(t) 应等于 b2f′′(t)+b1f′(t)+b0f(t),则可得系统的微分方程为:
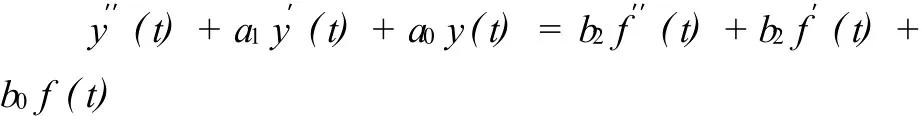
2 方程到系统框图的转换
如果方程右边只有一项,也就是说框图只有一个加法器时,则转换都非常简单;但当方程右边有两项及以上时,必须建立中间变量,通过有关的运算及代换,建立输出与中间变量的关系方可画出框图。
例2知某系统差分方程为
y(k)+a1y(k-1)+a0y(k-2)=b1f(k-1)+b0f(k),请画出该系统框图。
2.1 传统方法
文献[2]给出了两种常用的由方程转换到系统框图的方法,即系统函数法和时域中间变量法。前者需要对系统方程求拉氏变换或 Z变换以得到系统函数,再将系统分为全极点系统和全零点系统,然后分别实现其框图并级联可得到整个系统框图。后者首先引入中间变量,然后将系统依照输入、输出加法器分为两个部分,分别进行框图的实现,然后找到两个框图之间的联系,并进行合并。整体上来讲,该文献在进行系统方程到框图的转换既费时又费力,需要很多中间代换环节,很容易出错,在课堂上讲授因数学推导较多也不易被学生接受。
2.2 快速转换法
由方程可见,该系统是一个二阶系统,则需要两个延迟单元和两个加法器。
1)建立中间变量 x(k),使其满足

2)导出各个加法器的输入、输出关系。
(5)式可以理解为当激励为 f(k)时,其响应为 x(k),则利用线性时不变性,当激励为 b1f(k-1)+b0f(k)时,其响应也必然为 b1x(k-1)+b0x(k)。而例题中方程可理解为 b1f(k-1)+b0f(k)产生的响应为 y(k),则

(6)式即为输出端加法器的方程。
同时将(5)式进行移项可得输入端加法器方程:
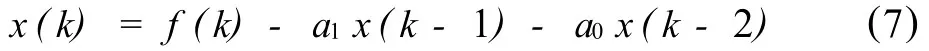
3)利用(6)式和(7)式,可迅速画出该离散系统框图,如图2所示。

图2 离散系统例题框图
3 结论
线性时不变性质是信号与系统中十分重要的性质,在信号与系统的分析中正确理解并巧妙地利用该性质往往可以收到事半功倍的效果。文中笔者根据线性时不变性完成了框图与方程之间的快速转换,对于多阶系统,特别是系统框图有多个加法器或方程右边有多项时,该方法具有明显的优越性。
[1] 吴大正,杨林耀,张永瑞.信号与线性系统分析[M].4版.北京:高等教育出版社,1998.
[2] 范艳根,王玉萍,汤旭日.系统微分方程与系统框图互换的两种方法[J].黑龙江科技学院学报,2005,15(1):47-49.
[3] 朱启昧.信号与系统中框图与方程间关系的另一种推导尝试[J].北京工商大学学报,2004,22(6):32-34.
Fast Conversion between Block D iagramsand Equations
Zhou Chuanlin
(School of Physics and Electronic Information Engineering,Xiaogan University,Xiaogan,Hubei 432000,China)
Block diagram s takes an important role in system’smodeling and realizing in signal and system s,w hile it is usually necessary to exchange between system equation and block diagram s in system analysis.At present,the common method for the conversion between system equation and block diagram s is complicated and taking much time.It is for this reason that we have proposed a method for fast conversion between equations and block diagram s based on the linear time invariant of system s.The example show s that this method is simple and available,and can savemuch more time formathematical deduction through simple changing.
equation;block diagram s;fast conversion
TN911.6
A
1671-2544(2010)03-0051-03
2010-04-02
湖北省高等学校教学研究项目(20060363)
周传璘(1965— ),男,湖北汉川人,孝感学院物理与电子信息工程学院副教授,硕士。
(责任编辑:邹礼平)

