倾斜卧式储油罐的罐容表标定
薛茴文,林智燕,王 倩,李韶伟
(台州学院 数学与信息工程学院,浙江 临海 317000)
倾斜卧式储油罐的罐容表标定
薛茴文,林智燕,王 倩,李韶伟*
(台州学院 数学与信息工程学院,浙江 临海 317000)
探讨圆形封头卧式储油罐发生纵向变位α和横向偏转β的罐容表的标定问题,建立卧式储油罐的储油量与油位高度H0及变位参数α,β的函数模型和近似模型;根据给定的一组实测数据,利用最小二乘法原理得到了变位参数α,β,进而标定了新的罐容表,并分析误差证实了模型的可靠性。
卧式储油罐;罐容表;变位参数
1 引言
无倾斜偏转的情况下,卧式储油罐的储油量与油位高度的关系[1-3]很容易得到。储油罐发生纵向变位α和横向偏转β导致原罐容表不准确,因此需要重新标定罐容表。储油罐为一规则几何体,忽略温度、气压等自然因素及油的挥发损耗等因素影响,我们建立了储油罐的储油量与油位高度及变位参数 α,β 的函数模型[4]。
2 模型的建立与求解
2.1 模型Ⅰ:无偏模型
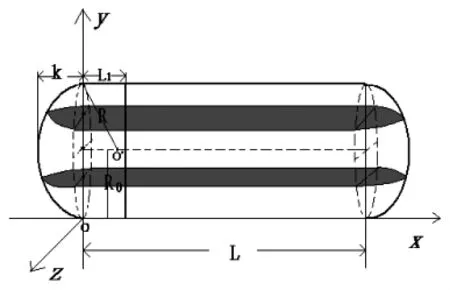
图1 无倾斜偏转时的卧式储油罐
当卧式储油罐无倾斜偏转时,如图1所示建立空间直角坐标系,则卧式储油罐的储油量模型[2]为:
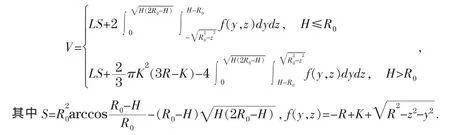
2.2 模型Ⅱ:倾斜偏转模型
卧式储油罐的现在位置是经过先横向偏转β后纵向倾斜α得到的。先考虑卧式储油罐横向偏转β,如图2所示,横向偏转β后读取的油位高度H0与无横向偏转时的油位高度H1的关系满足


图2 横向偏转截面示意图
以下从油位高度H1出发只考虑纵向倾斜。
如图3所示,以左球缺最低点为原点O,过原点O的储油罐圆柱体母线方向为x轴,垂直纸面向外方向为z轴正方向,垂直于xoz面向上方向为y轴正方向建立空间坐标系。
不同的油位高度,卧式储油罐的储油量的计算方式也不同,分5种情况讨论如下.
2.2.1 当 0≤H1≤(L-L1)tanα 时,
由图4所示,左球缺被z=z平面所截的有油部分面积为
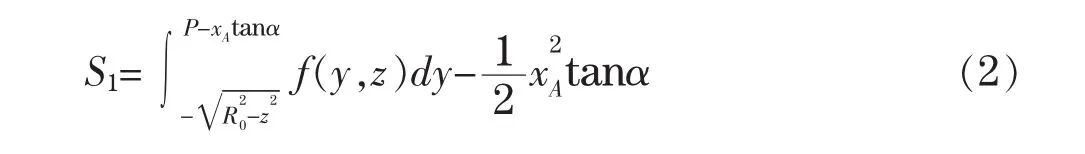
其中 P=L1tanα+H1-R0,xA为 A 点的横坐标。
则卧式储油罐的储油量为
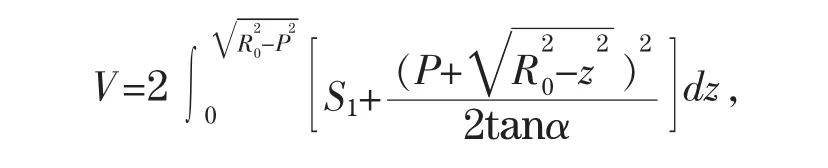
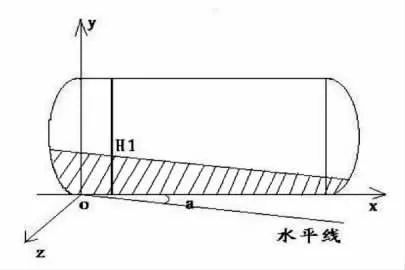
图3 倾斜卧式储油罐空间坐标系
2.2.2 当 (L-L1)tanα<H1≤R0-L1tanα 时,x=0 处的油面高度没有超过R0。
2.2.2.1 左球缺的储油量
左球缺被z=z平面所截的有油部分面积为S1,此时储油量为
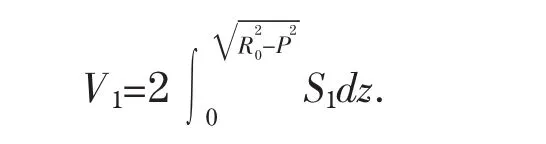
2.2.2.2 圆柱体部分的储油量
油罐圆柱体部分在x=x平面上所截的有油部分面积[2]为

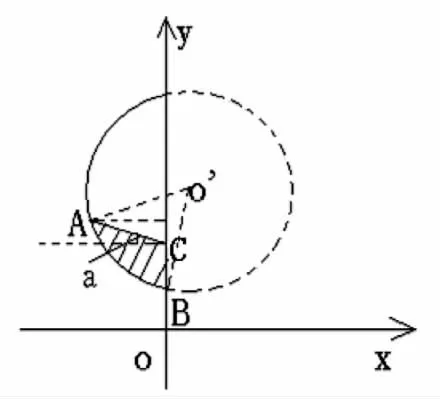
图4 左球缺的z=z截面示意图
其中 h(x)=-tan(α)(x-L1)+H1.
则圆柱体部分的储油量为

2.2.2.3 右球缺的储油量
类似于情况2.2.2.1,右球缺的储油量为

2.2.3 当 R0-L1tanα<H≤R0+(L-L1)tanα 时,
如图4所示,左球缺被z=z平面所截的无油部分面积为

则左球缺的储油量为
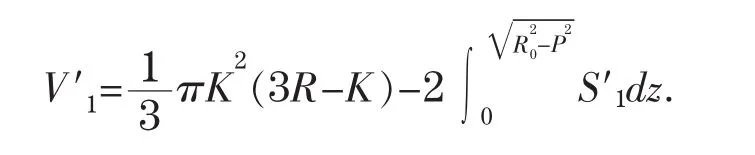
此时圆柱体和右球缺的储油量计算公式与情况2.2.2相同,也为V2和V3。
2.2.4 当 R0-(L-L1)tanα<H1≤2R0-L1tanα 时,
类似于情况2.2.3,左球缺和圆柱体的储油量也为V′1和V2。右球缺的储油量为
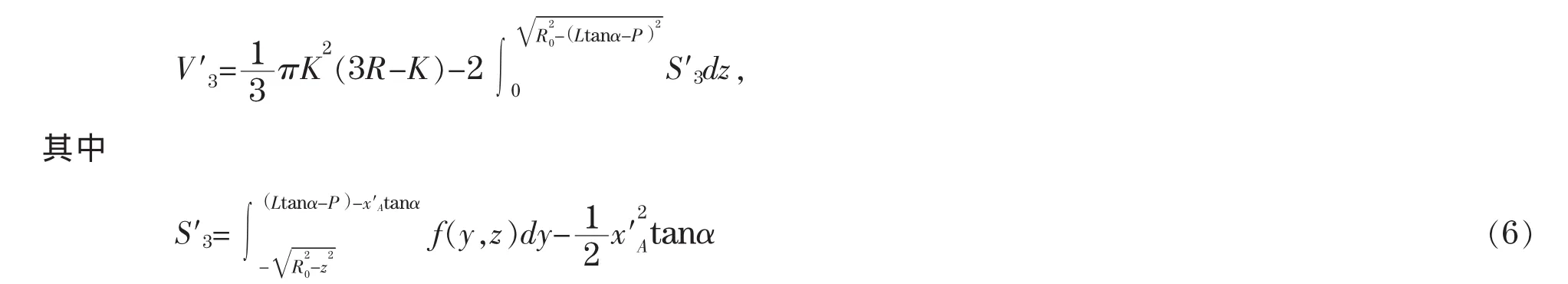
2.2.5 当 2R0-L1tanα<H1≤2R0时,
卧式储油罐的储油量为

综上所述,卧式储油罐的储油量模型为

其中 S1,V2,S3,S′1,S′3分别见(2-6)式。
2.3 模型Ⅲ:近似模型
由于模型Ⅱ中的xA和x′A表示形式很复杂,导致模型的积分难以求解,从而很难得到变位参数α和β。因此我们需要建立了一个易求解的近似模型。
如图5所示,将左球缺内的倾斜油面以平面y=yC来替换(右球缺类似处理)。消除上述A和A’点的计算难点,进而得到模型Ⅱ的储油罐的近似模型如下:
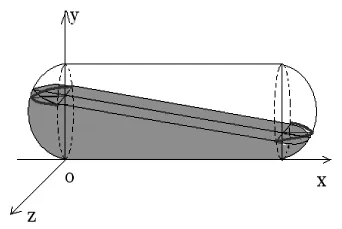
图5 卧式储油罐的近似示意图

其中 V2见(3)式。
2.4 模型Ⅲ的求解
根据2010年全国大学生数学建模竞赛A题给定的L=8,L1=2,K=1,R0=1.5,R=1.625和附件2中的实测数据(第i次测量得到的油面高度hi及出油量△i),可得油面高度hi对应的储油量

为得到变位参数α,β及初始油量V0,根据最小二乘法原理[5]
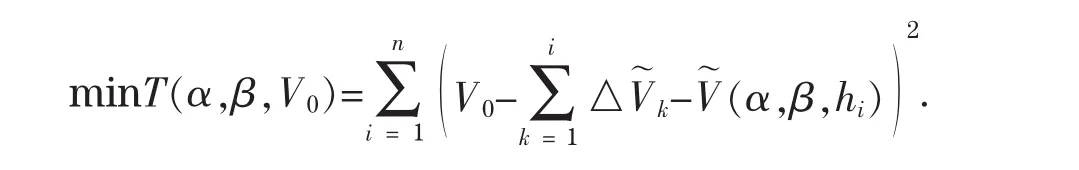
利用 Matlab 软件可编程[6]搜索得到 α≈2.090,β≈4.240。
2.5 罐容表的标定
根据卧式储油罐的模型Ⅰ(无偏转时储油量V=V(H))和模型Ⅲ(倾斜偏转后储油量V≈(α,β,H0))及所求得的α≈2.090,β≈4.240,分别得到罐容表(见表1及表2)。
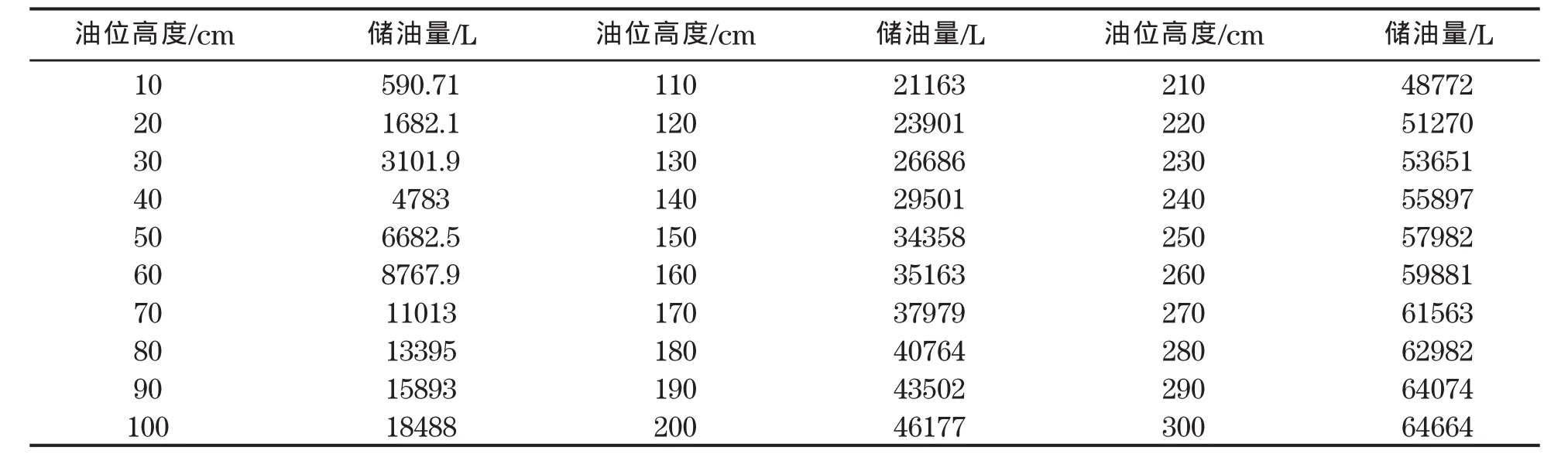
表1 无偏转时卧式储油罐的罐容表
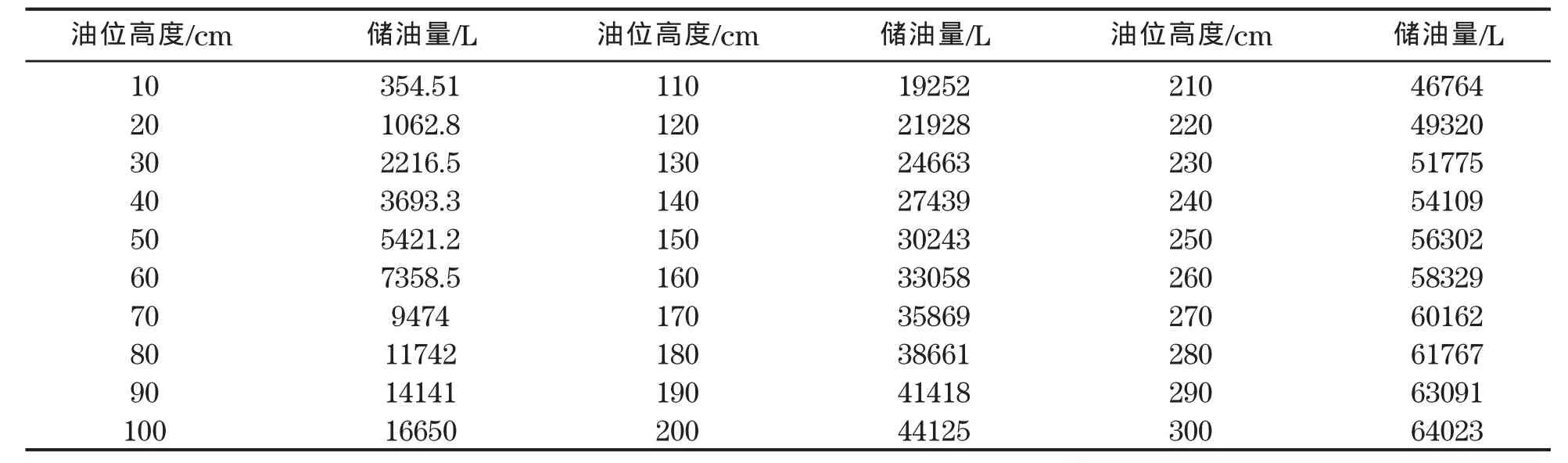
表2 倾斜偏转卧式储油罐的罐容表
2.6 结果分析
(1)根据给定的L,L1,K,R,R0和附件 2 油面高度hi及储油量Vi的数据,可比对得到模型Ⅰ的计算误差[6]。如图6所示模型Ⅰ与实验数据完全契合。

(3)当(L-L1)tanα<H1≤2R0-L1tanα 时,模型Ⅲ的计算误差为
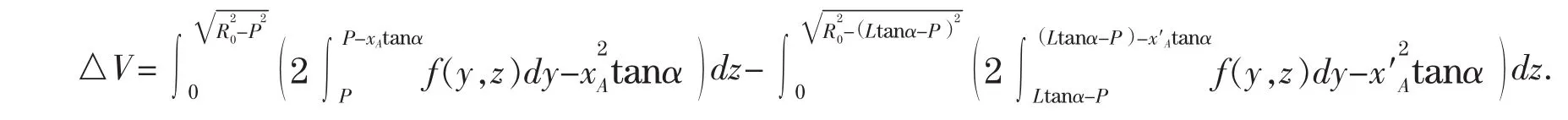

图6 模型Ⅰ的结果
实际上,储油罐的变位参数α和β都很小,此时tanα≈α,cosβ≈1,△V≈0模型Ⅲ可行且有效。
在此,特别感谢李韶伟老师对论文的悉心指导!
[1]刘奇央.卧式容器容积与液位的关系式[J].黑龙江电力技术,1998,20(4):215-217.
[2]田铁军.倾斜卧式罐直圆筒部分的容积计算[J].现代计量测试,1999(5):32-36.
[3]宁苗苗.液氨储存罐深度——容积函数的建立与应用[J].高等函授学报,2010,23(1):73-74.
[4]姜启源,谢金星,叶俊.数学模型(第三版)[M].北京:高等教育出版社,2003:82.
[5]钱政,王中宇,刘桂礼.测试误差分析与数据处理[M].北京:北京航空航天大学出版社,2008:110.
[6]刘同娟,郭建,刘军.Matlab 建模、仿真及应用[M].北京:中国电力出版社,2009:31.
The Tank Capacity Table Horizontal Calibration Tank
XUE Hui-wen,LIN Zhi-yan,WANG Qian,LI Shao-wei
(School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China)
This paper discusses the occurrence of circular tank head horizontal deflection and vertical deflection of the tank capacity table horizontal calibration problem. It establishes the amount of horizontal storage tanks and oil storage height,and deflection function model parameters and approximate model.Based on a given set of measured data,modification parameters are obtained by using least squares method,the new tank capacity table is calibrated,and the reliability of the model is proved by analyzing its error.
horizontal storage tank;tank capacity table;modification parameters
耿继祥)
TB938.8
A
1672-3708(2010)06-0004-05
2010-11-05;
2010-12-01
李韶伟(1979- ),男,浙江仙居人,讲师,博士生,主要从事偏微分方程方面的研究。

