多体GHZ态的远程制备
金丽丽,梁华秋,朱莎莎,倪娇霞
(台州学院 物理与电子工程学院,浙江 台州 318000)
多体GHZ态的远程制备
金丽丽,梁华秋⋆,朱莎莎,倪娇霞
(台州学院 物理与电子工程学院,浙江 台州 318000)
提出了两种制备多体GHZ态的方案。为了改造量子信道,在两个方案中,均使用了一个辅助粒子。第一种方案,利用辅助粒子将量子信道制备到与所要制备的态相适应的参数上;而在第二种方案中,先利用辅助粒子将量子信道改造成最大纠缠态,然后再制备所需要的量子态。研究表明,两种方案所需的经典信息相同,均为1个比特,在相同的条件下,第一种方案具有较高的成功概率。
远程态制备;多体GHZ态,部分纠缠信道,辅助粒子
1 引言
量子纠缠是存在于子系统中的一种非常神奇的现象,即对一个子系统的测量结果无法独立于对其他子系统的测量参数[1],它是量子力学中特有的现象。基于量子纠缠这一神奇特性,人们提出了量子隐形传态[2]方案,发送者Alice向远处的接收者Bob传送一个对于两者都未知的量子态,而发送者原来所拥有的量子态在此过程中将被破坏。若干年后,由 Lo[3]、Pati[4]和 Bennett[5]等人又提出了传送量子态的另一方案——远程态制备方案,在此方案中,发送者完全知道所要传送的量子态的全部信息而接收者对此却一无所知。量子隐形传态[2]和远程态制备[3-5]是量子通信的两种典型方案,由于远程态制备在所消耗的纠缠资源与经典信息之间存在着折衷,而且每传送一个比特的量子态所消耗的总资源(经典信息与纠缠资源的总和)较少,因此,远程态制备在量子通信领域有着十分广阔的应用前景。目前,人们对远程态制备进行了广泛而深入的研究,并提出了大量的远程态制备方案[6-9],例如高维空间的远程态制备[6,7],低纠缠远程态制备[8],对混合态的远程制备[9]。目前,人们在理论和实验上进一步探讨如何在物理系统中实现量子信息的传送,并已取得了许多有价值的成果,例如人们利用腔量子电动力学技术实现远程态制备[10,11]。远程态制备在实验上也取得很大的进展,线偏振光学元件[12,13]和核磁共振技术[14]被广泛用来实现远程态制备。
在远程态制备过程中,最大纠缠态作为量子信道无凝是人们最理想的选择,许多基于以最大纠缠态作为量子信道的远程态制备的方案被提出,例如,Pati[4]等提出利用最大纠缠EPR态来远程制备单比特态;Liu[7]等提出以两个最大纠缠EPR态作为量子信道来实现远程态制备双比特纠缠态方案;Shi[15]等提出了利用三粒子GHZ态远程制备两粒子的纠缠态和单比特态。事实上,部分纠缠态也是量子通信的重要资源,可以作为传递量子信息的信道,近来,以部分纠缠态作为量子信道的远程态制备也得到了广泛的研究,许多基于部分纠缠态的远程态制备方案不断地被提出。Mei[16]等讨论了利用部分纠缠态来远程制备单比特量子态,在接收者知道所传输量子态部分信息的情况下消耗最小的经典信息而达到高保真度。Liu等[7]在利用部分纠缠态制备两体纠缠态时,通过引入辅助粒子和适用当的酉变换,得到初态。多体纠缠态在量子通信中起着十分重要的作用,因而多体纠缠态的制备在量子通信中也是十分重要的课题。本文提出两种以N+1体部分纠缠GHZ态作为量子信道,在辅助粒子的帮助下,制备N体GHZ纠缠态,方案比较简单,具有一定的价值。
2 两种多体GHZ态的远程制备的方案
2.1 方案一
本方案首先利用辅助粒子将量子信道转变到与要制备的态具有相一致的参数上,然后再进行远程态制备。
假设Alice想要帮助Bob建立的多体部分纠缠GHZ态为

其中 θ和 φ 为实数,且 θ∈[0,π ]和 φ∈[0,2 π ]。他们共享的由N+1个粒子所组成的多体部分纠缠GHZ态为(2)
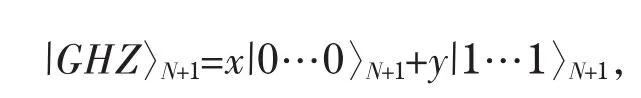

Alice对粒子1、N+2作如下变换

接着Alice使用基矢{/0〉,/1〉}对辅助粒子N+2执行正交测量,若测得结果为/0〉N+2,量子信道将转变成为

成功概率为:p1=u2。
接下来Alice对粒子1执行如下酉变换

变换后量子信道变为

然后Alice对粒子1执行Hadamard操作

接着Alice以计算基{/0〉,/1}〉为基矢对粒子1作投影测量:
①若 Alice的测量结果为/0〉1,Bob处的粒子 2,3,…,N+1将坍缩为

②若 Alice的测量结果为/1〉1,Bob处的粒子 2,3,…,N+1将坍缩为

Bob对粒子2,3,…,N+1中的其中一个作σz操作即得

由此可见,无论Alice得到的测量结果为/0〉1还是/1〉1,Bob总能得到初态:
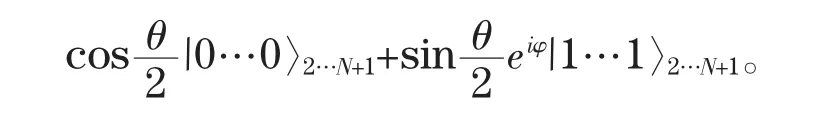
在这一方案中,所消耗的经典信息为1个比特,总的成功概率为p=u2。当u=v=1时,即量子信道与所要制备的态参数相一致时,成功概率可达到100%。
2.2 方案二
在这一方案中,首先利用辅助粒子将量子信道转变成量大纠缠信道,然后再以最大纠缠量子信道执行远程态制备。
步骤1:利用辅助粒子,将量子信道转变成最大纠缠信道。


Alice对粒子1、N+2作如下变换
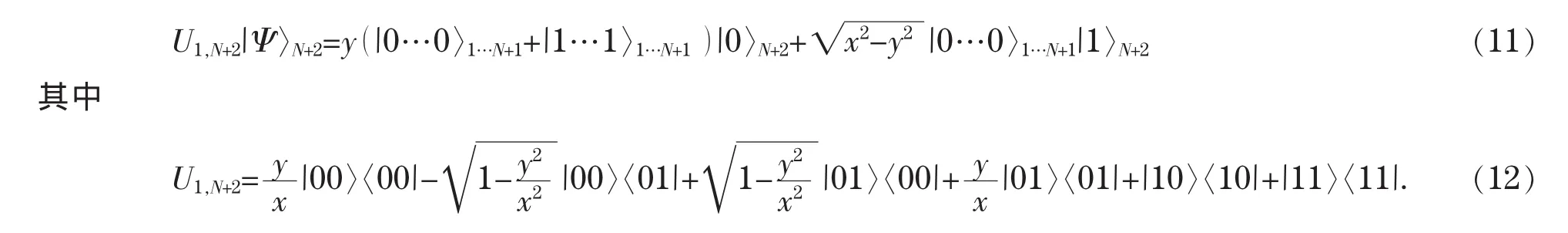
接着Alice使用基矢{/0〉,/1}〉对辅助粒子N+2执行正交测量,若测得结果为/0〉N+2,量子信道将转变成为最大纠缠信道

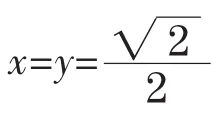
文献[15]对此已有详细的报道,其成功的概率为50%,消耗的经典信息也为1比特。

3 结论
远程态制备是量子通信的重要方案之一。一般地,最大纠缠信道可以直接用来实现完美的远程态制备,而部分纠缠态也是量子通信的重要资源,可作为量子信道来实施远程态制备。本文提出两种在辅助粒子的配合下实施远程制备多体纠缠GHZ态的方案,通过比较,我们发现两种方案所需的经典信息相同,均为1个比特,在相同的条件下,第一种方案具有较高的成功概率,当所要制备的量子态与量子信道具有相同的参数时,成功概率可达到100%。
[1]Einstein A,Podolsky B,and N.Rosen,Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? [J].Phys.Rev.,1935,47:777-780.
[2]Bennett C H,Brassard G,Crépeau C,Jozsa R,Peres A,and Wootters W K,Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels[J].Phys.Rev.Lett.,1993,70:1895-1899.
[3]Lo H K,Classical-communication cost in distributed quantum-information processing:A generalization of quantum-communication complexity[J].Phys.Rev.A,2000,62:012313-012320.
[4]Pati A K,Minimum classical bit for remote preparation and measurement of a qubit[J].Phys.Rev.A,2000,63:014302-014305.
[5]Bennett C H,DiVincenzo D P,Shor P W,Smolin J A,Terhal B M,and Wootters W K,Remote state preparation[J].Phys.Rev.Lett.2001,87,077902-077906.
[6]Zeng B,and Zhang P,Remote-state preparation in higher dimension and the parallelizable manifold Sn-1[J].Phys.Rev.A,2002,65 :022316-022320.
[7]Liu J M,and Wang Y Z,Remote preparation of a two-particle entangled state,Phys.Lett.A 2003,316:159-167.
[8]Devetak I,and Berger T,Low-entanglement remote state preparation[J].Phys.Rev.Lett.,2001,87:057901-057905.
[9]Berry D W,and Sanders B C,Optimal remote state preparation[J].Phys.Rev.Lett.,2003,90:057901-057905.
[10]Deng L,Chen A X,Xu Y Q,High efficient scheme for remote state preparation with cavity QED [J]. Chin.Phys.B,2008,17:3725-3728.
[11]Wang X W,Pen Z H,Scheme for implementing perfect remote state preparation with W-class state in cavity QED[J].Chin.Phys.B,2008,17:2346-2351.
[12]Xiang G Y,Li J,Yu B,and Guo G C,Remote preparation of mixed states via noisy entanglement[J].Phys.Rev.A,2005,72:012315-012321.
[13]Kang Y,Cho K,Noh J,Vitullo D L P,Leary C,Raymer M G,Remote preparation of complex spatial states of single photons and verification by two-photon coincidence experiment[J].Opt.Exp.,2010,18:1217-1233.
[14]Peng X H,Zhu X W,Fang X M,Feng M,Liu M L,and Gao K L,Experimental implementation of remote state preparation by nuclear magnetic resonance[J].Phys.Lett.A,2003,306:271-276.
[15]Shi B S,and Tomita A,Remote state preparation of an entangled state[J].J.Opt.B:Quantum Semiclass.Opt.2002,4:380-382.
[16]Mei Y X,Chen L,Chen Y X,Remote state preparation using non-maximally entangled state:Universality and necessary amount of quantum channels[J].Chin.Phys.Lett.,2006,23:548-551.
Remote Preparation of Multi-particle GHZ-class State
JIN Li-li,LIANG Hua-qiu*,ZHU Sha-sha,NI Jiao-xia
(School of Physics&Electronics Engineering,Taizhou University,Taizhou 318000,China)
In this paper,we investigate two protocols of remote preparation of multipartite GHZ state.In order to promote the quantum channel,we introduce an auxiliary particle in both protocols.In the first protocol,with the aid of the auxiliary particle, the quantum parameter is changed to be the most suitable to the state to be remotely prepared, and then the RSP protocol is achieved. In the second protocol, the quantum is firstly changed into the maximally entanglement, and then the RSP is implemented. Our result shows that one bit classical communication cost is enough in both two protocols respectively, and the first RSP protocol is more likely to be achieved than the second one.
remote state preparation;multi-particle GHZ-class state;partially entangled channel;auxiliary particle.
周小莉)
TB332
A
1672-3708(2010)06-0017-05
2010-10-07
浙江省教育厅科研项目(项目编号:Y200803630)
梁华秋(1967- ),男,浙江临海人,副教授,主要从事量子信息研究。

