基于分类思想的高密度数据去噪方法研究

周竹生,杨 俊,黄 平,马 阳

(1.中南大学 信息物理工程学院,湖南长沙 410083;2.中国石油西南油气田公司 勘探开发研究院,四川成都 610051)

0 前言

高密度电阻率法是八十年代国际上兴起的一种电法勘探的变种,其基本原理与常规的电阻率法完全相同。因此,它仍是以岩矿石的电性差异为基础的一类勘探方法,研究的是在施加电场的作用下,地层中传导电流的分布规律。它的电极布设是一次完成的,实现了数据采集收录自动化,智能化。因此,可以方便地采集到大量的数据,从而可以提供较为丰富的地电结构状态和地质信息,并且避免了人工操作带来的误差。

但是,在实际高密度电阻率法测量中,由于地质地球物理条件是十分复杂,地表电性不均匀,地形起伏及电极接触不好或存在其它方面的干扰等原因,都将使视电阻率结构变得十分复杂,常常使数据断面出现一些虚假点或突变点,进而造成电阻率拟断面图的虚假异常,难于对其进行准确解释。尤其是当野外条件不允许,无法改善电极接地条件时,那么只能先将数据记录下来,然后再剔除掉断面记录中的虚假数据。作者在本文中借鉴图像去噪的方法,并结合现场情况对视电阻率进行分析处理,尽可能的分辨和消除一些干扰因素的影响,最大程度地恢复了原始数据的有效性。

1 噪点分类[7]

参照图像去噪的方法,将高密度数据中的噪声点分成二个大类:①受电极接触不好或仪器供电不良造成的脉冲型噪声;②受其它地电干扰或随机干扰造成的高斯型噪声。其中又将脉冲型噪声分成绝对脉冲噪声和相对脉冲噪声。

1.1 脉冲型噪声点

对于高密度数据断面的某个区域来说,脉冲噪声会造成中心点电阻率值与周围点电阻率值之间有较大差异。对于一个实际数据资料,理想的脉冲噪声点是电阻率表现为极大值或者为负值的数据点。但是由于高斯噪声的叠加,导致脉冲噪声点的电阻率值有一定范围的改变,因此又把脉冲噪声分为二种,并分别进行判别。

(1)准理想脉冲噪点。对于电阻率值小于0,或者大于预设定阀值H的数据点,由于它接近于理想脉冲噪点,故称准理想脉冲噪点。这个阀值可以通过做数据直方图,找出数据点开始离散分布的高值点的电阻率值作为阀值,在后面噪点判别中会有说明。

(2)相对脉冲噪声点。这类噪声点的特点是电阻率值在0到阀值H之间,但相比于周围临近的其它数据点来看,电阻率值偏大或偏小,也可以认为此数据点为孤立数据点,可称为相对脉冲噪声点。

1.2 高斯型噪声点

所谓高斯噪声,是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。作者在本文所要研究的是具有高方差的高斯噪声,它的存在会使数据跳动严重,使反演结果变得不可靠。

2 噪声检测与剔除方法

为了准确地剔除噪声数据点,避免有用的数据被误剔除,作者在仔细分析了各种噪声特性的基础上,对每一种噪声提出了相应的检测方法,并给出对应的最适合的去除方法。尽力做到了在剔除噪声点的同时,保留数据更多有用的信息。

2.1 绝对脉冲噪声点的检测与剔除

在高密度电法数据资料中,脉冲噪声点总是出现在电阻率极大值区域里,或者地球物理允许的边界条件外,在电法勘探中就是电阻率为负值区域,且与高斯噪声点相比脉冲噪声点较为分散,多以孤立点出现,与周围非噪声点的电阻率差值较大。这样就可以设置高阻阀值H,把电阻率值大于H的数据点归入集合H里面。由于一次测量得到的高密度电法数据大多数分布一定的电阻率范围内,所以阀值H的确定可以通过对数据做直方图,选取数据点个数变得稀少且开始出现离散分布的电阻率值作为H;然后再把电阻率值小于零的点归入集合L,用集合M代表脉冲噪点。

显然,M⊂(L∪H)。也就是说,脉冲噪声点电阻率值一定是大于H或者小于0,但电阻率值大于H或者小于0的点并不一定是脉冲噪声点。这样就将脉冲噪声点的检测从整个数据集缩小到了集合L∪H。再根据电阻率值不能为负值这一物理限制,可以得出集合L中的点必为噪声点。这样首先就应该剔除负值点,避免它的影响通过滤波作用传递到其它数据点。

对于集合L中的点,采用传统的中值滤波方法去除。根据高密度数据点的分布特点,选取该类噪声点周围六个方向上距离该点最近的数据点,组成滤波集合(见图1)。对于选取的数据,首先判断它的值是否小于零,小于零的点就舍去,不加入滤波集合。对于边界上的点,还是按这些位置去选取数据,若位置超出数据边界,就不作选取。最后用选取数据集的中值来代替原来噪声点的值。

图1 数据点的选取Fig.1 Data point selection

而对于集合H中的点,就需要判断它是否为真正的绝对脉冲噪点。对于这类点的检测,是整个去噪过程的最为关键的一步,其成败决定了是否能成功将虚假异常点剔除,或者将真正的数据异常点误剔除掉。

标准中值滤波的滤波窗口设计,一直存在着噪声抑止与细节保护这个矛盾,作者在本文综合考虑了大的滤波窗口对噪声抑止好的优势,以及小的滤波窗口对细节保护好的优势,设计了一种新的滤波窗口。在总结图像去噪各种方法的基础上,作者设计出了带自适应的改进中值滤波算法来检测和去除该类噪声点。

由于集合H中的点都满足电阻率值大于阀值H,还需要判断的就是它是否真正“孤立”。这样,在检测噪声时,先从相对“宏观”的大窗口来观察集合H中的数据点(数据点选取见图2)统计在中心点周围六个方向上,当最内层上和次内层上的数据点电阻率大于H的个数时,计数为n。当n大于等于内层上数据点个数时,就可以排除该中心点为脉冲噪点;反之,就可以认为中心点是“孤立”的。

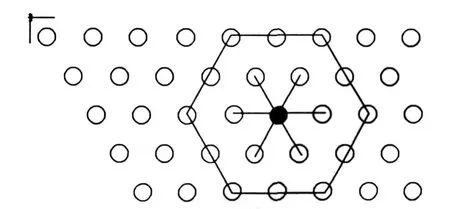
图2 改进中值滤波算法数据点选取Fig.2 Improved median filtering data point selection

对于判断为脉冲噪点的中心点,首先在内层数据点中选取满足R(i,j)

2.2 相对脉冲噪点的检测与剔除

对于电阻率值没有大于阀值H的数据点,但它与周围数据点的差值都比较大,都大于某个阀值T,这样的点就可以看成相对孤立点,也就是相对脉冲噪声点。阀值T的大小,应该根据该数据区域电阻率期望值E(R)来确定。

对于满足上述条件的点,都可以看成是相对脉冲点,不用再考虑其它条件。而对于这类噪点的滤除,采用传统的中值滤波,数据点集选取方法同去负值时一样,由于前面已经消除了绝对脉冲噪声点的影响,周围的数据点就可以全部选取到滤波集合里面,然后对这个集合求取中值来取代原来中心点上的数据。

2.3 高斯噪声点的检测与剔除

由于作者在本文中要处理的是具有高方差特征的高斯噪声,因此可以使用方差V来检验某块区域数据是否受高斯噪声严重污染。首先,将每个数据点和它们周围临近数据点组成的数据样本的方差,存在一个矩阵VAR中,这些周围数据点选取的方法同去负值时一样。用阀值V来确定方差是否过大,其中V分别取mean(VAR)、2＊mean(VAR)、4＊mean(VAR),再建立一个矩阵F。如果VAR>V,则F(i)=1;反之F(i)=0。实验证明,V的取值应该介于某个范围内。

V=(1+r)＊mean(VAR) (0

3 实验及结果分析

本次试验数据采用中、缅油气管道工程缅甸境内南塘河隧道高密度测量数据。数据采集选用的仪器是重庆奔腾数控研究所最新研制的WDJD-3高密度电法测量系统。由于野外施工条件极其恶劣,加上与当地民工语言不通,所以野外采集数据质量没办法进一步提高,只有通过室内数据去噪处理,来提高数据质量。

数据处理流程如图3所示。对每一步处理后的数据都进行了反演处理,以便对比数据,检查噪声滤除效果。

(1)在处理过程中,首先去除负值,在负值去除以后,通过作数据直方图[8](见下页图4(a))来确定去噪阀值H。在对数据做一次脉冲噪声去除后,可以通过直方图分析发现,高于阀值H的数据点都已剔除(见下页图4(b))。但从直方图还发现,电阻率值高于20 000的数据点数也很少,为验证其存在的合理性,在取H=20 000做第二次脉冲噪声去除,结果发现处理后数据变化不大(见下页图4(b)、图4(c)),说明其存在是合理的。

(2)接下来进行相对噪声去除,从三维视电阻率图上可以发现,处理后区域1的数据明显平滑了(见下页图5)。然后进行对高斯噪声点的去除,从处理前、后的视电阻率反演图上进行对比发现,数据基本上没有什么变化(见下页图6)。

图3 数据处理流程Fig.3 Data processing flow

图4 高阻去除前、后电阻率分布直方图Fig.4 Resistivity distribution histogram before and after high-resistance data point eliminated

(3)最后将各个步骤得到的数据进行反演成图(见下页图7),可以发现在以阀值30 000对数据进行处理后,反演图像已经没有什么大的变化了,这里主要的变化就是图7上最高电阻率值与最低电阻率值的差值在缩小,这是由于对数据平滑导致的,这样也增加了反演结果的可靠性。

4 结论

图5 去除相对脉冲噪声前、后三维视电阻率分布图Fig.5 Three dimensional apparent resistivity distribution map before and after eliminating relative impulse noise

图6 去除高斯噪声后三维视电阻率分布图Fig.6 Three dimensional apparent resistivity distribution map after eliminating gauss noise

高密度数据去噪的核心部份是脉冲噪声的去除。从处理数据的实例来看,当阀值H设为30 000时,由于数据点确实比较分散,程序将它们全部剔除,用改进算法的中值代替。但当第二次将阀值设为20 000时,只有很少数点被剔除了,这说明了算法并非盲目的剔除大于阀值的数据,而是对它是否真正为孤立点做出正确判断后才会进行剔除,从而验证了算法的有效性。后面相对脉冲噪声去除和高斯噪声去除后的数据已经无明显实质性变化,只是对数据做了修饰性处理。但是,在数据变化剧烈时,它可以使电阻率的变化变得相对平缓,增加反演结果的可靠性。

图7 各类噪声数据点去除后的反演图Fig.7 Inversion results after each kind of noise data points eliminated

[1] 关新平,赵立兴,唐英干.图像去噪混合滤波方法[J].中国图像图形学报,2005,10(3):332.

[2] 邹艳碧,高鹰.自适应滤波算法综述[J].广州大学学报(自然科学版),2002,(3):251.

[3] 许卫全,张新楼,徐中佑.保持图像细节的局部自适应去噪滤波器新方法[J].信号处理,2005,21(2):191.

[4] 王建华,王春平,贾洪涛.自适应中值滤波器在图像降噪技术中的应用[J].测控技术,2004,(5):54.

[5] 胡浩,王明照,杨杰.自适应模糊加权均值滤波器[J].系统工程与电子技术,2002,24(2):15.

[6] 于晓晶.中值滤波器在图像去噪中的应用[J].电脑知识与技术,2008,(9):1795.

[7] 康泱,严国萍,潘睛.基于象素分类思想的自适应图像去噪算法[J].计算机与数字工程,2006,10(4):18.

[8] 王保平,范九伦,谢维信,等.基于直方图的自适应高斯噪声滤波器[J].系统工程与电子技术,2004,26(1):1.