地震纹理属性在JJD工区断层识别中的应用

崔世凌,张军华,王 伟,谭明友,陈海云

(1.中国科学院 广州地球化学研究所,广州 510640;2.中国石化胜利油田物探研究院,东营 257022;3.中国石油大学 资源信息学院,东营 257061;4.东方地球物理公司研究院,涿州 072751)

0 前言

纹理(Texture)是按一定规则进行排列所形成的重复模式,或以一定的形式变化而产生的图案[1～4]。在自然界中,许多植物、动物、矿物,都有其独特的纹理特征。利用它,人们可以方便地识别或区分事物。在图像处理领域,利用纹理分析,可以在图像分割,模式识别,形状分析,纹理合成和图像压缩等方面得到广泛应用。

地层由于受构造运动的影响,也会产生断层、裂缝等地质现象,从而留下地质年代变迁的印记。这些痕迹,从图形学上来说,可以认为它们就是纹理,可以借助于图像处理的方法、手段,来凸显其内部特征,从而有效地识别断层或裂缝,为找油、找气提供更好的依据[5～7]。

在过去的勘探历程中,地球物理工作者通过不断努力,已经用三维地震勘探技术较好地查明落差和断距较大的断层。而对于落差和断距较小的断层识别,无论在理论上还是在实践上,都有很大困难。相干体算法也是从Bahorich和Far mer[8]的第一代的互相关算法,发展到Marfurt[9、10]的第二代多道相似算法和第三代特征值相干算法。近几年来,以Gao Dengliang[11～13]为首的研究小组,利用纹理属性进行断层识别研究,并取得了一系列成果。作者在本文中,借鉴其纹理分析的相关方法原理,研究了三维纹理体的提取算法,获得了纹理能量、熵、对比度,以及相关性等纹理属性体,讨论了纹理基元大小选择,灰度级确定,RGB数据融合等应用要素,并在JJD实际工区中取得了较好的应用效果。

1 基于灰度共生矩阵的纹理分析方法

灰度共生矩阵是一种用来分析图像纹理特征的重要方法,它最早由Haralick于1973提出。通过计算图像中一定距离和一定方向的二个像素之间的灰度相关性,可对图像的所有像素进行统计,从而反映出图像在方向、相邻间隔、变化幅度及快慢上的综合信息[14、15]。对于一个已经用灰度来描述的图像G来说,沿着某一方向统计其距离为δ的任意二个像素点,满足一定条件出现的概率p(i,j):

式中 i、j=0、1、2、…、L-1、L为图像的灰度级数;x、y是图像中的像素坐标;g(x,y)是(x,y)处的灰度值;图像的行列数。

在p值经归一化处理后,可写成灰度共生矩阵,形式见式(2)。

容易推知,R是一对称阵,位置偏移δ由x方向和y方向的二个量组成。一般来说,δ较小则反应图像的整体纹理分布,而较大的δ则反应小区域的细微变化。

用灰度共生矩阵可提取多种特征值,最常用的是以下四个特征:

(1)角二阶矩或能量。它是纹理灰度变化均一的度量,反映了灰度分布均匀程度和纹理粗细度。

(2)熵。它可以度量纹理的随机性。当共生矩阵中所有值均相等时,它取得最大值;相反,如果共生矩阵中的值非常不均匀时,其值较小。

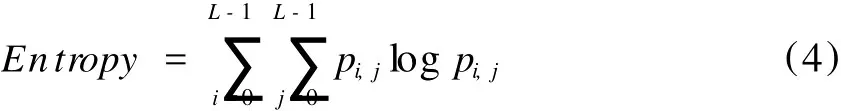
(3)对比度。它是灰度共生矩阵主对角线附近的惯性矩,它度量矩阵值的分布和局部变化,可反映清晰度和纹理的沟纹深浅。

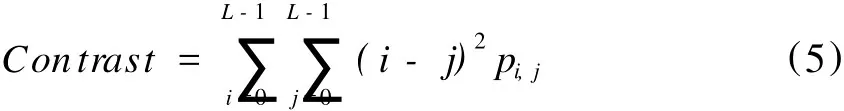
(4)相关性。它度量空间灰度共生矩阵元素在行或列方向上的相似程度。因此,相关值大小反映了局部灰度相关性。

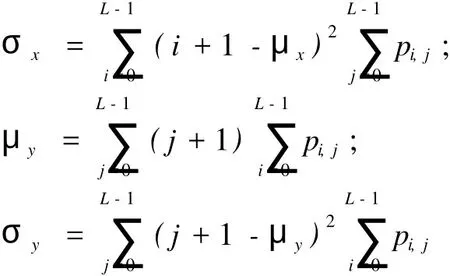
2 三维地震纹理体的提取原理

2.1 纹理基元的引入

地震数据体的振幅用灰度来表示,并按一定的窗去截取数据,可构建地震纹理基元(Texture element)[8]。图1分别展示了以体、剖面和道表示的纹理基元(纹理元)。

图1 地震纹理元示意图Fig.1 The sketch diagram of seismic texture element

2.2 地震资料灰度共生矩阵的构建

地震资料灰度共生矩阵可在地震纹理元基础上构建,它反映了地震纹理体在方向、间隔、变化幅度方面的综合信息。对于图1所示的纹理基元体,其灰度共生矩阵的矩阵元素值可通过下式来计算,即:

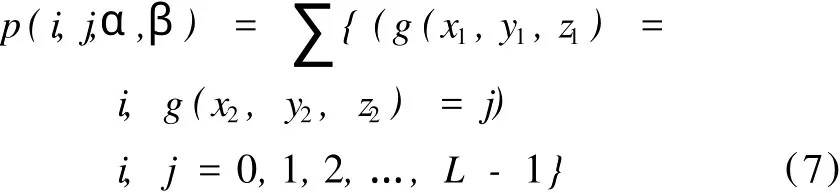
式中 g(x,y,z)为纹理基元体中(x,y,z)点的灰度值;(x1,y1,z1)和(x2,y2,z2)表示距离为δ的二个像素点;∑表示纹理体中沿着某一方向距离为δ的任意二个像素点满足以上条件的概率统计;α、β表示方向(见图2)。特殊地,α=90°,β=0°对应X轴方向;α=0°,β=0°对应Y轴方向;β=90°对应Z轴方向;L表示灰度级数。

图2 纹理基元体的不同方向Fig.2 The different directions of seismic texture element volume

3 实际资料应用及分析

选取胜利油田JJD工区作为应用实例,该区域断裂比较发育,断层和裂缝对油气储集和疏导起主要的作用,因此有效地识别断层和裂缝具有重要的研究价值。在计算时,采用滑动纹理窗,提取的属性包括纹理能量、对比、熵和纹理相关性等四种属性。此外,还讨论了不同的计算方向,时窗大小和灰度级别等应用要素问题。

3.1 不同纹理属性的对比分析

图3(a)为某工区一沿层振幅切片,为了检测断层,用纹理属性来进行分析。通过试验,采用16级灰度级别和9×9×9的三维滑动窗提取纹理体属性,然后抽取沿层切片进行对比分析。这里提取了纹理能量属性(见图3(b)),纹理对比度属性(见图3(c)),纹理熵属性(见图3(d))和纹理相关性属性(见图3(e))。对比图3中四种纹理属性我们发现,以上四种属性基本上都能较好地识别南部大的断层,中部多条断层层次感也比原始切片要好,纹理对比度和相关属性还较好地指示了北部的向斜构造。

3.2 计算方向对属性结果的影响

下面我们讨论纹理的方向性。图4(见下页)给出了在三个不同方向上提取的纹理对比度属性,最后用RGB融合技术对三个方向属性进行融合。从图4中可以发现,不同方向的属性反应的断层是不一样的,其中x方向(横测线方向)较好地反映了东西向的断层;在y方向(主测线方向)上,从图4中还很好地展示出一古河道来,这对油气储集的认识有重要意义;在z方向主要反映深度方向信息,较其它二个方向,此方向提取的属性,断层信息相对要清楚一点。我们还可用数据融合RGB技术,综合三个方向的属性,得到富有层次感、清晰的断层信息。

图3 纹理属性及对比Fig.3 Texture attributes and comparison

3.3 窗口大小对属性结果的影响

纹理计算肯定要涉及到窗口问题,这里以纹理相关性z方向属性为例进行说明。对比图5纹理相关性属性,我们可以发现:图5(a)虽然整体信息比较丰富,但背景噪音相当严重,图像模糊;图5(b)相对好一些,但局部噪音也比较严重;而图5(c)最好,背景噪音少,断层清晰。由此可见,窗口大小对纹理属性影响还是很大的,小窗口背景噪音比较严重,大的窗口则图像清晰,当然太大窗,也会带来信息被平滑掉的问题。通过对比,我们认为9×9×9体窗口比较理想。

3.4 灰度级别对属性结果的影响

在纹理属性提取时,除了要注意窗口大小的选择,还要注意灰度级别的选择。图6(见下页)以纹理相关性z方向属性为例,给出了同一窗口大小,不同灰度级别的属性图对比。从图6中可以看出,并不是灰度级别越大越好,用较大的灰度级别,其内部结构的差异性并不能拉大(见图6(d))。此外,灰度级别越大,计算速度会越慢。对于本区数据,取灰度级为16或32,效果较好。

图4 不同方向的纹理属性对比Fig.4 Texture attributes comparison of different directions

图5 窗口大小对纹理属性的影响对比Fig.5 Texture attributes comparison with differentwindows

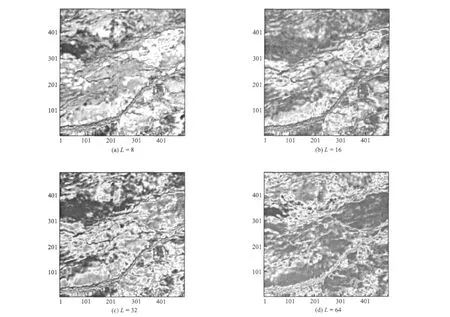
图6 灰度级别对纹理属性的影响对比Fig.6 Texture attributes comparison with different gray levels

4 结论

通过理论分析和实际应用,得到以下认识或结论:

(1)基于灰度共生矩阵提取的纹理属性,是一种很好的凸显断层和裂缝信息的地震属性。

(2)纹理属性提取涉及到方向问题,不同的方向反映的信息不同,可以根据地质需要提取某方向的信息,也可用RGB技术来综合各个方向的信息。

(3)由于纹理属性是体属性提取,与窗口大小有密切关系,要根据不同的情况选取合适的窗,否则容易模糊信息,甚至产生假象。在一般情况下,窗口大小取9×9×9为好。(4)灰度级别对纹理属性结果也有影响,要根据具体情况具体分析,通过试验选择合适的灰度级别。另外,灰度级别还会影响程序的计算速度,灰度级别越大,速度就越慢。综合考虑,对于本工区灰度级别取16或32为好。

[1] 刘晓民.纹理研究及其应用综述[J].测控技术.2008.27(5):4.

[2] 杨淑莹,胡军,曹作良.基于图像纹理分析的目标物体识别方法[J].天津理工学院学报,2001,17(4):31.

[3] 许存禄.图像纹理分析的新方法及其应用[M].上海:复旦大学,2005.

[4] 宋端智,柴振友,张爱敏.用虚拟现实建模语言实现地震层位三维可视化[J].物探化探计算技术,2000,22(3):299.

[5] 郭科,胥泽银,倪根生.用主曲率法研究裂缝性油气藏[J].物探化探计算技术,1998,20(4):335.

[6] DENGL IANG GAO.Volume texture extraction for 3D seismic visualization and interpretation[J].Geophysics.2003,68(4):1294.

[7] DENGLIANG GAO.Texture model regression for effective feature discrimination:Application to seismic facies visualization and interpretation[J].Geophysics,2004,69(4):958.

[8] BAHOR I CH M,FARMER S.3-D Seismic coherency for faults and stratigraphic features[J].The Leading Edge,1995,14(10):1053.

[9] MARFURT K J,KIRL IN R L,STEVEN S L.3-D seismic attributes using a semblance-based coherency algorithm[J].Geophysics,1998,63(4):1150.

[10]GERSZTENKOMn A,MARFURT K J.Eigenstructure based coherence computations as an aid to 3D structural and stratigraphic mapping[J].Geophysics,1999,64(5):1468.

[11]DENGLIANG GAO.Structure-oriented texture model regression:Application to seismic structure visualization and interpretation[J].SEG Expanded Abstracts,2006,25:1083.

[12]DENGL IANG GAO.Application of seismic texturemodel regression to seismic facies characterization and interpretation[J].The Leading Edge,2008,27:394.

[13]DENGLIANG GAO.3D seismic volume visualization and interpretation:An integrated workflow with case studies[J].Geophysics,2009,74(1):W1.

[14]白雪冰,王克奇,王辉.基于灰度共生矩阵的木材纹理分类方法的研究[J].哈尔滨工业大学学报,2005,37(12):1667.

[15]汪黎明,陈健敏,王锐,等.织物褶皱纹理灰度共生矩阵分析[J].青岛大学学报,2003,18(4):5.