基于自回归滑动平均模型的玛纳斯河洪水预报
马金凤,杨 广
(1石河子大学师范学院数学系,石河子,832000;2现代节水灌溉兵团重点实验室/石河子大学水利建筑工程学院,石河子,832000)
水资源是支撑经济增长与可持续发展的最基本的要素之一,而其中径流要素的变化主导着整个系统的变化。由于受气候、社会发展以及人类活动的综合影响,径流变化错综复杂,表现出多时间尺度性、随机性、突变性等特点。因此,径流预测至今仍是国内外研究的热点和难点[1]。20世纪50年代,美国首先建立了世界上最早的水文模型—斯坦福水文模型[2~4],随后水文模型发展迅速,相继有包顿模型(澳大利亚)、萨克拉门托模型(美国天气局水文办公室)、水箱(Tank)模型、BUCKET 模型[5,6]、HBV 模型[7]、SHE模型[8]、SSARR模型[9]等。20世纪70年代初,河海大学建立了新安江模型,在湿润、半湿润地区得到了广泛应用;同期辽宁省水文总站提出了比较完善的超渗产流模型,并在辽河流域首先应用;大伙房水库管理局提出了把蓄满产流和超渗产流概念融为一体的大伙房流域模型,并在东北地区得到了应用。
随着地理信息系统(GIS)以及卫星遥感技术(RS)在水文上的应用,从20世纪90年代初期开始至今,分布式水文模型成为世界上水文领域研究的热点[10~13]。我国虽然在流域模型研究方面引进了一些国外水文预报模型,但是受流域自然地理、水文、气象和人类活动等方面因素的影响,洪水过程预报一直是水文预报中的难点问题[14~16]。
自回归滑动平均模型(ARMA)是一种洪水中长期预报中广泛应用的随机模型,它在计算时不需要其它参证站资料,与一般采用参证站进行延长相比具有一定的优势,同时也为短系列资料延长提供了一种可比的方法。吴玲莉[17]应用门限自回归模型建立了同时受潮汐和径流双重影响的长江下游感潮河段高桥水文站月水位预测模型,结果表明该模型在感潮河段水文要素的非线性时序预测中也具有广泛的实用价值;任政等[18]采用滑动窗口二次自回归模型进行径流中长期预报,结果表明滑动窗口二次自回归模型具有很高的精度,可用于中长期径流预报。
本文基于玛纳斯河肯斯瓦特水文站的径流资料,充分考虑影响洪水的时间和空间信息,建立玛纳斯河洪水预报的自回归滑动平均模型,并检验其适用性和合理性。研究成果可以为下游水库优化调度和合理使用提供可靠的水文信息,提高其经济效益和社会效益,而且还可以广泛应用到其它流域径流预测及其它领域预测中去,为其提供理论和实践参考依据。
1 自回归滑动平均模型(ARMA)的建立
水文系统是受众多因素影响的复杂系统,影响因素大多具有非确定性的时变特征。因此,水文系统是一个非确定性的动态系统,可用时变参数随机系统模型来描述非确定性动态水文系统[11]。由于所研究流域处于干旱半干旱地区,为高寒山区流域水文气象资料代表性较差,影响径流的水文气象因素较多,要建立较为复杂的、考虑到诸多因素的预报模型,变得非常困难。因此,建立结构简单又能反映流域时变特征的ARMA(p,q)水文预报模型。利用现有的水文和气象资料,通过最小信息准则(AIC),确定模型的最佳阶数,采用实时校正的可变遗忘因子递推最小二乘法,依据历史资料对该模型进行了验证。
构建结构简单便于实际操作的自回归滑动平均模型,即ARMA模型:

式(1)中:ζt为 t日的平均流量预报值,ζt-p为 t日之前第 p天的日平均流量实测值(p=1,2,……,M),M为滑动计算时的步长(d);еt-1为 t日之前1天日平均流量的预报误差;φp为第 p个自回归系数;θ1可视为预报误差修正系数。
气温和降雨是影响冰雪融水或降雨冰雪融水的混合补给型河流径流的主要因素,设置气温及降雨修正函数 T(t),P(t)。因此,非平稳时间序列的预报方程概化为:
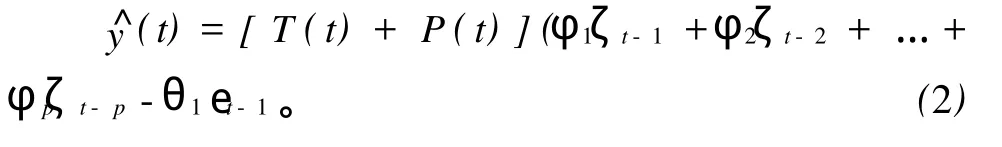
2 ARMA模型的应用及分析
2.1 流域水文、气候概况
玛纳斯河流域位于新疆准噶尔盆地南缘,发源于天山北坡 ,位于 43°20′~45°55′N,85°00′~87°00′E,全长约400km,流域面积5156km2,是准噶尔盆地最长的内陆河。该流域气候属典型的大陆性干旱气候,夏季气温高,降水多;冬季寒冷,降水少,因此玛纳斯河水流量冬季小,夏季大。最小流量2.0m3/s(1964年1月23日),最大流量1095m3/s(1999年8月2日)。山区集水面积5156km2,最大年径流量19.15×108m3(1999年),最小年径流 10.09×108m3(1992年),多年平均流量40.6m3/s。该流域地形呈南高北低走势,河源区的年降水量可达600~700mm,而在山前平原区则降至100~200mm。山区降水成为玛纳斯河的主要径流补给。在12.80×108m3的年总径流量中(肯斯瓦特水文站),冰川融水补给的比重将占34.6%。冰雪融水已成为天山北坡绿洲灌溉的宝贵水源,使玛纳斯河流域成为我国的第四大灌区。因此,选择适当的数学模型,对玛纳斯河的径流做出模拟与预测具有重要的应用价值与指导意义。
该流域水系如图1所示。
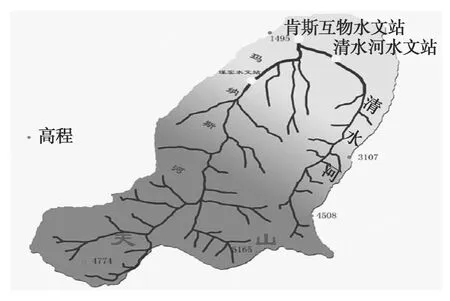
图1 玛纳斯河流域水系Fig.1 Water system of the Manas River Basin
2.2 玛纳斯河径流量年际变化趋势分析
选取序列最长、资料最完整的玛纳斯河肯斯瓦特站径流资料进行分析。通过统计分析得出玛纳斯河径流量历年平均为12.95×108m3,70年代以前年均为12.946×108m3,70年代年均为12.008×108m3,80年代年均为12.28×108m3,90年代以来年均为14.572×108m3,90年代比80年代径流增加了18.7%。
图2是玛纳斯河1954~1999年年平均径流量的变化曲线,从90年代中期开始年径流量增加显著,这与气温在90年代显著升高,降水在90年代显著增加有着重要关系。总之这45年间玛纳斯河径流量变化是比较复杂的,这与径流量变化受多种因素的影响有关。
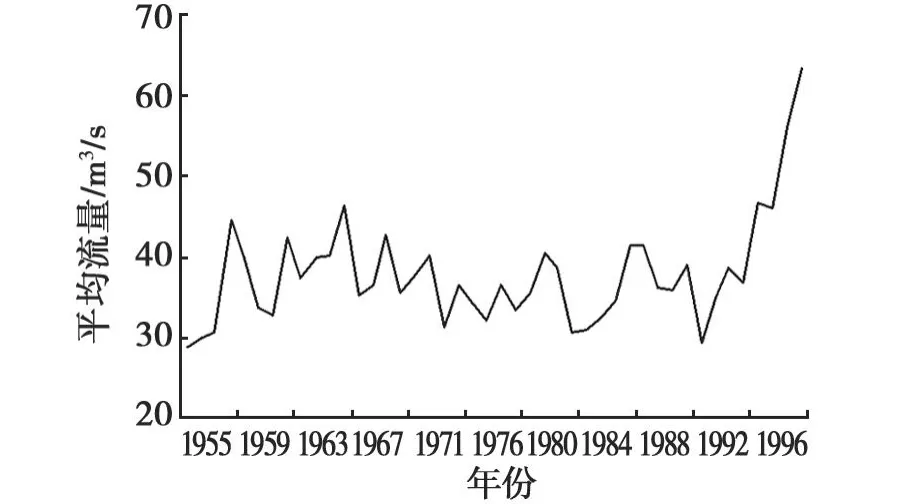
图2 玛纳斯河径流年际变化Fig.2 The runoff change of the Mana s River
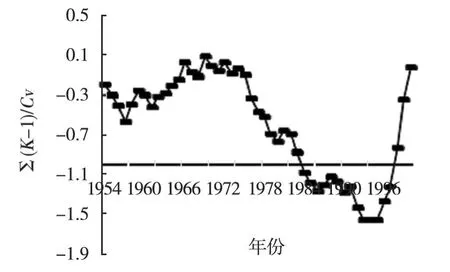
图3 玛纳斯河年径流量模比系数差积曲线 Fig.3 ARMA model forecast result contrastwith the measure date
模比系数差积曲线主要反映径流或降水序列是否经历丰水和枯水过程,累积平均过程线即为序列值是否平稳。差积曲线的上升段反映丰水期,下降段反映枯水期。
从玛纳斯河(肯斯瓦特站)年径流量模比系数差积曲线(图3)可见,玛纳斯河年径流变化过程可分为几个显著阶段,1954~1957年为枯水期,1958~1969年为丰水年段,1970~1975年平水段,1976~1986年是枯水段,1987年以后径流量是增加的,从90年代中期开始年径流量增加显著。
2.3 模型应用
ARMA(p,q)模型的适用性主要取决于模型阶数的选择和参数的率定方法。要建立较为理想的ARMA(p,q)预报模型,仅靠一次猜测就建立某一阶数模型是不行的,而应对不同的 p,q阶数来进行试验,以便选择出最佳的 p,q来建立最终的预报模型。但在实际预报中,残差方差最小的预报模型不一定预报效果最好。因而,选择 p,q阶数标准通常采用最小信息准则(AIC)或动态建模方案。动态建模是逐个地用一系列ARMA(m,m-1)(m=1,2,…)模型来逼近数据,逼近效果将由模型的残差平方和减少的程度来判断。
从表1和表2可以看出:玛纳斯河年径流过程模拟相对误差较小,洪峰流量预报结果合格率较高,对实测资料具有很好的逼近拟合效果,说明自回归滑动平均模型用于径流量预测具有较高的精度,是可行的。

图3 ARMA模型预测结果对比Fig.3 ARMA model forecast result contra stwith the measure date
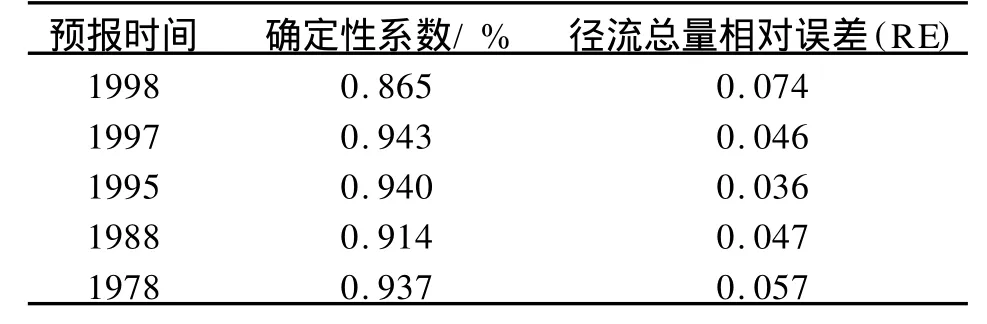
表1 玛纳斯河年径流过程模拟检验成果Tab.1 The check of runoff simulation in the Manas River
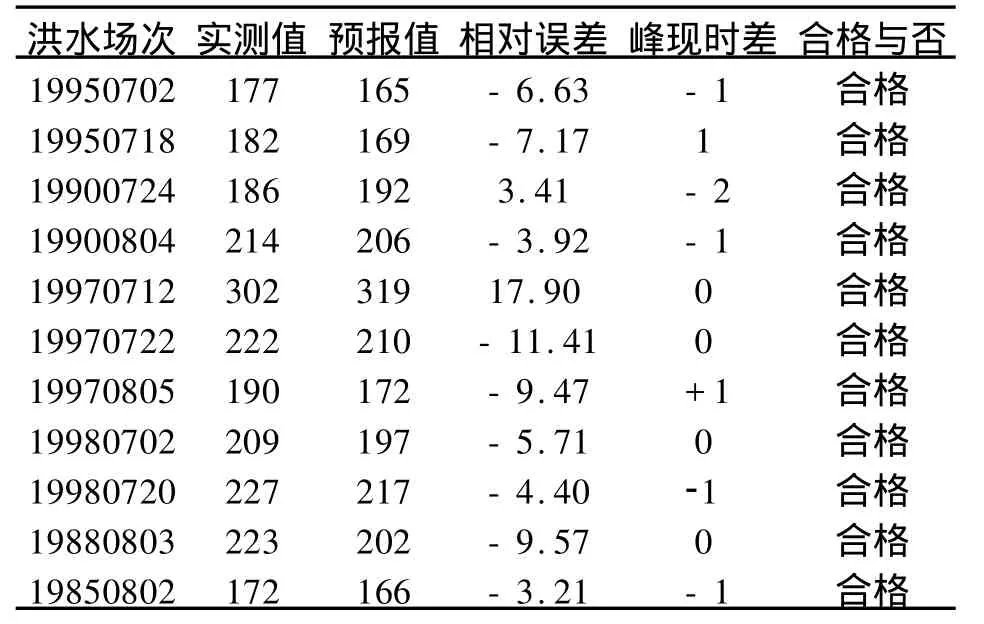
表2 模型的洪峰流量统计结果Tab.2 Flood peak flux statistical result in the model
3 结论
1)近40年来,玛纳斯河径流量的年际变化出现了几个丰枯水期,1987年以后年径流量变化呈现出稳定增加趋势,到90年代中期年径流量增加趋势显著。径流量年内分配极不均匀,集中程度高,而径流的年变差系数CV值小,径流量多年变化比较稳定。
2)从玛纳斯河年径流过程模拟及洪峰流量预测结果来看,ARMA(p,q)模型对玛纳斯河流域径流量预测具有很强的适用性,不需要其它参证站资料,简单方便且预测精度较高,能够满足对玛纳斯河流域洪水预报的要求,具有较好的应用价值。
[1]刘海超,施雅风.中国冰川资源及其分布特征—中国冰川目录编制完成[J].冰川冻土,2002,22(2):106-112.
[2]赵人俊.流域水文模拟[M].北京:水利电力出版社,1984.
[3]刘金清,陆建华.国内外水文模型概论[J].水文,1996,(4):4-8.
[4]E L Peck. Catchment modeling and initial parameter estimation for the national weather service river forcasting system http :/ / www. crh. noaa. gov/crh/ [ J ] . office of hydrology washingt on D. C J une ,1986 :20-24.
[5]Atkinson S E ,R A Woods ,M Sivapalan. Climate andlandscape cont rols on water balance model complexity over changing timescales [J] . Water Resource Res ,2002 ,38 (12) :501-506.
[6]Farmer D M Sivapalan ,C Jothityangkoon. Climate , soil ,and vegetation cont rols upon the variability of water balance in temperate and semiarid landscapes : Downward approach to water balance analysis[J ]. Water Resour Res ,2003 ,39 (2) :1-19.
[7]C Jothityangkoon ,M Sivapalan ,D L Farmer. Processcont rols of water balance variability in a large semi-aridcatchment : downward approach to hydrological model development [ J ] . Journal of Hydrology , 2001 , 25 ( 4) :174-198.
[8]Lindst rom , Goran , Johansson , et al. Development and test of the dismbuted HBV 96 hydrological model [J] .Journal of Hydrology ,1997 ,20 (1) :272-288.
[9]Abbott M B ,Bathurst J C ,Cunge J A ,et al. An int roduction to the European Hydrologic System Hydrologique European , SHE[J ] . Journal of Hydrology,1986 ,87 :45-47.
[10]万洪涛,万 庆,周成虎.流域水文模型研究的进展[J].地球信息科学,2000,(4):46-49.
[11]张 伟.基于人工神经网络的径流预测研究[D].石河子:石河子大学,2008:45-60.
[12]马吉刚,崔远来,沈细中,等.水库来水量预测的进化神经网络法[J].中国农村水利水电,2005,(2):35-37.
[13]许楚杰.预报模型的组合及其在韩江流域洪水预报中的应用[J].水利科技与经济,2009,(7):574-574,577.
[14]张 俊.基于 GIS的汉江流域洪水预报系统设计与实现[J].长江科学院院报,2009,(8):15-19.
[15]赵 琪.神经网络模型在中长期水文预报中的实用性探究[J].新疆水利,2008,(6):20-22.
[16]张建新.基于WebGIS的洪水预报技术概述[J].水文,2008,(5):48-52.
[17]吴玲莉,张 玮.遗传门限自回归模型在感潮河段水位预测中的应用[J].水利水电科技进展,2005,25(5):20-23.
[18]任 政,郝振纯.滑动窗口二次自回归模型在径流预报中的应用[J].河海大学学报(自然科学版),2009,37(3):267-270.

