关于多元微积分基本定理与Stokes公式的注记

罗玉文

(重庆理工大学数学与统计学院, 重庆 400050)

0 引 论

对于一元函数来说,理解了Newton-Leibniz公式,就理解了全部的微积分.因为这个公式包含了微分与积分的全部的内在关系,所以我们称这个公式为微积分基本定理.对于多元函数来说,我们也有微分与积分的概念,那么,什么是多元函数微积分的基本定理呢?也就是说,什么是体现多元函数微分与积分的内在联系的公式呢?

通过对Newton-Leibniz公式的分析,我们就会发现,Newton-Leibniz公式说明的是：函数在区间边界是的值,等于函数的微分在区间内部的积分.如果依此分析,那么不难感觉到,在平面上,微积分的基本定理就应该是Green公式[1],在空间的情形,应该就是Gauss公式,而在曲面上,微积分基本定理就应该是Stokes公式.而事实确实如此,但是要说明这一事实,不是一件容易的事,这里要用到外微分的概念.更进一步,这三个公式与Newton-Leibniz公式一起,在外微分的柜架下,可以用一个公式统一来表示,这就是广义的Stokes公式.现在我们来叙述这一事实.

1 外微分

首先,我们定义外微分算子 d为满足如下条件的微分算子[2-3]：

1.d2x= d(dx);

2.dxdy=-dydx;

3.如果f为一普通函数,则 df为f的全微分.

我们再定义外微分形式如下[4]：

1.函数为零次外微分式;

2.一次外微分式为形如fidxi的线性组合,其中 fi为一函数;

3.二次外微分式为形如fijdxidxj的线性组合,其中fij为一函数;

4.三次外微分式为形如fijkdxidxjdxk的线性组合,其中 fijk为一函数.

例如,f(x)dx为一次外微分式,Pdx+Qdy也是一次外微分式,Pdxdy+Qdydz是二次外微分式,Rdxdydz为三次外微分式.

再如,由外微分算子的定义,我们有

Pdxdy=-Pdydx,

而

上式中用到了 d2x=d2y=0,dxdx=0以及 dxdy=-dydx.

2 广义Stokes公式

为了本文的需要,我们将广义Stokes公式叙述成我们所要的形式

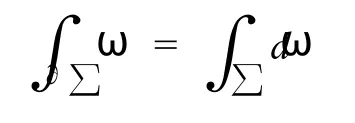
这里积分的重数与区域的维数一致.

这个公式的证明需要用到较多的流形的知识,我们略过,有兴趣的读者,可以参考本文所附文献.

现在我们来说明,Green公式,Gauss公式和通常的Stokes公式,就是多元函数微积分的基本定理,而且都可以用广义Stokes公式来表示.

首先,我们设

ω= P(x,y)dx+Q(x,y)dy

由第二节的计算,我们得到

代入广义Stokes公式,我们就得到了Green公式[1].

再设

ω= P(x,y,z)dxdy+Q(x,y,z)dydz+R(x,y,z)dzdx

我们得到

再次代入广义Stokes公式,我们就得到了Gauss公式[1].

最后,我们设

ω=Pdx+Qdy+Rdz

其中 P,Q,R为x,y,z的三元函数,类似于上述计算,我们得到

由广义的Stokes公式,我们就得到了通常的Stokes公式[1].

同样的道理,Newton-Leibniz公式也可以由广义Stokes公式来表示.事实上,广义Stokes公式不止在三维以下的空间成立,在更一般维数的空间上都是成立的.在一维、二维、三维欧氏空间及曲面上,它的特殊形式就是Newton-Leibniz公式、Green公式、Gauss公式及Stokes公式.这个公式说明了外微分式在边界上和积分与其外微分在区域内部的积分之间的联系,它表达了微分与积分之间的内在联系,所以它是所有维数下的微积分的基本定理,是微积分理论的顶峰与终点,是所有微积分理论的全部核心与关键.理解了这个公式,也就理解了全部的微积分.

[1]陈传璋,等.数学分析 (下)[M].上海：上海科学技术出版社,1988：334-335.

[2]陈省身,陈维桓.微分几何讲义 (第二版)[M].北京：北京大学出版社,2001：74-78.

[4]Steven H.Weintraub,Dierential forms,A complement to vector calculus[M].Acdemic Press,Inc.,San Diego,1997：1-34.

[5]Spivak.Calculus on manifolds[M].W.A.Benjamin,Inc.,New York,1965：109-137.