整流滤波电压算法探讨

麻幼学

（肇庆学院 电子信息与机电工程学院,广东 肇庆 526061）

有人在进行近似计算时,将整流滤波电路的输出电压波形以锯齿波表示.采用这种计算方法,锯齿波违反了电路元件特性的约束(VCR)和拓扑约束(由KCL和KVL体现),还违背了基本物理定律,而且所得结论并不能覆盖RLC的全部变化范围.另外,作为教学基础的教材,其一切论断和方法都应成为遵守基本定律的典范,而不是违背基本定律的向导,因此,这种近似计算方法值得商榷.本文中,笔者以文献［1］510－512为例进行讨论,指出其错误所在,并给出正确的近似分析计算方法.

1 整流滤波输出直流电压计算方法存在的问题

文献［1］510的单相桥式整流电容滤波电路如图1所示.其认为可将电容滤波的电压波形（如图2实线所示）近似为锯齿波,如图3所示.图中T为电网电压的周期.设整流电路内阻较小而RLC较大,电容每次充电均可达到电源电压u2的峰值(即UOmax＝U2),然后按RLC放电的起始斜率直线下降,经RLC交于横轴,且在T/2处的数值为最小值UOmin,则输出电压的平均值为

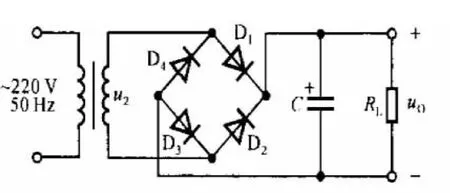
图1 单相桥式整流电容滤波电路

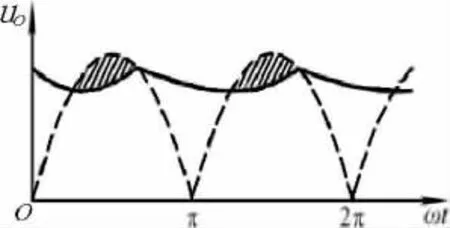
图2 电容滤波的电压波形

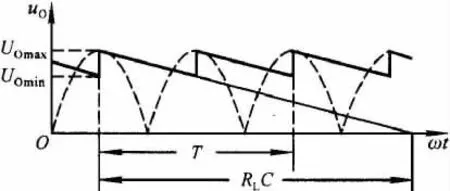
图3 锯齿波电压波形

同时,按相似三角形的关系可得

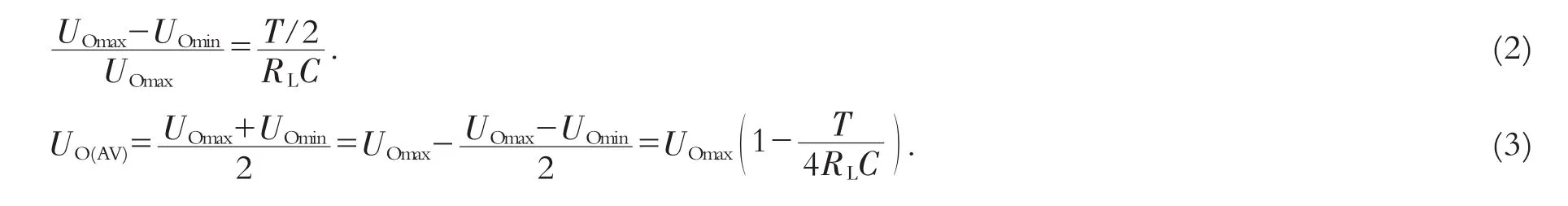
因而

仔细研究上述内容,可发现如下2个问题：

1)电压“按RLC放电的起始斜率直线下降”及“电容滤波的电压波形近似为锯齿波”,违反电路基本定理和能量守恒定律.

2)输出电压平均值的计算公式(4)不能覆盖RLC的全部变化范围.比如：当RLC≤T/4时,式(4)的计算结果竟然为小于零的负数.

2 问题分析

首先,根据图1电路的拓扑结构,电容放电电压不会“按RLC放电的起始斜率直线下降”.因为当二极管截止、电容放电时,电容上的电压也是电阻RL上的电压.若按直线规律下降,则电容放电电流的大小不变,但是流过电阻RL上的电流却像电压一样“直线下降”,这种现象违反了克希霍夫电流定律(KCL).其次,输出电压uO的波形不会形成锯齿波,因为违反电路中二极管的伏安特性.电路中的二极管已被文献［1］510设定为与图2波形相吻合的伏安特性——二极管正偏电压小于零时截止,等于零时导通且导通电阻为零（伏安特性一旦确定就不可随意改变.因为电路只受拓扑约束(由KCL和KVL体现)及元件特性约束(VCR),任何一种约束的改变,等同于电路被改变）.这样的伏安特性是不可能产生图3所示的锯齿波电压的.实际上不存在实现锯齿波的二极管,因为与实现锯齿波相匹配的二极管的伏安特性必须如图4所示.当正偏电压uD从零开始增大直至uON的过程中,电流iD为零（如图4与横轴重合的线段①所示）.当uD＝uON时,二极管导通.此后正偏电压uD从uON开始减小直至为零的过程中,任何电压所对应的导通电流iD均保持无穷大（对应的伏安特性曲线在坐标平面上是连续分布的,图4②组线段所示意的只是无限曲线中的几条而已）,这样才能符合锯齿波电压的垂直上升部分对二极管电流与电压变化的要求.如此伏安特性的二极管是根本不存在的.第三,与图3所示锯齿波电压对应的电容C的电流波形,只能是电容C放电时电流不变,而充电时电流无穷大,这是严重违反能量守恒定律的.因为交流电源不可能为电容C提供无穷大的充电能量.在电容放电期间,锯齿波电压同样违反能量守恒定律.因为电容C的放电电流与流过电阻RL上的电流不相等,因此电荷守恒定律被破坏,所以能量守恒定律也遭到破坏.第四,由公式(4)即可发现:当RLC≤T/4时,输出电压的平均值UO(AV)≤0,这是与电路实际输出电压平均值不符且无法解释的数值.由此进一步证明了锯齿波根本不是电容滤波电路正确的近似波形.

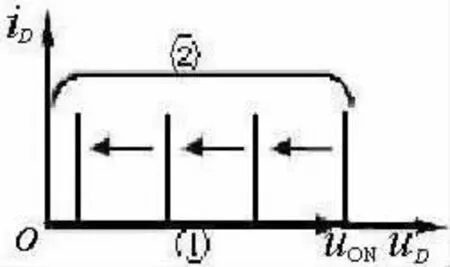
图4 产生锯齿波电压的二极管伏安特性

3 输出电压平均值计算

图2实线所示的电压波形难以用解析式来描述,分析计算也难以实现；但是,借助图5所示的输出电压波形对其进行分析计算,不仅可以有理有据地显示教学内容,而且其结论对工程设计也具有指导意义.

由图5可知t2之前为电容C充电的过程,二极管导通电流iD为

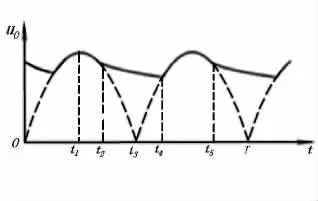
图5 电容滤波的电压波形

式中：

分别为电阻RL和电容C上的电流.到t2时刻二极管截止,此时iD＝0,即

由此可得

即

由图5的波形可知,t4时刻有如下表达式：

式（11）也可改写为如下形式：

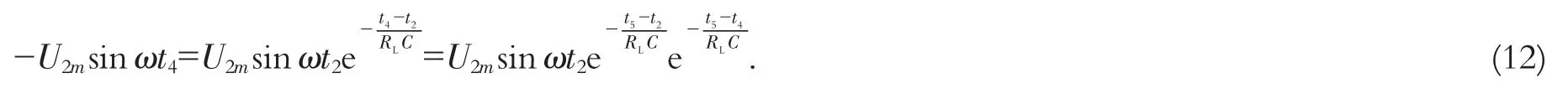
通常为了取得更好的滤波效果,RLC选取得比较大,常取RLC≥(3～5)T/2,使得电容C的放电时间远大于其充电时间.(t5－t4)≪T/2,则(t5－t4)/RLC≈0,即(t4－t2)≈(t5－t2).故上式可近似为

求得

式中,t5是图5所示波形中电容C再次放电的时刻.由波形可知

代入式(14),即得

由图5所示波形可写出输出电压uO的函数表达式为

将输出电压uO按傅里叶级数展开得

直流分量

因为

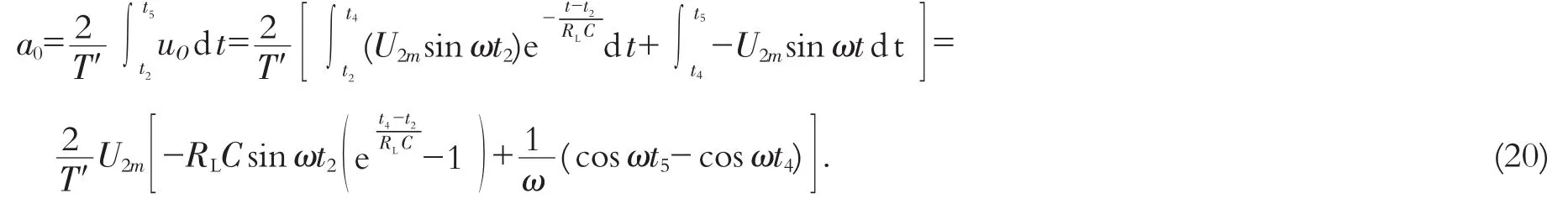
式中

为输出电压uO的变化周期.综合(19)～(21)且考虑到ωT＝2π,经整理后可得输出电压uO的直流分量

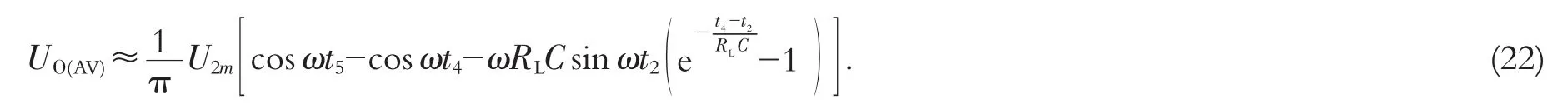
如果取RLC等于5倍的T/2,则由式(10)得

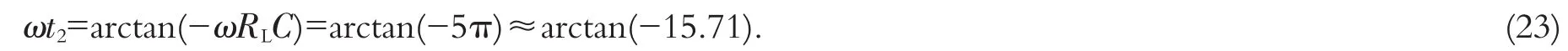
查数表[2]324可得

由式(16)和(24)得到

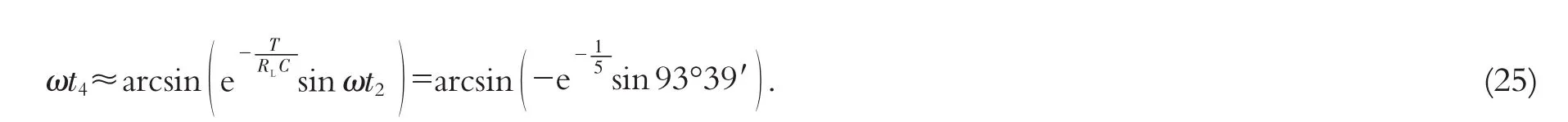
由数表[2]318查得＝0.8187.代入式(25)并由数表[2]321查得

将(15),(24),(26)代入(22),即得

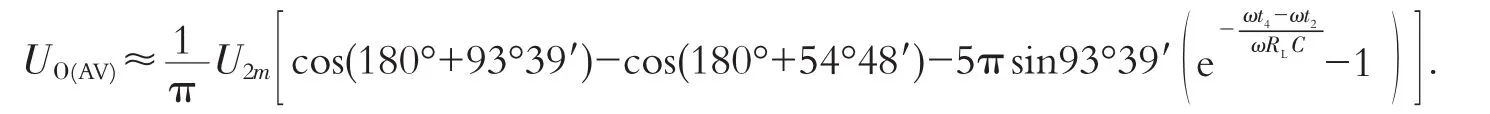
经查表[2]318－329并整理后得

该结果与经典的实验曲线[3]数据一致.

当RLC→0时,由式（10）和（16）知,ωt2→π,ωt4→π,ωt5→2π.通过式（22）算得输出直流电压为

由公式(8)可知RL≠0；否则,有限的电容放电电流不能满足无限大的电阻电流,此式不成立.这样,电容放电开始于ωt2→π,结束于ωt4→π,为同一时刻.由图5的波形知电容放电的持续时间为零,电压也为零.该现象意味着电容充、放电活动已经停止,滤波作用已经消失,输出电压波形与整流输出波形相同,输出直流电压与整流输出直流电压相同.

当RLC→∞时,由式（10）和（16）知,ωt2→π/2,ωt4→3π/2,ωt5→3π/2,说明此时电容充电后已无放电路径,输出电压uO始终维持在最大值.根据洛比达法则[4],由式（22）算得输出直流电压为

由此证明电路输出电压稳定在电源电压u2的峰值.

计算数据证明,公式(22)能够很好地吻合整流滤波电路的实际情况,可以覆盖RLC从0到∞的全部变化范围.说明该近似分析计算方法不仅遵守基本定律,而且数据精确、易于计算.

[1] 童诗白,华成英.模拟电子技术基础[M].北京:高等教育出版社,2001.

[2] 中国矿业学院数学教研室.数学手册[M].北京:科学出版社,1980.

[3] 南京工学院无线电工程系《电子线路》编写组.电子线路:第5册[M].北京:高等教育出版社,1979:19.

[4] 宋开泰,黄象鼎.高等数学教程:上册［M].武汉:武汉大学出版社,1998:365-372.