基于分层Boussinesq类模型的深水波数值模拟
余向军,张永刚
(海军大连舰艇学院 科研部,辽宁 大连 116018)
基于分层Boussinesq类模型的深水波数值模拟
余向军,张永刚
(海军大连舰艇学院 科研部,辽宁 大连 116018)
波群演化有非常特殊的物理现象。模拟这一过程要求模型具有较好的色散性性能同时具有良好的波幅离散性能、非线性性能。采用分层Boussinesq类方程对深水波群得到非线性演化开展数值模拟研究。利用Stansberg(1993)的物理实验验证了分层Boussinesq方程波浪模型在该研究中具有很好的适用性和较高的精度。模型较好地预报了组成波的倍频、和频及差频波浪。越接近造波板,结果吻合的越好。随着长时间的演化,主频部分的组成波的波高数值结果要大于实测结果,高频部分的组成波出现明显差异。
分层Boussinesq类模型;深水波;数值模拟
引言
经典的Boussinesq方程仅适用于浅水,但自Boussinesq推导出Boussinesq方程以来,Boussinesq方程已经有了很大的发展,Boussinesq方程的一个重要发展趋势是将该方程的适用水深由浅水向深水扩展。
Peregrine首先把它推广到可应用在二维变水深的情况下[1]。Madsen等提出了改进色散性的新型Boussinesq方程[2]。模型在线性上精确到μ=3,尽管非线性在μ>1时存在很大错误。随后Madsen等人又将他们的方程推广到适用于缓变地形较为一般的地形。Nwogu提出了以任意水深处速度表示的Boussinesq方程[3],它和Madsen提出的方程是目前弱非线性Boussinesq类方程的代表性方程,并被一些学者(如Beji和Battjies;Wei和 Kirby;Kaihatu 和 Kirby等)用来研究比较复杂地形上的波浪变形问题。自 Madsen和 Sorensen(1992)、Nwogu(1993)的工作以来,Boussinesq模型在把深度积分方程应用于深水中取得了巨大进展。Liu(1994)和Wei等(1995)扩展Nwogu方法于完全非线性波,这导致模型不仅可应用于中等水深,也适用于模拟强非线性相互作用。然而,这些方程的非线性准确性仍低于色散性的准确性。为了进一步应用于深水,需采用高阶Boussinesq类方程。前面叙述的模型均应用二次多项式描述垂直流场分布,高阶模型应用四阶甚至更高阶的多项式。Gobbi(2000)[4]使用四阶多项式推导的模型,线性色散性精确到μ≈6,色散性精确到μ≈3。Madsen等(2002)基于 Agnon(1999)的方法提出了一个 Boussinesq类模型,准确性达到极其深水(μ≈40)。这一方法不同于本文前面所述模型的方法,采用Laplace方程的最优展开,适用于深水。通过使用水柱不同层的多级展开,只需要五阶空间导数就可以达到深水的准确性。然而,Madsen模型相对于高阶模型,比如Gobbi的模型,需要更多的方程和未知量。
Lynett和Philip Liu提出了基于Boussinesq方程的波浪分层数学模型[5],在传统的Boussinesq方程基础上再一次对垂直方向进行分层。同时假定在每一层中的垂向流速按线性分布,分别在各层对垂向流速进行垂向积分,求其平均流速,用这一平均流速来代替每一层的垂向流速。这样处理不仅在精度上比以前的Boussinesq方程模型有所提高,而且更为重要的是提高了模型的色散性,使模型方程能应用于更大的水深。
1 物理模型
Lynett和Philip Liu提出的分层模型如图1所示[6]。在垂直方向上将水柱分解成多层(N层),采用一种深度积分模型来代替对垂直流场的高阶多项式近似,利用多重二次多项式,并匹配各层之间的交界面。由于没有高阶的空间求导和高阶的多项式近似,这种方法能产生出一种精确的模型。利用任意N层,通过对原始运动方程进行分段积分,可以获得一系列的模型方程。这样,将整个水柱流速断面分解成N个层,每一层中都独立地确定一个流速断面,再加上层与层之间的交界面,于是方程的一系列解由 (2N-1)个自由参数组成,这样可以对水波的已知的解析解进行优化。通过对原始运动方程进行积分,形成一系列的方程式,积分将分段进行。
如图 1 所示,ζ'(x',y',t')表示在水深 h'(x',y',t')处传播的波列的自由表面位移。层与层之间的边界定义为η'n(x',y',t')。 水柱面被分成 N 层,上边界为 η'0=ζ',下边界为 η'N=-h'。所有其他边界设定为η'n=βnh',其中βn是任意的。由于h'是时间t'的函数,η'n也是。每一层均有一个特定厚度dn。将层厚度dn作为相应层的垂直尺度,h0为特征水深,特征波长l0=l/k作为水平长度尺度,作为时间尺度,k为波数,a0作为波浪运动的幅度,定义如下无量纲:
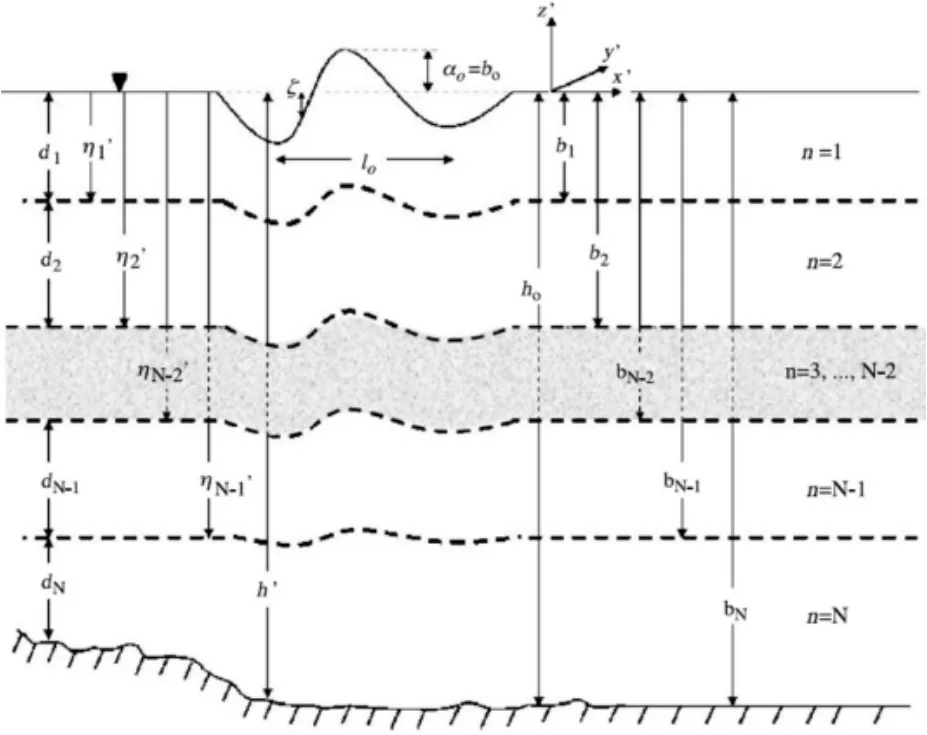
图1 分层Boussinesq方程N层模型示意图
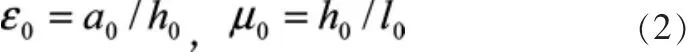
假设粘性影响是可以忽略的,波浪运动可以用连续方程和欧拉方程描述为:
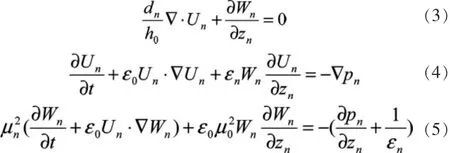
对方程进行小参数展开,无量纲物理量可展开为:

通过推导,得到三个控制方程。
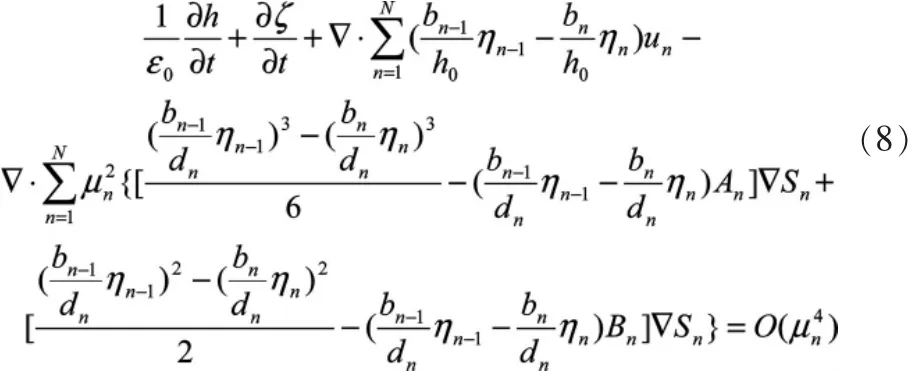
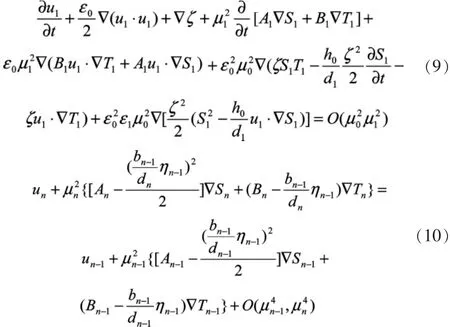
低层速度可以通过上层速度直接计算。方程 (8),(9),(10)是一组以un和ζ形式给出的强非线性频散波的控制方程。
2 数值模拟与验证
波群演化是非常特殊的物理过程。非线性使具有不同波幅的波浪传播速度各异,即波幅离散。对于波群,其中具有较大波幅的组成波的传播速度大于具有小波幅组成波的传播速度,这将导致波群前部的波压缩而波群尾部的波拉伸,最终形成波群形状的不对称。除波群形状产生不对称外,波群在沿水槽演化过程中将产生具有新频率的波浪成分,这是由于四波共振解谐产生的[7]。模拟这一过程要求模型具有较好的色散性性能同时具有良好的波幅离散性能、非线性性能。本文采用分层Boussniesq类模型对于深水波群非线性演化进行数值模拟。
这里针对Stansberg做的深水波实验进行模拟[8]。Stansberg在挪威MARINTEK大水槽进行实验,实验水槽长270 m,前80 m水深10 m,其他区域水深5 m。入射波为双色波群,波周期分别为1.9 s和2.1 s。每个组成波波高为0.16 m。传感器分别放置在距离造波机 9.3 m,40 m,80 m,120 m,160 m和200 m处。图2,图3,图4分别为9.3 m,80 m,120 m处实测值与模拟值的比较分析。从图中可以看出,越接近造波板,模拟结果与实测结果吻合的越好。图2可以看出,数值模拟的波浪在沿水槽传播过程中基本保持同造波板附近波浪信号相似的形态,波群依然左右对称,模拟结果与实测结果吻合较好。进一步分析其频谱组成,对于实测值,造波板附近的频谱谱峰值和理论值一致,说明模拟效果良好。在图3中可以明显地看到波群的频谱组成发生了变化,即频谱峰值不再对称,同时有了新频率组成波的产生,对于实测值,造波板附近的频谱谱峰值和理论值并不完全一致,数值模拟的主频要小于实测结果,高频部分吻合较好。在图4中可以明显地看到波群的频谱组成进一步变化,次频增多,高频部分实测结果与模拟结果不完全一致。
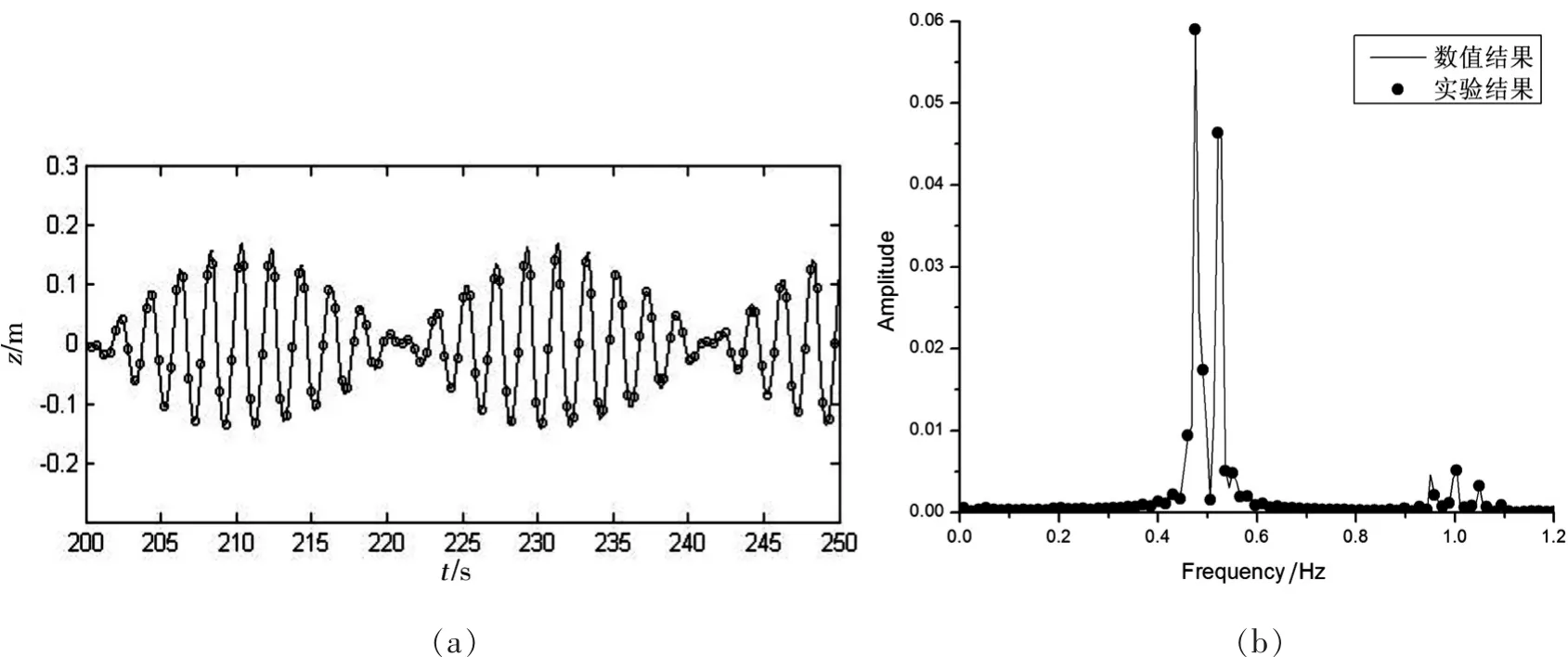
图2 9.3 m处的模拟结果与实验结果比较分析图
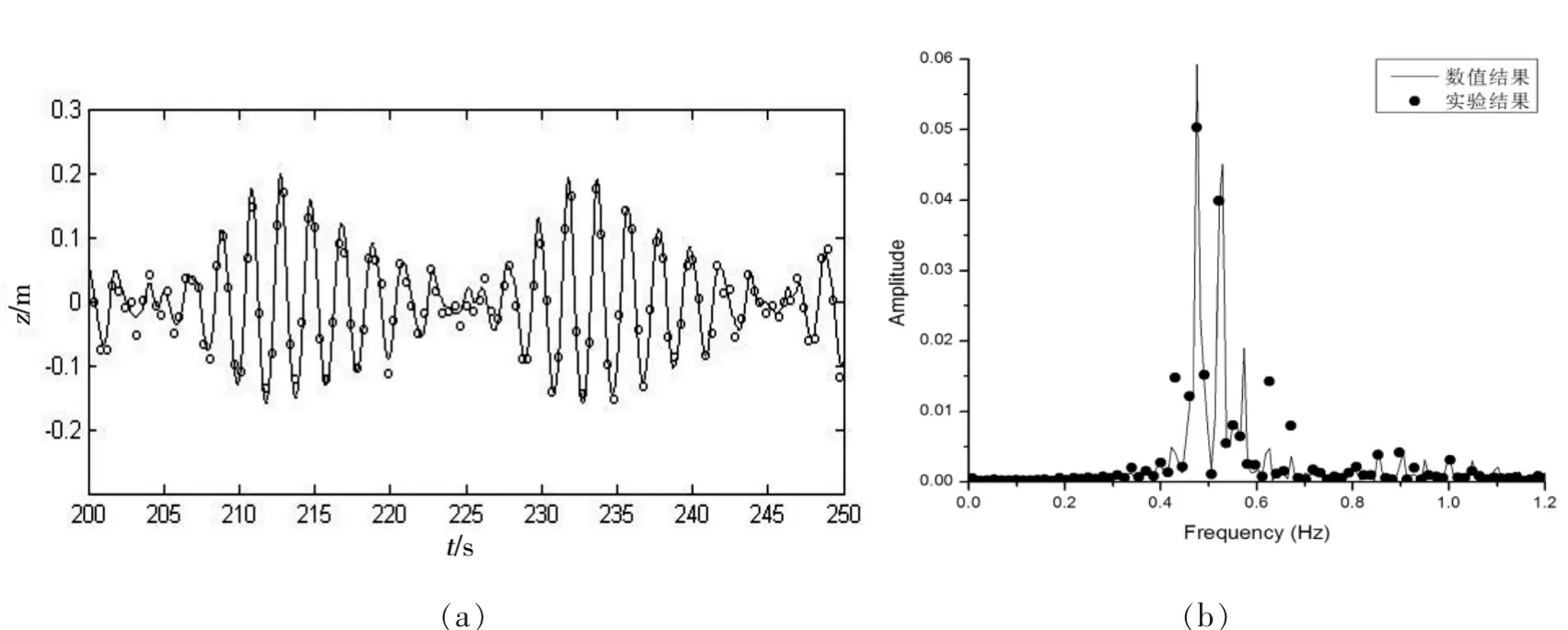
图3 80 m处的模拟结果与实验结果比较分析图

图4 120 m处的模拟结果与实验结果比较分析图
3 结论
本文在总结前人研究工作的基础上,运用分层Boussinesq方程对深水波群进行数值模拟。利用试验数据验证了分层Boussinesq方程波浪模型在该研究中具有很好的适用性和较高的精度。在造波板附近,三组时间序列给出的谱形与实测结果基本一致,都比较好地预报出了组成波的倍频、和频及差频波浪。但波群经过长时间演化后,在x=80 m,120 m处给出的结果存在明显差异。主频部分的组成波的波高数值结果要大于实测结果,分析原因是由于实验误差造成的;随着波浪非线性演化,高频部分组成波变得不一致,这主要是因为数值模型采用二层模型,μ值超出范围。比如频率在1 Hz的组成波,μ=10,超出精度范围,因此计算结果出现较大误差,采用三层模型能提高高频部分精度。
[1]Peregrine D H.Long waves on a beach[J].Fluid Mech,1967,27:815-827.
[2]Madsen P A,Sorensen O R.A new form of the Boussinesq equations with improved linear dispersion characteristics:Part II.A slowly varying bathymetry[J].Coast Eng, 1992,18:183–204.
[3]Nwogu O.Alternative form of Boussinesq equations for nearshore wave propagation[J].Waterw Port Coast Ocean Eng, 1993,119(6):618-638.
[4]Gobbi M F,Kirby J T.Wave evolution over submerged sills:tests of a high-order Boussinesq model[J].Coast Eng,1999,37:57-96.
[5]Lynett P,Liu P L-F.A two-dimensional,depth-integrated model for internal wave propagation[J].Wave Motion in press.2002,36:221-240.
[6]Patrick Lynett.A multi-layer approach to modeling generation propagation and interaction of water waves[D].USA:CornellUniversity,2002.
[7]邹志利.水波理论极其应用[M].北京:科学出版社,2005.
[8]Patrick Lynett.A multi-layer app roach to modeling generation p ropagation and interaction of water waves[D].USA:CornellUniversity,2002.
Numerical Simulation of Deep Water Wave Group Using a Layered Boussinesq-type Equation
YU Xiang-jun,ZHANG Yong-gang
(Dept.of Scientific Research,Dalian Naval Academy,Dalian Liaoning 116018,China)
Deep wave evolvement is a very different phenomenon in the nature.Thus,simulating the phenomenon needs the model to have high dispersion and high nonlinear accuracy.Deep wave evolvement is simulated by two-layer,depth-integrated Boussinesq model.The proposed numerical model is examined by comparison with the experimental results which come from Stansberg’s experiment(1993).The numerical result shows that the layer,depth-integrated Boussinesq model have good applicability and precision in the simulation of deep wave evolvement.The proposed numerical model predicts well diploid-frequency components,sumfrequency components and difference-frequency components.When it is closer to the wavemaker,the experimental-numerical comparisons become more consistent.With the time developing,wave amplitude in the main frequency is less than those in the physical experiment,the components in the high frequency have obvious differences.
layered Boussinesq-type equation;deep water wave;numerical simulation
P731.22
A
1003-2029(2010)04-0109-04
2010-03-10
海洋公益性行业科研专项(200905002)
余向军(1982-),男,博士研究生,主要从事海浪理论方面研究。E-mail:xiangjun_yu@163.com

