半潜式平台完全时域耦合运动分析
元志明,嵇春艳,陈明璐
(江苏科技大学 船舶与海洋工程学院,江苏 镇江212003)
半潜式平台完全时域耦合运动分析
元志明,嵇春艳,陈明璐
(江苏科技大学 船舶与海洋工程学院,江苏 镇江212003)
采用三维频域GREEN函数法计算浮体的水动力特性,并运用非线性有限元法对系泊缆索进行模拟,通过完全时域耦合方法求解整个系泊系统的时域控制方程,得到半潜式平台系统的运动响应和系泊缆索的张力变化情况,并对这些响应结果的波频和低频成分进行了分离,讨论了各频率响应成分对平台系统运动的贡献。
半潜式平台;系泊缆索;非线性有限元;时域方法;耦合分析
引言
随着全球日益增长的能源需求以及浅水海域油气资源储量的逐渐减少,人们将目光投向了深海,尤其是水深超过3 000 m的海域。因此,适用于深海油气资源开发的浮式系统成为了研究的前沿领域。浮式系泊系统主要由三个部分组成:浮体、系泊缆绳和输油软管,除了浮体与系泊缆索之间复杂的相互作用外,系泊缆索的几何非线性以及作用于浮体上的拖拽力和二阶波浪力的非线性都使得时域的分析方法成为解决浮式系泊系统耦合问题的理想方法。传统的浮式系泊系统动响应的分析主要包括两个阶段[1]:第一阶段,运用绕射和辐射理论计算浮体的运动,在这一阶段的计算过程当中,将系泊缆索的影响视为线性的恢复力,涵盖于浮体的运动方程当中,运用频域方法便能对其进行求解;第二阶段,对系泊缆索进行动力分析,在这一阶段的分析当中,将第一阶段计算得到的耦合点(系泊缆索与浮体的连接点)的响应视为系泊缆索运动方程的上端边界条件,运用非线性有限元方法可以对其进行求解。这一方法忽略了作用在系泊缆索上的流载荷以及系泊缆索动力特性对浮体波频运动的影响,除此之外,系泊缆索的阻尼对浮体的低频运动也无法完全模拟[2]。随着水深的增加,系统的非线性愈加明显,因此,将浮体于系泊缆索独立开来分别进行求解的方法将无法保障浮式系统运动相应的精度。而随着计算机性能的快步提升,完全的时域耦合分析将变得可行,并能提高耦合分析的可靠性。
完全时域耦合分析将运用Wilson-theta隐式迭代方法[3],同时计算浮体和系泊缆索的运动响应。这样,浮体和系泊缆索之间复杂的相互影响将能够被完全模拟。Low,Y.M.和Langley,R.S.[4-5]运用完全时域方法,编写了浮式结构的耦合分析程序,并得到了令人满意的结果;由于时域迭代的方法计算时间较长,为了平衡精度和效率,文献[6-9]提出了一些有效的完全耦合计算方法。本文将完全时域方法运用于一半潜式平台,首先通过SESAM软件的GeniE建立该平台的有限元模型,并在HydroD中分析其水动力性能,得到平台的附加质量、附加阻尼和频响函数,最后在DeepC中求解整个系泊系统的时域耦合方程,计算分析其运动特性以及系泊缆索的张力情况,为深水半潜平台张紧式系泊系统设计提供参考。
1 浮体—系泊耦合运动方程
浮式系统耦合控制方程的时域形式可以表达为[10]:

式中:x(t)为系统的位移矩阵;M、C、K、F分别代表系统的质量、阻尼、刚度和外力矩阵;下标V和L分别表示浮体和系泊缆索。其中:

m为浮体的质量矩阵;μ为辐射势产生的附加质量矩阵;CV为辐射势产生的附加阻尼矩阵;系泊缆索对于阻尼和刚度矩阵的贡献包含于外载荷矩阵FL(t)当中,所以这两项均为零。
2 环境载荷计算
2.1 浮体的外载荷[10-13]
浮体的外载荷矩阵可以表达成如下形式:

式(3)中,Ffk为佛汝德—克雷洛夫力;Fd为波浪绕射力;Fw为风力;Fc为流力;Fsd为二阶漂移力。


式(4)-(8)中:φ0和φ7分别代表波浪的入射势和绕射势;p为风压;Vc为流速;Aw和Ac分别为受风和受流面积;Tsd为二阶传递函数;η(ωm)和 η(ωn)分别为两种频率的波的幅值。
2.2 系泊缆索的外载荷
浮体的外载荷矩阵可以表达成如下形式[10]:

式(9)中:T和Q为轴向和扭转恢复力;W为有效重力;FdL为拖拽力;FLI为惯性力;FLs为浮体与系泊缆索耦合点之间的相互作用力。拖拽力可以写成如下形式:

这里,

式中:D为缆索的外径;Lξ表示单元ξ的原始长度;CnD和分别表示法向和切向的拖拽力系数;u为流体质点的速度;tξ为单元ξ的单位切向向量。
惯性力可以写成如下形式:
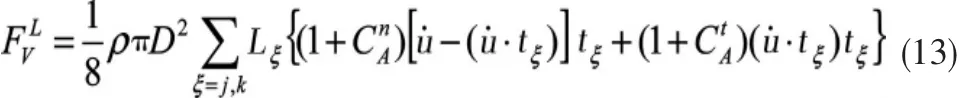
这里,CnA和ClA分别表示法向和切向的附加质量系数。
将式(3),(9)代入式(1),并采用 Wilson-theta[10]或者 Runge-Kutta[2]数值积分方法对其进行数值求解,从而得到浮式系泊系统的运动响应。
3 半潜式平台数值算例
3.1 半潜式平台概况
3.1.1 半潜式平台主要参数
运用上述理论将对一位于墨西哥湾的半潜式平台进行耦合分析。平台主要参数如表1所示。

表1 平台主要参数
3.1.2 系泊缆索主要参数
平台通过12根系泊缆索系泊于固定海域,具体布置如图1所示。系泊缆索两端采用钢链,中间段采用聚酯缆绳,两种材料的主要参数见表2。

图1 系泊缆索布置图

表2 系泊缆索主要参数
3.1.3 环境参数
本文选用墨西哥湾百年一遇的暴风条件作为其工作海况,波浪选用jonswap谱,有义波高取 12.19 m,周期14 s,入射角为90°(如图1所示);风谱选用API RP 2A-WSD谱,参考高度为10 m时风速41.12 m/s,方向210°;海面的流速为1.067 m/s,91.44 m 水深处为0.091 4 m/s, 海底0.091 4 m/s,方向150°。波浪的周期取的是1~38 s,步长为2 s,而对系统进行耦合分析时,采用的是时域方法,模拟周期为3 600 s,步长为 0.2 s。
3.2 仿真结果
运用GeniE建立该平台的有限元模型,然后在HydroD中分析其水动力性能,得到平台的附加质量、附加阻尼和频响函数,最后在DeepC中求解整个系泊系统的时域耦合方程,从而得到系泊系统的运动响应。
3.2.1 平台水动力系数
平台水动力的分析的重点在于附加质量和附加阻尼的求解,图2和图3为半潜式平台浮体的附加质量和附加阻尼。
3.2.2 系统的运动响应
在得到平台浮体的水动力系数之后,采用时域的耦合方法,对系统的运动方程进行求解。系统六自由度运动响应如图4(a)-(f)所示。

图2 (a)附加质量(A11,A12,A33)
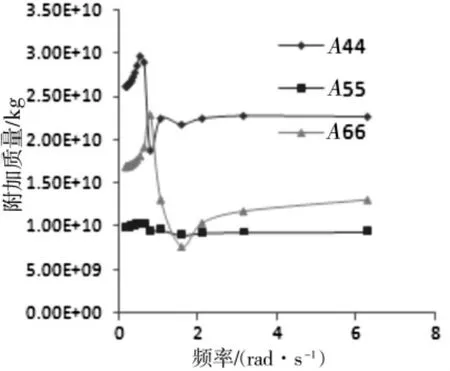
图2 (b) 附加质量(A44,A55,A66)

图3 (a)附加阻尼(D11,D12,D33)

图3 (b)附加阻尼(D44,D55,D66)

图4 (a)纵荡时间历程
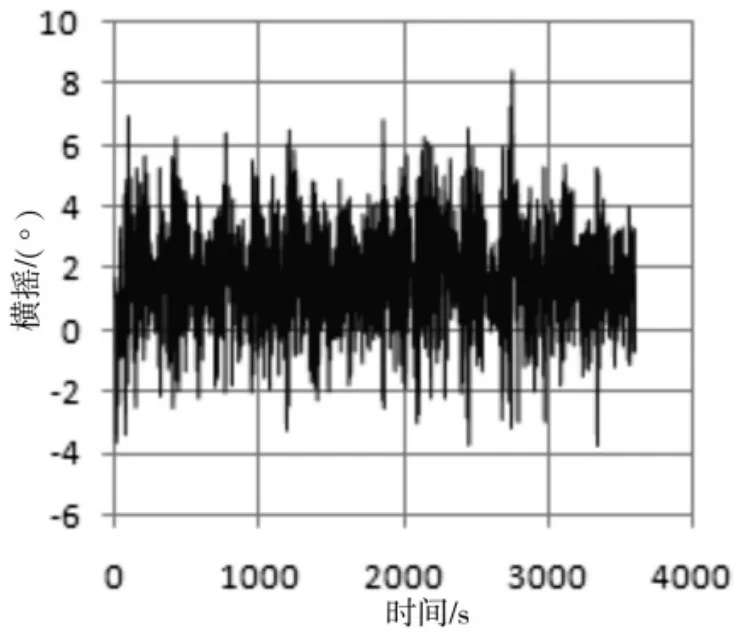
图4 (b)横摇时间历程
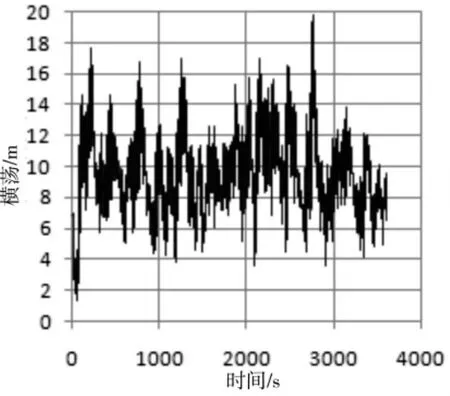
图4 (c)横荡时间历程
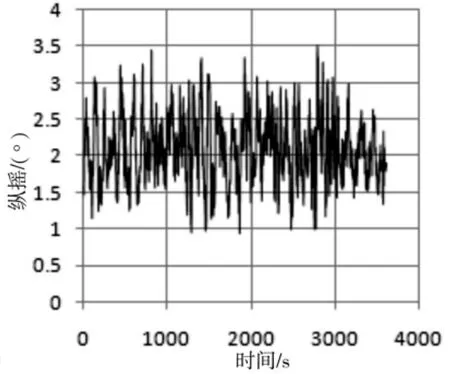
图4 (d)纵摇时间历程
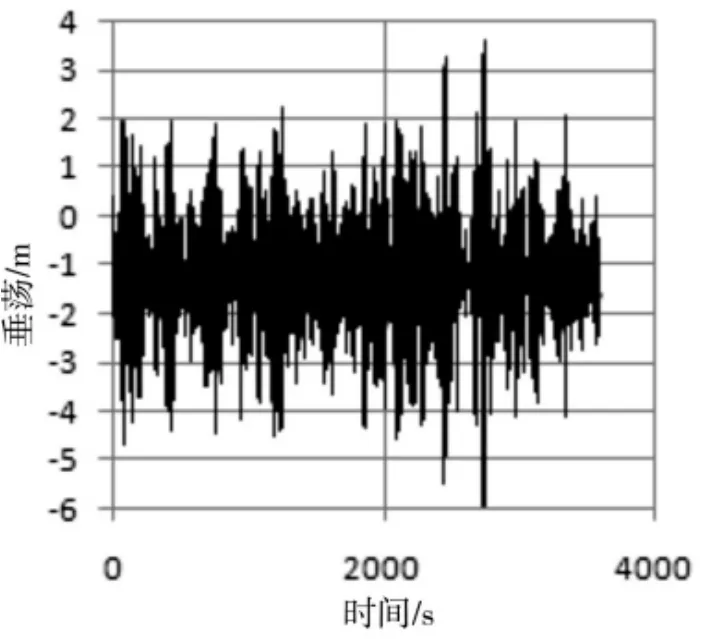
图4 (e)垂荡时间历程

图4 (f)首摇时间历程
由系统六自由度运动的时间历程可以看出,在三种平移自由度当中,纵荡和横荡运动的运动幅值最大;同时,在三种旋转运动当中,首摇最为激烈,这除了与结构自身的特征有关外,入射波及风流的角度也是其中的原因之一。
通过对上述时域信号进行傅里叶变换,获得结构运动响应的频域曲线,如图5所示。
图5(a)~(d)反映了各频率对系统运动的贡献。在研究浮式系统的耦合运动响应时,除必须考虑浮体与系泊缆索之间的相互影响外,系统的低频运动(LF)(0.02 rad/s附近)和波频运动(WF)(0.2~2 rad/s)之间的耦合也是研究的重要内容。为了直观反映系统低频和波频响应,可将低频和波频成分分离开来,并定义低频响应的频率区间为0~0.2 rad/s,波频响应的频率区间为0.2~1.2 rad/s。以纵荡运动为例,其低频和波频响应的时历曲线如图6所示。

图5 (a)纵荡、横荡运动谱密度
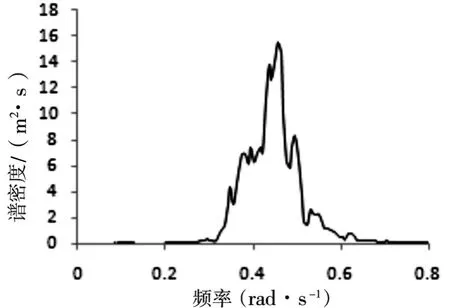
图5 (b)垂荡运动谱密度
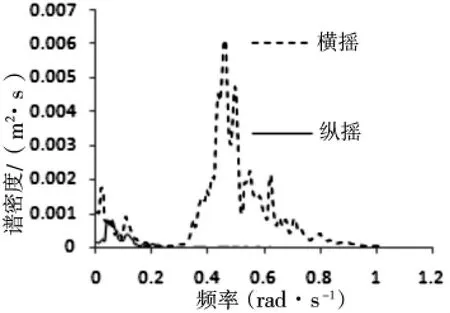
图5 (c)纵摇、横摇运动谱密度

图5 (d)首摇运动谱密度
由图6(a)~(b)可以发现,纵荡低频运动的响应幅值远大于波频运动的响应幅值,这一特征也可以从图5(a)中看出,整个频率范围内,0~0.2rad/s的贡献占据主导地位。除此之外,从图5中亦能看出,横荡、首摇和纵摇运动时,低频亦起着主要作用,而横摇和垂荡则主要是波频响应的贡献。现将所有自由度运动的低频和高频进行分离,并将主要结果归纳为表3。
3.2.3 系泊缆索的响应
除系统六自由度响应外,系泊缆索的受力情况也是耦合分析的重点。图7为系泊缆索1的静力分析结果,图8为系泊缆索10靠近导缆孔(第一个单元)处张力的时历曲线:
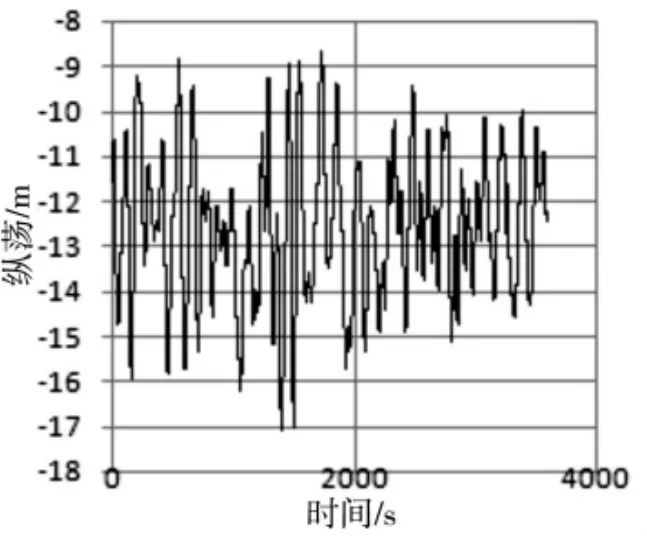
图6 (a)横荡低频响应

图6 (b)纵荡波频响应

表3 系统六自由度响应结果

图7 缆索1有效张力
由图7可以看出,系泊缆索的有效张力随着其向海底延伸而逐渐变小,由于0~152 m及1 642~1 733 m长度为钢链,因此张力变化要比聚酯缆大。靠近上端导缆孔处达到最大值,因此,图8给出了这一位置单元张力随时间变化的曲线。

图8 缆索10张力时间历程
将所有系泊缆索的第一个单元张力的时间历程进行汇总,可以得出其有效张力的计算结果。
由表4可以看出,10#系泊缆绳受到的有效张力是最大的,极值为2 012 kN,以破断载荷除以该值,便可以得到此时的安全系数为4.4。根据API RP 2SK设计规范,使用动力分析计算时,钢链、钢缆最大张力的安全系数取1.67,故设计合理。

表4 系泊缆索张力的计算结果
4 结语
采用时域耦合方法,得出了半潜式海洋平台的运动响应,并求得其系泊缆索的张力变化。计算结果表明,系统六自由度运动响应以纵荡和横荡的运动幅值最大,同时,将这些运动中的低频和波频成分分离出来后发现,平台在水平平面内的运动(纵荡、横荡和首摇)以低频成分占主导地位,而波频成分在平台垂直平面内的运动(垂荡、纵摇和横摇)发挥更大的作用。此外,系泊缆绳的有效张力随着水深的增加而减小,变化的曲率与系泊缆索的材质有关。
[1]Y M Low,R S Langley.A simplified model for the study of dynamic coupling effect in deepwater floating structures[C]//OMAE 2005-67062,24th International Conference on Offshore Mechanics and Arctic Engineering,Halkidiki,2005.
[2]DeepC User Manual,DNV Software,2005.
[3]Clough RW,Penzien J.Dynamics of structures.2nd ed.McGraw-Hill,1993.
[4]Low Y M,Langley R S.A comparison of time domain and frequency domain approaches for the fully coupled analysis of deepwater floating structures[C]//Proc Conf Offshore Mech Arctic Eng,2006.
[5]Low Y M,Langley R S.Dynamic analysis of a flexible hanging riser in the time and frequency domain[C]//Proc Conf Offshore Mech Arctic Eng,2006.
[6]Ormberg H,Larsen K.Coupled analysis of floater motion and mooring dynamics for a turret-moored ship[J].Applied Ocean Research,1998,20(1-2):55-67.
[7]Chaudhury G,et al.Coupled dynamic analysis of platforms,risers,and moorings[C]//Offshore Tech Conf,2000.
[8]Kim S,Sclavounos P D.Fully coupled response simulations of theme offshore structures in water depths of up to 10,000 feet[C]//Offshore Tech Conf,2001.
[9]Senra S F,et al.Towards the integration of analysis and design of mooring systems and risers,Part II:Studies on a DICAS system[C]//Proc Int Conf on Offshore Mech and Arctic Eng,2002,1:291-298.
[10]Y M Low,R S Langley.Time and frequency domain coupled analysis of deepwater floating production systems[J].Applied Ocean Research,2006,(28):371-385.
[11]肖越.系泊系统时域非线性计算分析[D].大连:大连理工大学,2005.
[12]戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.
[13]陈新权.深海半潜式平台初步设计中的若干关键问题研究[D].上海:上海交通大学,2007.
Full Time Domain Coupled Analysis of Semi-submersible Platform
YUAN Zhi-ming,JI Chun-yan,CHEN Ming-lu
(Institute of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)
3D Green’s function in frequency domain is adopted to calculate the hydrodynamic characteristics of the platform.The mooring lines are simulated using non-linear finite element method.After solving the equations of motion of the entire floating system by employing full time domain coupled analysis method,the platform’s motion response and lines’ tension are obtained.Furthermore,wave frequency response and the low frequency response are separated before a further discussion of the effect of these compositions to the platform system.
semi-submersible platform;mooring lines;non-linear finite element;time domain;coupled analysis;
P75
A
1003-2029(2010)04-0081-07
2010-06-20
国家自然科学基金资助项目(51079065)

